Valoración de Inversiones Financieras

ASIGNATURA: ESTRATEGIAS DE INVERSIÓN

TRABAJO N° 2. Modelos de Valoración de Activos Financieros

Autor: Alis Chavela Fernández Torres

Introducción

La estructura de capital o endeudamiento de una empresa determina el orden preferente de financiación de sus niveles de inversión. Por otra parte, quien posee los títulos valores diversificará de tal modo su cartera de activos con la finalidad de obtener el menor riesgo para cada nivel posible de ganancia.

En el proceso de valoración de activos financieros se pueden utilizar muchos modelos, dependiendo del sujeto que valora y la finalidad con que lo hace.

Con independencia de modelo que se utilice, en todo proceso de valoración, se necesitan fuentes de información lo más objetivas posibles, a fin de comparar con un eventual precio de mercado el valor que éstos pueden tener para cada sujeto decisor, ya sea en mercados organizados o en la negociación privada.

En el siguiente texto se tratará sobre los diferentes modelos que pueden ser utilizados para la valoración de activos financieros, ya sean solos o en una cartera de inversión.

1. Rentabilidad

Es la relación que se establece entre lo que se ha invertido en una determinada acción y el rendimiento económico o resultado que proporciona. El rendimiento que un accionista puede obtener de una acción se mide computando los dividendos percibidos, las plusvalías o revalorizaciones en su cotización, así como las ventajas que puedan obtenerse por el carácter preferente de las ampliaciones de capital vía derechos de suscripción preferente.

La rentabilidad de un valor i en un período de tiempo t vendrá definida por la relación:

Donde:

P_i,t, P_{i, t-1}Precios al principio y al inicio del período

R_i,tRentabilidad expresada en tanto por uno

D_i,tDividendos y derechos repartidos en el período t

Esta rentabilidad a posteriori, R_i,t , es una magnitud conocida con certeza. Sin embargo, a priori, se trata de una variable aleatoria de carácter subjetivo que depende de nuestras expectativas. Como variable aleatoria podrá tomar distintos valores, con unas probabilidades determinadas. Otra forma de proyectar la rentabilidad esperada de una acción es utilizar un promedio histórico de las rentabilidades ocurridas en el pasado.

2. Riesgo

En inversiones, hablar de riesgo se refiere a las posibilidades que existen de no obtener el retorno esperado de una inversión, siendo en este caso afectados por un evento fortuito que podría hacer que el inversionista pierda parte o la totalidad de lo que ha invertido. Hay riesgos de perder los ahorros, también riesgo de retraso en los plazos previstos, etc. Sin embargo, existen métodos para disminuir el riesgo, y éstos se basan en el conocimiento del riesgo intrínseco que existe en cada inversión antes de llevarla a cabo.

Las principales fuentes de riesgo son:

Riesgo de Mercado: este tipo de riesgo afecta a todos los inversionistas debido a que los factores de riesgo que lo componen están presentes en mayor o menor medida en las operaciones que realizan. Los factores de riesgo de mercado básicamente son las tasas de interés, tipos de cambio, valor de los activos bursátiles como las acciones, y el valor de bienes físicos como metales preciosos y productos agrícolas.
Riesgo de Liquidez: se representa cuando la institución carece de recursos o no cuenta con las condiciones para contraer pasivos bajo condiciones normales. Los problemas que conforman el riesgo de liquidez son la pérdida potencial por la venta anticipada o forzosa de activos a descuentos inusuales para hacer frente a obligaciones contraídas, así como la pérdida potencial por no contar oportunamente con recursos para enajenar, adquirir o cubrir una posición contraria.
Riesgo de Crédito: está definido como la pérdida potencial debido al incumplimiento de las obligaciones de las contrapartes.
Riesgo Operativo: es la pérdida potencial por fallas o deficiencias en los sistemas de información, en los controles internos o por errores en el procesamiento de las operaciones. NO ES CUANTIFICABLE, sin embargo, existen una serie de medidas que ayudan a su control y disminución.
Riesgo Legal: es la pérdida potencial por incumplimiento de las normativas legales y administrativas aplicables a las operaciones que las instituciones llevan a cabo.

El riesgo o volatilidad de un activo financiero se mide por la dispersión de sus posibles resultados. Cuantitativamente, el riesgo se representa con la varianza o con la desviación estándar. Dada una determinada rentabilidad, cuanto mayor sea la desviación estándar, mayor será el riesgo.

3. Análisis de Portafolios

Una cartera de valores o portafolio es una combinación de valores mobiliarios (acciones, bonos o dinero).

Para el análisis de portafolios se necesita:

ò El rendimiento esperado de cada título que es candidato a formar parte del portafolio

ò La varianza de cada título

ò La covarianza entre cada par de instrumentos

El análisis de portafolios requiere valuar la correlación entre cada par de títulos que funcionen como candidatos para su inclusión en el portafolio.

La rentabilidad de una cartera o portafolio es igual a la media ponderada de las rentabilidades de los activos que la componen. Se ponderan las rentabilidades. Se ponderarán las rentabilidades por el peso específico que cada activo tiene en la cartera.

E(R_p) = w_1
*E(R₁) + w_{2 *}E(R₂) + ..... + w_{n *}E(R_n)

En donde:

E(R_p) Rentabilidad esperada de la cartera

W_n Porcentaje de la cartera (en tanto por uno) invertido en cada acción.

E(R₁) Rentabilidad esperada de cada acción que entra en la cartera.

Ejemplo:

Acción	Peso	Re
A	0,4	9,20%
B	0,6	5,50%
Cartera A-B		6,98%

R_Cartera
A-B= (0,4*9,20%) + (0,6*5,50%) = 6,98%

El riesgo dado por una cartera formada por dos valores viene dado por la expresión:

s ²_p= w ²_a*s ²_a+ w ²_b*s ²_b+ ..... + 2 w_a* w_b * Cov _a,b

La covarianza nos dice en qué medida dos acciones se mueven en el mismo sentido; si la covarianza es positiva, quiere decir que cuando la rentabilidad de una acción sube, la de la otra también sube; si la covarianza es negativa, quiere decir que cuando la rentabilidad de A sube, la de B baja. Si la covarianza es próxima a cero, quiere decir que las dos acciones son independientes.

Un parámetro estadístico que nos indica la relación entre dos acciones es el coeficiente de correlación r. Este coeficiente viene dado por la siguiente fórmula:

r_ab = Cov _ab

s_as_b

Como el rendimiento esperado de una cartera es siempre la media ponderada de los rendimientos de sus componentes, mientras que la desviación estándar es menor que la media ponderada de las desviaciones de sus componentes en el caso de carteras con activos que no estén perfectamente correlacionados, siempre tendremos una combinación rentabilidad/riesgo mejor que cualquier valor tomado individualmente.

3.1. Teoría de Markowitz

Markowitz elaboró un modelo para la obtención de una cartera óptima, considerando la conducta racional del inversor, que consiste en maximizar el rendimiento esperado y minimizar el riesgo. La cartera óptima es aquella que permite la mejor combinación de rentabilidad y riesgo dentro de los activos disponibles en el mercado.

Markowitz muestra cómo puede reducirse el riesgo de total de una cartera de inversión combinando activos financieros cuyos rendimientos no se vean afectados de la misma manera por los factores que producen variaciones en los mismos.

En su modelo ahora son fundamentales las siguientes premisas:

1. Un inversionista puede estimar la rentabilidad y su distribución de probabilidad para toda acción o cartera de inversión

2. La media de esa distribución representa su rentabilidad esperada

3. Su varianza o desviación estándar representa el riesgo de la acción o cartera

4. Es preferible un título o cartera con una mayor rentabilidad y menor riesgo

5. Es eficiente una cartera que ofrece la mayor rentabilidad para un nivel de riesgo dado

6. Es óptima para cada inversionista la cartera que se encuentra en el punto de tangencia entre el conjunto de carteras eficientes y una de las curvas de indiferencia para el inversionista

El valor relevante propuesto por Markowitz es la covarianza entre cada par de títulos. En este contexto, la covarianza es el coeficiente de correlación entre los cambios de los precios de dos acciones multiplicado por el producto de sus desviaciones estándar. Entonces las bajas covarianzas corresponderán a títulos con desviaciones estándar pequeñas o, sobre todo, con una baja correlación en los cambios en sus precios; por lo tanto, deben buscarse acciones con bajas covarianzas para incorporarlas a una cartera de inversión y reducir el riesgo total.

Markowitz llamó carteras eficientes a las que proporcionan los rendimientos esperados más altos para cada nivel de riesgo, o el menor nivel de riesgo para cada rendimiento esperado.

Las alternativas para integrar una cartera no se limitan a los títulos de renta variable. Muchos administradores de carteras de inversión las configuran con una mezcla de acciones y bonos. De acuerdo al análisis de cartera de Markowitz, se define el conjunto de mezclas óptimas entre renta fija y renta variable como el conjunto de estrategias dominantes que minimizan el riesgo para cualquier nivel de rendimiento.

Los trabajos de Markowitz tienen una continuación natural en las aportaciones de Sharpe, Lintner y Treinor, quienes introducen el C.A.P.M. (Capital Asset Pricing Model) , auténtico modelo de equilibrio para el comportamiento de los mercados de capitales. El CAPM es extendido por Ross hasta los modelos A.P.T. (Arbitrage Pricing Theory) y sienta las bases de lo que será la valoración por arbitraje, auténtica piedra angular para la teoría de activos financieros, especialmente activos derivados.

La rentabilidad de un valor mobiliario esta afectado por dos tipos de riesgos: Un riesgo propio o "especifico" que depende de las características especificas de la entidad o empresa emisora, naturaleza de sus actividad productiva, competencia de la gerencia, solvencia financiera etc. y este tipo de riesgo también se le conoce como "no sistemático o no diversificable" y un segundo tipo de riesgo, llamado "Sistemático o de Mercado", que no depende de las características individuales del titulo, sino de otros factores (coyuntura económica general) que inciden sobre el comportamiento de los precios en el mercado de valores. A este segundo tipo de riesgo también se le denomina como "No Diversificable", ya que no será posible eliminarlo mediante la diversificación, dada la correlación existente entre la rentabilidad del titulo en cuestión con las rentabilidades de otros títulos a través del Índice Bursátil que resume la evolución del mercado.

3.2. Teoría del equilibrio de mercados

La Teoría del equilibrio en el Mercado de Capitales es una extensión del modelo de Markowitz y consiste en introducir la posibilidad de que el inversor no invierta todo su presupuesto en activos con riesgo, sino que una parte del mismo la dedique a la adquisición de activos sin riesgo o bien lo ceda en préstamo al tipo de interés de dicho activo sin riesgo.

Al incluir la posibilidad de prestar (o pedir prestado) una parte del presupuesto de inversión, la curva de carteras eficientes del modelo de Markowitz se convierte en una recta. La cartera estará formada ahora por dos tipos de activos: Un activo sin riesgo que será la parte prestada (o adeudada) y un activo con riesgo, concretado en un valor mobiliario o combinación de varios valores mobiliarios (cartera), perteneciente a la frontera eficiente original, generada conforme a la lógica del modelo de Markowitz, cuando no se había tenido en cuenta la existencia de activos sin riesgos.

3.3. Modelo Capital Asset Pricing Model (C.A.P.M.)

El modelo expone que la tasa de actualización k o rendimiento requerido, que se utiliza para actualizar el flujo de fondos esperados FFD es una función de la tasa de interés sin riesgo R_f y del adicional por riesgo de mercado MRP ponderado por la sensibilidad beta b del negocio al mercado de títulos.

K_j = R_f + MRP * b_j

MRP (Market Risk Premiun) es la diferencia entre el rendimiento esperado de la cartera del mercado (que representa a los títulos con riesgo) y la tasa de interés sin riesgo.

MRP = R_m- R_f

En C.A.P.M. se considera que la tasa de interés sin riesgo R_fes la tasa de rendimiento de un titulo para el que no se percibe riesgo de incumplimiento de los servicios estipulados. Habitualmente se considera como estimación de la tasa sin riesgo el rendimiento de los títulos del gobierno.

Los rendimientos de los bonos son libres de riesgo en términos nominales, no en términos reales. Se suele utilizar la tasa expresada en términos “nominales” (incluyendo la inflación) que se espera para el período futuro relevante de la valuación, cuando la inflación es baja y relativamente estable.

El factor Beta (b) es la medida de la volatilidad de un activo. Es un coeficiente que muestra cuán sensible es una acción a las fluctuaciones del mercado.

Valor de b	Significado
b = 1	Para una sola acción: es una acción típica o de riesgo promedio. Tiende a variar en la misma medida y dirección del mercado. Para una cartera: la cartera es tan volátil como el mercado, tiende a variar en la misma medida y dirección que el mercado. Puede ser la cartera del mercado
b > 1	Para una acción: Es una acción más volátil que el mercado. Tiende a variar más que el promedio del mercado y en la misma dirección. Esto puede ocurrir con una acción especulativa con tendencia procíclica. Para una cartera: la cartera es más volátil que el mercado. Esto puede ocurrir con una cartera de acciones especulativas con tendencias procíclicas ( sea que depende mucho de los ciclos del mercado).
b < 1	Para una acción: Es una acción menos volátil que el mercado. Tiende a variar menos que el promedio del mercado y aunque en la misma dirección. La acción puede tener características propias que la hacen más riesgosa. Para una cartera: Es una cartera menos volátil que el mercado. Tiende a variar menos que el promedio del mercado y aunque en la misma dirección. Esto puede ocurrir si se combinan acciones pero que al diversificar elimino el riesgo particular dejando bajo el riesgo del mercado.
b = 0	Implica que un título no depende en lo absoluto de lo que pasa en el mercado. Suele ser un título libre de riesgo como los bonos del tesoro.
b < 0	Es muy raro para una acción. Implica que la acción o la cartera tiende a moverse en sentido contrario al mercado.

Lo normal es asumir que el coeficiente beta que ha tenido una acción en el pasado reciente es la que va a tener en el futuro próximo. El beta en el pasado reciente se calcula por medio de una regresión, utilizando datos históricos de las primas de riesgo de la acción y del mercado durante, por ejemplo, los últimos cinco años, pero no más de diez. Para estimar la rentabilidad futura de la acción, se utilizará el beta calculado y una estimación de la prima de riesgo de mercado.

El C.A.P.M. es válido para explicar el rendimiento requerido cuando los mercados financieros están integrados. En el caso de mercados emergentes, como Venezuela, que están poco integrados al mercado financiero global se plantea que para valuar negocios debe utilizarse una tasa ajustada por el mayor riesgo, ya que buena parte del riesgo en estos mercados no puede diversificarse financieramente.

3.4. Modelo de Valoración por Arbitraje

El modelo "Arbitrage Pricing Theory" (APT) fué propuesto por Stephen A. Ross en 1976. Según este modelo, una cartera o portafolio óptimo está constituido por aquellos valores que proporcionan un rendimiento máximo para el riesgo soportado, definido éste por su sensibilidad a los cambios económicos inesperados, tales como los cambios imprevistos en la producción industrial, en el ritmo de inflación y en la estructura temporal de los tipos de interés.

Este modelo comienza suponiendo que la rentabilidad de cada acción depende en parte de factores o influencias macroeconómicas y en parte de sucesos que son específicos de esa empresa; sin embargo, no establece cuales son esos factores.

3.5. Modelo de Mercado

En el modelo de mercado, a diferencia del CAPM, la rentabilidad de la acción depende directamente de la rentabilidad del mercado:

r_f= a + b * r_m+ e

El beta del modelo de mercado es el mismo que del C.A.P.M. La diferencia, desde el punto de vista de los resultados, está en el coeficiente alfa. Los coeficientes alfa y beta se calculan por regresión con datos históricos de la rentabilidad de la acción y la de un índice bursátil.

3.6. Modelos Multifactoriales

En los modelos multifactoriales, la variable explicada o dependiente es la rentabilidad de la acción. Las variables explicativas o independientes pueden ser, además de la rentabilidad del mercado, por ejemplo: el PER de la acción, la rentabilidad por dividendos, el nivel de endeudamiento de la empresa, el ratio valor de mercado/valor contable de la acción, los tipos de interés esperados, etc. En general, cualquier variable que se intuya que pueda tener influencia en la rentabilidad de la acción.

r_s = a + b_1
*x₁ + b_2
*x₂+ b_3
*x₃+ .... + b_n
*x_n + e

En donde:

r_sRentabilidad o variable explicada

x₁... x_nVariables explicativas

a Término independiente de la regresión

b₁... b_nCoeficientes de las variables explicativas

e Errores

Según este modelo, el precio de un activo financiero no sólo debe reflejar la prima de riesgo de mercado, sino también la prima de riesgo de factores extramercado.

4. Valoración de acciones

Una acción es un título que representa una parte del capital social de una empresa y que es colocado entre el público inversionista para obtener financiamiento. La tenencia de las acciones otorga a sus compradores los derechos de un socio.

Se pueden identificar varios tipos de acciones:

ò Acciones preferidas

Acciones que brindan a su poseedor prioridad en el pago de dividendos y/o reembolso del capital en el caso de disolución de la empresa. No dan derecho a voto en las asambleas de accionistas.

ò Acciones cíclicas

Acciones de empresas cuyas ganancias tienden a variar con el desempeño de la economía. Sus precios suben en presencia de un período económico favorable, y descienden ante una recesión. En ocasiones la fluctuación de estas acciones es característica para todo el sector o industria al que pertenezcan. Por ejemplo, la industria de acero, química, papel, automotriz, etc.

ò Acciones comunes u ordinarias

Acciones que otorgan a su tenedor derecho a voto en las asambleas de accionistas, derecho al cobro de dividendos y, en caso de liquidación de la empresa, el derecho sobre el balance de los activos una vez canceladas las acreencias y pagado a los accionistas preferentes.

ò Acciones de crecimiento

Acciones de compañías que se caracterizan por su gran potencial de crecimiento para el futuro. Son compañías generalmente innovadoras o agresivas. Estas empresas tienden a reinvertir las ganancias obtenidas con vista a una mayor expansión futura, por lo que no suelen pagar dividendos o lo hacen en muy poca cantidad.

4.1. Análisis Fundamental (bottom up)

El precursor del análisis fundamental fue Benjamin Grahan, cuya escuela de pensamiento se impuso entre todos los gestores de inversión de los años cincuenta y sesenta.

Consiste en valorar las acciones y comparar el precio resultante del análisis con el precio de mercado, buscando encontrar acciones minusvaloradas, que constituirán, según nuestro análisis, una buen oportunidad de inversión.

E1 valor de una acción es el valor de la empresa dividido por el número de acciones. Se busca saber si el precio de mercado de la acción refleja el valor y las perspectivas de la empresa. El valor no debe confundirse con el precio, que es la cantidad a la que el vendedor y comprador están dispuestos a realizar una operación de compra y venta de una empresa, y que puede no coincidir con el valor que ha determinado la valoración.

El valor de un titulo en el mercado está dado por el valor actualizado de los flujos de caja que origina la inversión en dicho titulo, ajustando la tasa de descuento de dichos flujos a las características de riesgo propias del titulo y demás circunstancias del mercado financiero, tales como la inflación, etc..A este valor teórico de titulo se le denomina valor intrínseco.

4.1.1. Métodos basados en el Valor Patrimonial

Consideran que el valor de una empresa radica fundamentalmente en su balance.

4.1.1.1. Valor contable

También conocido como valor en libros o patrimonio neto de una empresa, es el valor de los recursos propios que aparecen en el balance. De este concepto surge el valor contable teórico de una acción, también llamado Valor Patrimonial Proporcional, que resulta de dividir el patrimonio neto de la empresa por el número de acciones ordinarias emitidas.

4.1.1.2. Valor contable ajustado

Consiste en valorar cada una de las partidas del balance a su precio de mercado. La diferencia entre el valor de mercado del activo y el del pasivo da el valor contable ajustado. Trata de salvar el inconveniente de aplicar criterios exclusivamente contables en la valoración.

4.1.1.3. Valor de liquidación

Es el valor de una empresa en caso de liquidación, es decir, que se vendan sus activos y se cancelen sus deudas. Se calcula deduciendo del patrimonio neto ajustado los gastos de liquidación del negocio (indemnizaciones a empleados, gastos legales, gastos fiscales y otros gastos propios de la liquidación).

4.1.2. Métodos basados en ratios búrsatiles

Estos métodos se basan en la cuenta de resultados de la empresa y son muy usados en la valoración de acciones en bolsa. Tratan de determinar el valor de la empresa a través de la estimación de su rentabilidad futura.

4.1.2.1. Price Earning Ratios (PER)

También llamado ratio precio-beneficio de una acción indica el múltiplo del beneficio por acción que paga la bolsa.

Precio por acción PPA

PER = -------------------------------------- = ---------

Beneficio por acción BPA

Una vez comparada con registros históricos y con los niveles del mercado y de empresas similares es posible determinar si una acción está cara o barata. El PER de una acción debe ser coherente con el PER de las empresas del mismo sector y con las características de la empresa.

Una primera aproximación a cuál es el PER adecuado para una determinada acción es utilizar el PER como el inverso de la rentabilidad:

PER = 1/Rentabilidad = 1/R_f

Donde:

R_fTasa de Interés sin riesgo

Otro elemento importante es el crecimiento esperado de los beneficios futuros. Si los beneficios futuros crecen a una tasa g, el precio de la acción debería ser mayor y, por tanto, su PER será mayor.

PER = -----------------------

k - g

Donde:

k Rentabilidad que se le pide a la acción

g Tasa de crecimiento de los beneficios

A su vez, el crecimiento de los beneficios g depende de la rentabilidad sobre recursos propios (ROE) y del porcentaje de beneficios distribuidos como dividendos o pay out.

El valor del PER depende de las siguientes magnitudes: rentabilidad libre de riesgo, prima de riesgo exigida a las acciones, rentabilidad de los recursos propios, crecimiento esperado de la empresa, pay out o porcentaje de los beneficios que se reparten vía dividendos.

4.1.2.2. Valor de los dividendos

La rentabilidad por dividendo es el cociente entre el dividendo esperado para el próximo año y el precio de la acción hoy,

Rentabilidad por dividendos = DPA / P

Donde:

DPA Dividendo por acción

P Precio por acción

4.1.2.3. Multiplos de las ventas

Este método de valoración consiste en calcular el valor de una empresa multiplicando sus ventas por un número.

Precio

----------------------- = PER * Rentabilidad sobre ventas

Ventas

4.1.3. Métodos basados en el descuento de flujos de fondos

Tratan de determinar el valor de la empresa a través de la estimación de los flujos de dinero (cash flows) que generará en el futuro, para luego descontarlos a una tasa de descuento apropiada según el riesgo de dichos flujos.

4.1.3.1. Metodología para el descuento de flujos

La valoración por medio del descuento de flujos parte de la idea del valor del dinero en el tiempo, el valor futuro (VF) el año que viene de un peso es igual al valor presente hoy (VP) multiplicado por 1 más la rentabilidad que esperamos (K):

VF = VP * (1+K)

Si se introduce el factor “riesgo”, ya no se tendría la seguridad de recibir ese valor futuro, y seguramente se preferiría recibir el valor presente hoy, salvo que ses ofrezca una mayor rentabilidad. Por esta razón, cuando se ve incertidumbre, se utiliza una mayor tasa descuento K.

Si se quiere descontar un conjunto de flujos que serán recibidos en varios años:

CF₁CF₂ CF₃CF_n + V_n

V = ----------- + ----------- + ----------- + ..... + -----------------

(1+k) (1+k)² (1+k)³ (1+k)ⁿ

Donde:

V Valor de la empresa hoy

CF_i Flujo de fondos generado por la empresa en el período i

V_n Valor residual de la empresa en el año n

K Tasa de descuento

4.1.3.2. Determinación de la tasa de descuento

La tasa de descuento será mayor cuanto más inciertos sean los flujos de la empresa. Si no tuvieran ningún riesgo, se descontarían a la tasa libre de riesgo. Es decir, se le pide a la empresa una rentabilidad mayor que la rentabilidad libre de riesgo, que se llama prima de riesgo.

K = r_f + r_p

Donde:

K Tasa de descuento o rentabilidad que le pedimos a la empresa

r_f Rentabilidad libre de riesgo o rentabilidad de las letras del Tesoro

r_pPrima de riesgo que le pedimos a la empresa

4.2. Análisis Técnico

El "Análisis Técnico" es un conjunto de técnicas que pretenden predecir los precios bursátiles a partir de la evolución histórica, y del comportamiento de ciertas magnitudes financieras, como el volumen de negociación.

Un analista técnico, examina día a día la evolución de los precios de determinadas acciones, y del comportamiento de los precios en el pasado extrae conclusiones para el futuro. Se supone que los precios bursátiles describen trayectorias que de algún modo son repetitivas.

La base del análisis técnico es analizar el comportamiento del mercado según lo ocurrido en el pasado. Para ello se deben elaborar una serie de gráficos, que combinados con el volumen de negociación determinan el comportamiento futuro del mercado.

5. Valoración de Bonos

Un bono simple (straight bond) es un contrato que promete el pago periódico de un interés (cupón) por un determinado período, y el pago del principal al momento del vencimiento del período.

El más simple de los bonos es el bono de descuento o bono cero cupón. Este tipo de bono efectúa un solo pago, igual al principal (face value), al vencimiento.

El precio de un bono será igual a la suma del Valor Presente de todos los cupones más el Valor Presente del Valor Par del instrumento al vencimiento.

C C C C A

Valor del bono = ------------- + ------------- + ------------- + .........+ ------------ + ------------>

(1 + r)¹(1 + r)²(1 + r)³(1 + r)ⁿ(1 + r)ⁿ

Donde:

C: pago de cupón (efectivo)

r: Tasa de Interés periódica

A: Valor par del instrumento

n: Número de períodos

El valor par del instrumento A representa el 100% del valor del instrumento, es decir, el valor nominal del bono en el presente que debe reembolsarse en la fecha de vencimiento.

En la valoración de bonos, la tasa interna de retorno se conoce como Yield to maturity del bono, o YTM.

6. Caso práctico

Valoración de acciones

Empresa: Mercantil Servicios Financieros C.A.

MVZ.A Mercantil Servicios Financieros C.A. Clase A

Acciones en Circulación: 299.873.422

Últimos beneficios otorgados
Fecha	Monto Total Beneficios (Bs.)	Beneficios	Precio Ajustado
10/08/2004	2.398.987.376,00	8,00	2.462,00
10/05/2004	10.503.628.800,00	35,00	2.365,00

Precio actual (21-octubre-2004): 3.600,00

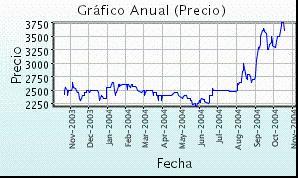
Como puede observarse en el gráfico anexo, el precio de estas acciones ha aumentado desde Julio 2004. Para ese mes tenía un precio aproximado de Bs. 2.500,00/acción, ubicándose en el precio de hoy en Bs. 3.600,00/acción.

Para esta acción el ratio precio – beneficio o PER será:

PER = Precio por acción / Beneficio por acción

PER = 2.462,00 / 8,00

PER = 307,75 (agosto 2004)

El valor de una acción viene dado por:

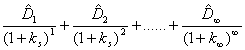
Donde:

D_t : Dividendo esperado por los accionistas al final de cada año

k: Tasa de rendimiento esperada que anticipa a un inversionista que compra una acción

Si se compra una acción el día 21-octubre-2004 su precio P₀ sería de Bs.3.600,00/acción. Suponiendo que en Agosto 2005 se reciba un dividendo con un crecimiento de un 5% con relación al dividendo recibido en Agosto 2004, este sería de Bs. 8,40/acción (D₁), se puede calcular el Rendimiento por dividendos esperados de la siguiente manera:

K_a = D₁/ P₀= 8,40 / 3.600,00 = 0,23%

Si observamos el gráfico de comportamiento de precios que va desde Octubre 2004 a Octubre 2005, el rendimiento de ganancias de capital para este período fue de:

g= P_{OCT 2004}– P_OCT2003= 3.600,00 – 2.500,00 = 0,30 = 30%

P_{OCT 2004} 3.600,00

Sí consideramos que esta sea una acción de crecimiento constante, la tasa esperada de rendimiento sería:

k_s = K_a + g = 0,23% + 30,00% = 30,23%

El valor de la acción será igual al valor presente de los dividendos obtenidos más el precio de la acción al final de ese año, de la siguiente manera:

Valor de la acción = D₁ + P_{1 .}

(1 + k_s)¹ (1 + k_s)¹

Donde P₁= P₀* (1 + g ) = 3.600,00 * 1,3 = 4.680,00

Valor de la acción = 8,40 / 1,3023 + 4.680,00 / 1,3023

Valor de la acción = 6,45 + 3.593,64

Valor de la acción = 3.600,00

Este resultado significa que el precio actual de la acción es el adecuado y, por tanto, vale la pena para el inversionista adquirir estas acciones.

7. Conclusiones

A fin de establecer un portafolio óptimo, el inversionista debe considerar formarlo con aquellos títulos que le den la mayor rentabilidad con el menor riesgo posible.

Para ello el inversionista debe realizar ciertos análisis que le permitan visualizarlo. Existen varios modelos que le permiten al analista de inversiones valorar su inversión.

El proceso de selección del método más apropiado, requiere el conocimiento acabado de los métodos, sus ventajas y debilidades, las características de una acción y su empresa, el mercado donde cotiza, etc..La selección de uno u otro modelo para estimar el valor más "razonable" surgirá de cada acción en particular y de cómo dicho activo está más o menos influenciado por las variables en que cada método se basa para estimar su valor.

Infografía