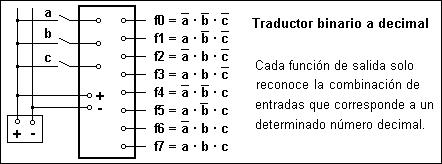

Funciones lógicas de base: Por compleja que pueda ser la lógica digital, solo está basada en tres funciones lógicas muy sencillas, a partir de las cuales se consiguen condiciones más complejas. Cualquier tecnología con elementos que funcionen según las tres funciones de base se puede aplicar en la resolución de automatismos. La función NOT es verdadera siempre que la variable a la que se aplica es falsa y será falsa en caso contrario. La función OR se aplica sobre dos o más variables y será verdadera siempre que alguna de las variables sea verdadera, será falsa cuando todas las variables sean falsas. La función AND también se aplica sobre dos o más variables y será verdadera siempre que todas las variables sean verdaderas, será falsa siempre que alguna variable sea falsa.
La función NOT o inversión se representa con una barra sobre la variable o condición a la que se aplica. La función OR se representa con el signo de la suma y la función AND se representa como un producto. Teniendo esto en cuenta ya debería deducir el significado de las funciones lógicas de la tarjeta de la máquina de refresco: Por ejemplo, la función f5 hace la operación AND con las tres entradas estando negada la "b", por lo tanto, es verdadera cuando estén accionados los captadores "a" y "c" y no esté accionado "b". Traducido a ceros y unos tendremos 101 que en decimal es el 5, luego la función f5 solo reconoce el decimal 5.
Experimente con elementos lógicos:
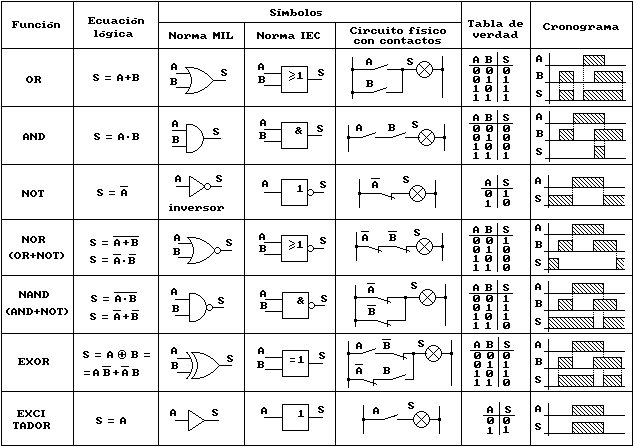
A continuación podrá experimentar el comportamiento de las principales funciones lógicas implementadas con esquemas de contactos y bloques lógicos. Por ser los más antiguos, los esquemas eléctricos fueron los primeros beneficiados de la lógica digital y es facil comprender su equivalencia con las funciones de base. Si ha experimentado con el ejemplo de la máquina de refresco, habrá visto cómo dos relés o contactores estaban encargados del accionamiento de un motor de corriente continua en sus dos sentidos de giro. Un relé o contactor cambia de estado unos contactos cuando recibe alimentación (continua o alterna) en su bobina, representada con un rectángulo y un trazo oblicuo en su interior. En esquemas lógicos, la bobina y los contactos de un relé no se representan juntos, con el fin de evitar cruces de líneas que dificultan la comprensión. Para que no haya duda sobre qué contactos corresponden a un relé determinado, se identifica la bobina y sus contactos con el mismo símbolo. Los esquemas de bloques se utilizan cuando la tecnología es neumática o electrónica. Por el momento nos basta con interpretar los bloques como elementos que reciben y transmiten señales de presión o tensión eléctrica.
Representación de funciones:
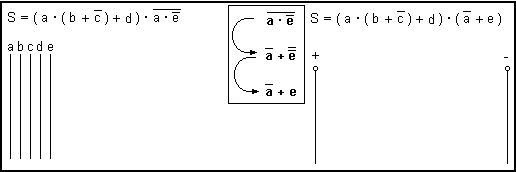
En la siguiente imagen vemos un ejemplo de función compuesta que se irá representando a medida que pulse el botón "adelante". Los productos, lo que está encerrado entre paréntesis y lo que está bajo el trazo de una inversión tiene más prioridad que las sumas, por lo tanto, no se debe representar una suma (operación OR) hasta no haber completado los términos con prioridad que van sumados. Para evitar errores, conviene comenzar a representar la parte más interna de la función (dentro de los paréntesis o bajo las barras de inversión) y cuando se completan dos términos con prioridad que van sumados, solo entonces se juntan sus terminales con bloque OR o se unen en paralelo (según se trate de bloques o contactos). Tenga en cuenta también que para representar con contactos las negaciones de sumas o de productos, lo mejor es aplicar los teoremas de Morgan (en el ejemplo se ha transformado la negación de un producto en una suma). Como la negación del producto es un término con prioridad, al transformarlo en una suma deberá mantener dicha prioridad, luego es fundamental encerrar la suma resultante entre paréntesis.
Aunque veremos más adelante recursos para facilitar la resolución de automatismos, siempre será bueno ejercitar una comprensión intuitiva de las funciones o relaciones lógicas: Para detectar errores y para resolver o simplificar casos sencillos sin recurrir a largos procedimientos de resolución. No debemos olvidar que sin intuición y experiencia seremos incapaces de interpretar porqué no funciona en la práctica lo que parecía perfecto en teoría. Si con experiencia se encuentran muchos contratiempos, sin experiencia se encuentran muchísimos más.
Las funciones lógicas se parecen mucho a nuestro lenguaje, por lo tanto, con un poco de práctica seremos capaces de "ver" en nuestra mente qué función o circuito resolvería un determinado automatismo solo con escuchar el planteamiento, siempre y cuando lo sepamos expresar de forma clara y simplificada. Supongamos un caso en el que un motor M deberá funcionar cuando se cumplan dos condiciones a la vez: Primera condición que esté pulsado alguno de los botones a y b y segunda condición que no esté accionado un interruptor c. Una descripción en términos lógicos sería la siguiente, en la que se obserba la equivalencia directa entre la función y la expresión que describe el problema:

El concepto "alguno" tiene equivalencia directa con: Suma lógica, bloque OR y contactos en paralelo.
El concepto "todos" tiene equivalencia directa con: Producto lógico, bloque AND y contactos en serie.
El concepto "no" tiene equivalencia directa con: Inversión lógica, bloque NOT y contacto normalmente cerrado.
Ejemplos neumáticos:
Durante años, la lógica neumática ha tenido una gran importancia en los sistemas que utilizan actuadores neumáticos (muy extendidos también en la actualidad). Modernamente, los autómatas programables están reemplazando casi por completo a los componentes lógicos neumáticos, excepto en aplicaciones donde las condiciones son extremas o existe grave peligro de incendio o explosión, como es el el caso de la automatización en pirotecnia.
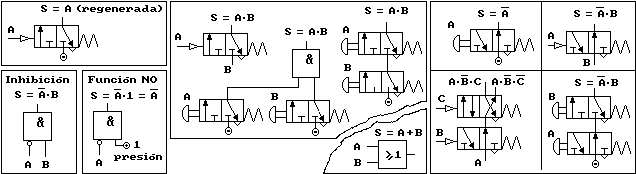
Los elementos de base Y, O, NO, etc., tienen equivalentes neumáticos que normalmente se conocen como módulo Y, módulo O, etc. Las señales de tratamiento son presiones que se transmiten a través de tubos de plástico flexible, resultando una lógica binaria a partir de la existencia o la falta de presión. Los módulos lógicos pueden reaccionar con una presión relativamente baja pero es habitual utilizar un valor de 6 bar, o bien de 4 bar solamente para la parte de mando. Las señales de salida de los módulos utilizan la misma presión que les llega por sus propias vías de entrada, hecho que puede hacer necesario regenerar la presión cuando la trayectoria seguida por una señal es muy larga o cuando circula en serie a través de muchos elementos.
El módulo inversor necesita una entrada de presión directa para poder transmitir una señal cuando no existe presión en su entrada negada. La función que realmente cumple el inversor se conoce como función inhibición. La realización práctica de una función Y también puede conseguirse mediante elementos en serie pero no es posible una función O mediante elementos en paralelo. La negación de una señal tampoco requiere necesariamente de un elemento inversor puesto que una válvula con una vía normalmente abierta permite dar una señal cuando no se acciona y la corta cuando sí se acciona.
Algunas posibilidades de formación de funciones básicas se pueden ver en las figuras. Otras funciones se forman agrupando adecuadamente varios elementos. Para ampliar información, consulte el tema de neumática.
Elementos lógicos en electrónica:
Existen diversas formas de construir componentes lógicos mediante transistores y diodos, pero se encuentran en el mercado circuitos integrados que incluyen determinado número de componentes lógicos ocupando un tamaño muy pequeño. El problema fundamental es que se necesita una alimentación de tensión estabilizada, frecuentemente debe construirse una placa impresa y las señales recibidas de contactos eléctricos originan efectos de rebote que exigen añadir elementos adicionales. Para ampliar información, consulte los temas de electrónica analógica y digital.