
1.- Comenzamos creando una tabla de la verdad con las variables del sistema y las funciones a resolver.
Las variables han sido denominadas c, b y a. Las funciones podemos llamarlas B para el relé izquierdo de bajada y S para el relé derecho de subiba. Para hacer referencia a combinaciones concretas de las variables podemos colocar a la izquierda el equivalente decimal, que se corresponde con el número de salida de la tarjeta de control. Representamos ya la combinación que aparece en condiciones de reposo:

El siguiente paso en la secuencia será poner un vaso para su llenado, hágalo pulsando el botón. La nueva combinación será:
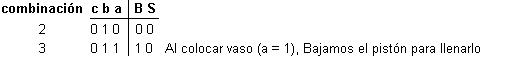
Por lo tanto, la combinación 3 debe hacer que baje el pistón. Conecte para ello la salida 3 de la tarjeta con el relé izquierdo de bajada (pulse primero la salida 3 y a continuación pulse la conexión del relé izquierdo). Si ya lo ha hecho, habrá visto que ha parado en cuanto comenzó a bajar porque ha cambiado la combinación:
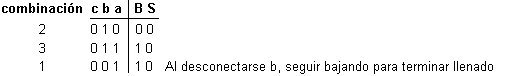
Para que siga bajando, conecte la salida 1 al relé izquierdo. Si ya lo ha hecho, se habrá llenado el vaso y estará parado por haber cambiado la combinación:

Ya puede retirar el vaso pulsando el botón. Si ya lo ha hecho, verá que ha cambiado de nuevo la combinación:
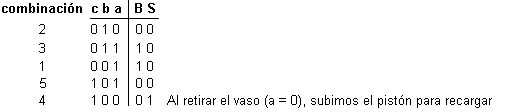
Conecte la salida 4 al relé derecho para que suba el pistón. Si ya lo ha hecho, se habrá parado nada más comenzar a subir, por haberse desconectado el captador inferior:

Conecte la salida 0 al relé derecho para que finalice la subida. Si ya lo ha hecho, verá que la combinación vuelve a ser la 2, que es la que existía en reposo. Por lo tanto, el ciclo ha terminado y pasaremos a resolver el problema basándonos en la tabla de la verdad. El número de combinaciones posibles con 3 variables es 8 pero solo se han necesitado 6, esto no es ningún problema porque ya están definidas las que deben activar las funciones B y S, no se necesitan las combinaciones con las que las funciones deben valer 0. En general, el número de combinaciones posibles es igual a 2 elevado al número de variables.
2.- Obtenemos las funciones lógicas de la tabla:
El automatismo simulado nos ha servido para detectar, paso a paso, las variables que van cambiando de estado. Pues bien, las salidas conectadas a cada relé definen la función correspondiente: Compruebe que el relé B de bajada se conecta con "alguna" de las salidas 1 o 3, es decir:
y que el relé S de subida se conecta con "alguna" de las salidas 0 o 4, es decir:
En la práctica, no tendremos una simulación que facilite las operaciones anteriores. Se necesita suficiente imaginación para ver mentalmente las sucesivas combinaciones que se van originando, cada vez que se produce un cambio de variable. Una vez creada la tabla de la verdad, ya es muy sencillo obtener las funciones:
Cada combinación es el producto lógico de todas las variables, poniendo negadas las que valen 0 y sin negar las que valen 1. Cada función es la suma de las combinaciones en las que la función vale 1.

3.- Simplificamos las funciones lógicas que se han obtenido:
Simplificar las funciones significa eliminar partes innecesarias para reducir el número de componentes que formarán el circuito de control. El siguiente cuadro contiene las reglas de simplificación que definen el llamado álgebra de Boole:
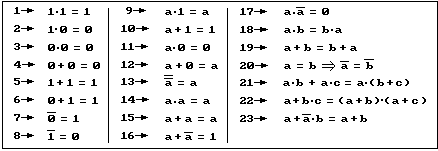
Sus demostraciones son sencillas si nos basamos en la tabla de la verdad, por ejemplo para la número 23 tendremos que los resultados para ambos lados de la ecuación son idénticos (resaltados en negrita), de modo que si ambos lados tienen el mismo valor para todas las combinaciones posibles, es que las dos cosas son equivalentes. Aunque no se ha indicado, es claro que lo contrario de 0 es 1 y viceversa.
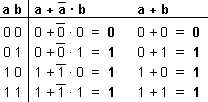
Para simplificar funciones, siempre buscaremos sacar factor común (regla 21) y obtener términos como indica la regla 16 (cualquier condición lógica sumada a sí misma pero negada es igual a 1). Las reglas más usadas son la 21 y 23. Veamos cómo lo podemos aplicar a las funciones de la máquina de refresco:

4.- Traducimos las funciones a la tecnología que interese:
La siguiente figura contiene la traducción de las funciones a esquemas de bloques y de contactos. La versión con contactos bien pudiera reemplazar a la tarjeta de la máquina de refresco, ya que solo se necesitan 2 funciones (los relés) y 4 contactos de los captadores para resolver el automatismo, mientras que la tarjeta precisa de 8 funciones y un gran número de contactos que no se necesitan. Como ventaja de la tarjeta, es que se puede utilizar para propósito general, siempre que no se necesiten más de 3 variables (con 4 variables asciende a 16 salidas, con 5 a 32 y así sucesivamente).
