Una sola cadena secuencial de 5 etapas es suficiente, por lo que puede comenzar introduciendo dicho número de etapas. Ajuste también el tiempo del temporizador, por ejemplo con 20 décimas de segundo (las unidades son décimas de segundo) y continúe rellenando las acciones de las etapas y las transiciones para el enunciado que a continuación se plantea:
Enunciado: Al colocar pieza sobre la cadena (se acciona V4) arrancará el motor S1 para llevarla hasta la posición de montaje detectada por V3. Una vez en posición, actuará el cilindro montador mediante la electroválvula S0. Cuando termina su recorrido de salida se accionará V1 y el conjunto estará montado, por lo que deberá retirarse el cilindro. Al accionarse V0, el cilindro estará retirado y el conjunto montado continuará su camino conectando de nuevo el motor S1. Con el motor funcionando, se repetirá automáticamente el proceso de montaje si continúan llegando piezas (si pulsa el botón que las pone junto a V4), pero si no llegan piezas en un tiempo superior al que haya ajustado en el temporizador, el motor se parará solo, entendiendo que se han terminado las piezas.
Programación de la cadena secuencial: En las etapas (campos de color blanco que aparecen pulsando al lado) puede activar las funciones escribiendo unos y desactivarlas con ceros. Por ejemplo, para conectar solo el motor S1 habrá que escribir 010, ya que el orden de introducción es S0 S1 S2. Las transiciones puede escribirlas en los campos de color azul claro, para lo que puede valerse del ejemplo explicado en el programa. En un solo campo de transición puede introducir varias condiciones de salto, separadas por una coma (no deje ningún espacio intermedio). Cada condición admite carga de estado de variables (solo el número, sin la letra V), operación OR con los dos últimos datos cargados (signo +), operación AND con los dos últimos datos cargados (signo *), negación del estado lógico resultante hasta encontrar el carácter de inversión (barra inclinada: /). Si la etapa en la que deberá continuar es la siguiente, no necesitará indicar ningún salto, pero si hay que saltar a otra etapa anterior o posterior habrá que añadir la letra S (mayúscula) y el número de etapa a la que saltará.
Una vez completados los campos (o a medida que los va rellenando, sobre la marcha) puede ir probando lo que se ejecuta. Si encuentra problemas para resolverlo pulse el botón azul, encontrará un grafcet explicativo y a continuación la solución del problema.
Reglas que afectan a los saltos de etapas:
Pulse el botón azul del programa anterior para ver el grafcet explicativo, donde se ven las lineas de salto y tómelo como referencia. Las reglas pueden considerarse las mismas que en una cadena lineal y su aplicación es muy sencilla:
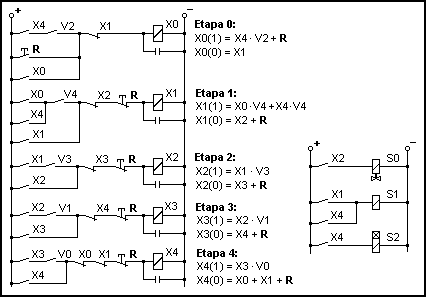
1.- Cada etapa se conecta con la anterior y la transición que le sigue. Para aplicarlo a la conexión de la etapa 1 hay que tener en cuenta que la etapa anterior puede ser la 0 o puede ser la 4, luego será X1(1) = X0 · V4 + X4 · V4 = ( X0 + X4 ) · V4.
1.- Cada etapa se desconecta con la etapa siguiente. Para aplicarlo a la desconexión de la etapa 4 hay que tener en cuenta que la etapa siguiente puede ser la 0 o puede ser la 1, luego será X4(0) = X0 + X1 + R (añadiendo una condición de reset R para conectar la primera etapa y desconectar todas las demás, incluída la 4).
El siguiente cuadro representa la aplicación de estas reglas para obtener un esquema de contactos:

Aunque el caso resuelto corresponde a repetición de etapas, no deja de ser un salto hacia algún punto concreto de la cadena secuencial, no importa si el salto es atrás o adelante, las reglas son las mismas cuando se localiza la etapa o etapas anteriores y siguientes. Se resuelven igualmente los casos de selección de secuencia, es decir, cuando son posibles dos caminos diferentes a partir de una etapa determinada (la etapa en la que se juntan los caminos tendrá dos etapas anteriores).