 figura 1
figura 1
Como se ha dicho, muchos procesos industriales tienen una característica común: Que son autorregulables. Si tenemos que hacer alguna intervención y sabemos que el proceso es autorregulable, la teoría que se describe en este apartado se podrá saltar, porque en el siguiente se hará una recopilación de lo que es importante en este tipo de procesos, sin detenernos en las justificaciones teóricas.
Cada elemento o parte de un proceso convierte una determinada magnitud física en otra magnitud, que puede ser de distinta naturaleza. Por ejemplo, un sensor de nivel nos informa sobre el nivel de líquido en un depósito mediante una señal eléctrica de tensión proporcinal al nivel que mide. Según la figura 1, una magnitud X se convierte en otra magnitud Y según una relación lineal (una recta que pasa por el origen). El factor K por el que hay que multiplicar a la magnitud X para obtener la respuesta Y se denomina ganancia. Cada elemento se puede representar por un bloque que recibe una magnitud de entrada (X) y devuelve como respuesta otra magnitud (Y). El valor de la respuesta Y no se alcanza necesariamente de forma instantantánea cuando hay una variación en el valor de entrada X. En el ejemplo de la figura 1 vemos que al variar la entrada bruscamente de 0 a 1, la salida alcanza el valor final progresivamente a medida que pasa el tiempo. Esta representación (en función del tiempo) no es una recta, pero esto no significa que el comportamiento no sea lineal. Un comportamiento es lineal cuando el valor final de la salida es proporcional a la entrada, no al tiempo que se necesita para alcanzar dicho valor final. La respuesta de un elemento o parte de un proceso se analiza considerando como entrada un valor que pasa bruscamente de 0 a 1, que se conoce como escalón unitario.
 figura 1
figura 1La mayoría de los reguladores industriales son lineales, a pesar de que los procesos siempre tienen partes con un comportamiento no lineal. En la figura 2 vemos un ejemplo de comportamiento no lineal y cómo se puede aproximar a lineal: En cualquier proceso, los márgenes de variación de las magnitudes tienen unos límites, de modo que siempre se puede definir un punto central de funcionamiento, en cuyas proximidades se podrá aceptar como lineal cometiendo un error aceptable. Según este principio, el análisis del proceso y el ajuste del regulador deberá hacerse en las proximidades del punto de funcionamiento. Esto garantizará que la regulación será buena siempre y cuando el proceso no se desvíe demasiado del punto de funcionamiento, en caso contrario no podemos predecir la respuesta, siendo posible, incluso, que se vuelva inestable (fuera de control).
 figura 2
figura 2Para corregir el comportamiento de un proceso es necesario medir y así conocer el error cometido para poder corregirlo. Una regulación que funciona de esta forma es una regulación en lazo cerrado. La precisión de la medida es fundamental, de forma que un sensor no lineal es inaceptable, sin embargo, algunos sensores no lineales tienen otras buenas características que compensan su falta de linealidad, después de todo la no linealidad se puede corregir con algún sistema electrónico (acondicionador de señal, generador de funciones...) o en el propio programa de control (solo en caso de ser programado, no existiendo regulador físico). En cualquiera de los dos casos, la solución pasa por una equivalencia entre la señal recibida y la que se debe considerar. La tendencia más generalizada es que el sensor incluya la electrónica necesaria para linealizar su respuesta y este conjunto de elementos (sensor y acondicionador) recibe el nombre de transductor. En la figura 3, la tabla en el interior del segundo bloque convierte un valor (Y) no lineal en otro valor (Z) igual al valor de entrada (X). El conjunto de los dos bloques será un bloque lineal con ganancia igual a 1.
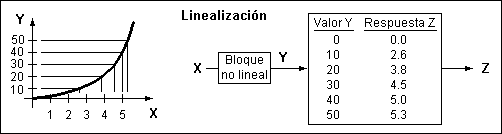 figura 3
figura 3Según todo lo anterior, los procesos pueden ser lineales o no lineales. Los no lineales son muy complejos y en la mayoría de los casos se controlan con reguladores lineales, buscando una buena respuesta en las proximidades de un punto central de funcionamiento y aceptando errores más importantes a medida que el sistema se aleje de dicho punto.
1.- ¿Cuáles de los siguientes comportamientos se pueden considerar lineales?:
| a) Presión en el fondo de un líquido (entrada) y nivel del líquido (salida). |
| b) Diferencia de presiones a ambos lados de una válvula (entrada) y el caudal que circula (salida). |
| c) La señal que llega a un amplificador (entrada) y la señal que transmite (salida). |
| d) La velocidad de rotación en el eje de una dinamo (entrada) y la señal eléctrica que transmite (salida). |
Por suerte, todo proceso lineal se compone de partes que se comportan según unos pocos patrones de respuesta y permiten representarlo gráficamente por medio de unos bloques característicos. Cada bloque tiene una entrada y una salida. Normalmente, la respuesta del bloque se considera para una entrada que pasa bruscamente de valor 0 a valor 1 y que se conoce como "escalón unitario". Dentro del bloque, se dibuja cómo es su respuesta para ese escalón unitario. En la figura 4 se encuentran los diversos tipos de bloques en que se puede descomponer un proceso:
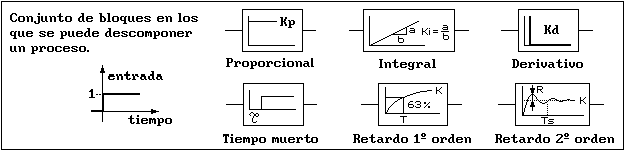 figura 4
figura 4Cuando la respuesta de un determinado elemento o sistema es proporcional a la magnitud de entrada que recibe, puede tratarse como un bloque proporcional. Un ejemplo lo podemos encontrar en la simulación de nivel: El sensor o elemento de medida, incluyendo todos sus componentes, tiene como magnitud de entrada el nivel de líquido y su salida es una señal eléctrica cuya tensión es proporcional al nivel. La constante de proporcionalidad (Kp según figura 4) se conoce como "ganancia" y es igual al cociente de la variación en la salida y la variación en la entrada. Dicho de otra forma, la salida es igual a la entrada multiplicada por la ganancia. Los demás tipos de bloques también tienen una ganancia (y otros parámetros adicionales). El dibujo de un bloque proporcional es una linea horizontal porque ya se dijo que se considera una entrada tipo escalón y como la respuesta es proporcional, será igualmente un escalón (más alto si Kp es mayor que 1 y más bajo si Kp es menor que 1). Otro claro ejemplo es un amplificador, cuya función es precisamente amplificar la entrada de forma proporcional. Como ejemplo mecánico tenemos la palanca, en la que al aplicar una fuerza en un extremo se consigue otra fuerza en el otro extremo que es proporcional a la aplicada.
2. ¿Cuáles de los siguientes casos se pueden tratar como un bloque proporcional?:
| a) Fuerza aplicada a un resorte (entrada) y alargamiento del resorte (salida o respuesta). |
| b) Fuerza aplicada a un amortiguador (entrada) y velocidad resultante (salida). |
| c) Presión aplicada en un pistón (entrada) y la fuerza que desarrolla (salida). |
| d) Corriente que entra en un condensador (entrada) y la tensión que alcanza (salida). |
| e) Tensión entre extremos de una resistencia (entrada) y la corriente que circula (salida). |
| f) Desplazamiento en un potenciómetro lineal (entrada) y tensión que transmite (salida). |
| g) Caudal de entrada en un depósito cerrado y nivel que alcanza (salida). |
Cuando un elemento o sistema acumula la magnitud de entrada se comporta como un bloque integral (o integrador). En la simulación de nivel encontramos un caso: Considerando como entrada el caudal que llega al depósito y como salida el nivel que alcanza, es claro que para un caudal constante se irá acumulando líquido y el nivel irá creciendo. Lógicamente la válvula de vaciado, que es parte del sistema, modifica este comportamiento, pero esto ya se verá cuando se represente la descomposición en bloques de todo el sistema. Otro ejemplo puede ser considerar como entrada la velocidad de un movil y como salida el espacio que recorre, ya que para una velocidad constante, el espacio crece contínuamente. Considerando como entrada un escalón (valor constante), es claro que el integrador mantiene a la salida creciendo indefinidamente, de ahí la recta ascendente de su símbolo. La ganancia de un integrador es infinito porque el valor final de la salida sería teóricamente infinito, siempre que la entrada se mantenga constante un tiempo infinito.
3. ¿En qué casos de la cuestión 2 se define un bloque integrador?:
4. En la figura 5, la señal verde se aplica como entrada en un integrador y este devuelve como salida la señal roja, ¿cuál de los siguientes casos es el correcto?
 figura 5
figura 5Cuando un elemento o sistema devuelve como salida la rapidez con la que varía la magnitud de entrada es un elemento derivativo. Un ejemplo puede ser el ángulo que gira el eje de una dinamo (como entrada) y la tensión eléctrica que aportará la dinamo (como salida). De hecho, una dinamo tacométrica se utiliza como sensor de velocidad en muchas ocasiones. No se olvide que una velocidad es la rapidez de variación de la posición y por lo tanto, cualquier elemento que informe sobre velocidad será un elemento derivativo. Otro ejemplo un poco más difícil de comprender es un condensador en serie, que al recibir una señal eléctrica en uno de los extremos, transmite por el otro extremo otra señal igual a la rapidez de variación de la primera. Esto hace posible que se elimine la componente continua de una señal alterna, siendo la salida igual a la entrada pero sin componente contínua y adelantada un cuarto de ciclo (90º). Velocidad, rapidez y derivada son conceptos equivalentes. Gráficamente, si se representa la variación de una posición y se traza una tangente a la curva en cualquier punto, la pendiente de la tangente coincidirá con la velocidad en ese instante y es igualmente la derivada de la función en el punto de tangencia o la rapidez con que varía la posición en ese instante. En la simulación, la única parte derivativa es una de las acciones del regulador, que de momento estará anulada. La gráfica del bloque derivativo es un trazo vertical porque la señal de entrada, que sufre una variación brusca (un escalón), tiene una rapidez de crecimiento infinito (la pendiente de una vertical es infinito) y justo después se hace constante por lo que ya no crece y la salida se hace cero. Cuando un elemento derivativo recibe un salto brusco (como un escalón), el valor de la salida será un pico de tensión tan elevado como permita el elemento derivativo, pero se anula inmediatamente porque se considera entrada constante. La ganancia de un elemento derivativo es 0 porque la rapidez de crecimiento de una entrada constante es cero.
5. Aplicando en un borne de un condensador una señal como la gráfica verde (figura 6), se obtiene en el otro borne otra señal que se dibuja en rojo, ¿cuál de los siguientes casos es el correcto?
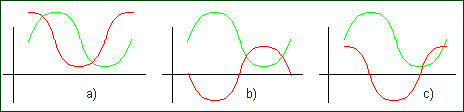 figura 6
figura 6Un elemento o sistema que devuelve la misma magnitud de entrada pero con un cierto retraso, será un retardo puro o tiempo muerto. En la práctica no se utilizan elementos con este tipo de comportamiento porque los tiempos muertos son la principal causa de inestabilidad. Sin embargo, todos los elementos reales tienen en mayor o menor grado un tiempo muerto, por ejemplo, un movil en reposo no se pone de forma instantánea en movimiento debido a su inercia, un sensor de temperatura no percibe inmediatamente la variación de temperatura porque pasa un tiempo desde que el calor sale del foco de emisión hasta que llega al sensor y lo hace reaccionar. En la regulación de nivel, el tiempo muerto más significativo puede estar en la tubería, pues la masa de líquido tiene una inercia que cuesta vencer, así, cuando hay un aumento en las revoluciones de la bomba, el rotor bate el líquido sin que aumente su circulación, hasta que se va venciendo su inercia. La ganancia de un tiempo muerto es 1, es decir, la salida alcanza exactamente el mismo valor de entrada.
6.- De los siguientes casos, ¿en cuál se puede esperar el mayor tiempo muerto?
| a) En el conjunto variador-motor-bomba del sistema de nivel. |
| b) En el movimiento de un movil con masa reducida. |
| c) En un sensor de temperatura. |
Un elemento o sistema se comporta como un retardador simple o de primer orden cuando la salida alcanza el valor de la entrada después de un cierto tiempo, pero no de forma instantánea sino que tiende a seguir a la entrada desde el primer instante. Generalmente aplica una ganancia K determinada, es decir, la salida termina alcanzando el valor de entrada multiplicado por esa constante K. El tiempo que tarda en alcanzar el 63% del valor final se denomina constante de tiempo T y alcanza prácticamente el valor final (95%) en un tiempo 3T. Como ejemplos puede citarse el caudal de salida de un depósito, que va creciendo cada vez más despacio hasta igualarse con el caudal de entrada. También la velocidad de un motor de corriente continua de imanes permanentes respecto de la tensión de entrada en el inducido, o la tensión de salida de un circuito RC (entre extremos del condensador) respecto de la tensión de alimentación. En general, ocurre con la mayoría de los sistemas con una inercia que se opone a las señales de entrada.
7.- ¿Cuáles de los siguientes casos se pueden tratar como un retardo de primer orden?
| a) Tensión aplicada a una resistencia y condensador en serie (entrada) y tensión entre extremos del condensador (salida). |
| b) Flujo de calor de una fuente calorífica (entrada) y temperatura que alcanza la sala (salida). |
| c) Fuerza aplicada a un amortiguador (entrada) y velocidad que resulta (salida). |
| d) El peso de un objeto (entrada) y su velocidad en caída libre (salida). |
| e) Altura máxima de elevación en una bomba centrífuga (entrada) y altura real alcanzada (salida). |
Un elemento o sistema se comporta como un retardo de segundo orden si almacena energía y la devuelve con retraso, produciendo una oscilación. Los parámetros que caracterizan este comportamiento son (figura 4): R es el rebasamiento máximo, K es la ganancia del elemento, Ts es el tiempo necesario para alcanzar un régimen de equilibrio, entendiendo como tal el tiempo a partir del cual el error está dentro de una tolerancia de +2 y -2% del valor final. Un ejemplo de sistema retardador de segundo orden es el conjunto masa-muelle-amortiguador: El muelle acumula la energía cinética de la masa y la devuelve con retraso; el amortiguador origina la disminución de la oscilación por el rozamiento fluido. Otro ejemplo es el circuito RLC (resistencia-bobina-condensador), que produce una tensión entre los extremos del condensador de una forma oscilante y amortiguada cuando se aplica bruscamente una tensión de alimentación. Un sistema con este comportamiento tiene una frecuencia natural de oscilación y cuando se les aplica una energía pulsatoria de igual frecuencia, es posible que la oscilación aumente hasta que el sistema se destruya. Este fenómeno se conoce como resonancia y puede ser muy perjudicial, aunque a veces se aplica para conseguir oscilaciones mantenidas (osciladores). En los circuitos con bobinas, se puede alcanzar una tensión muy superior a la de alimentación y resultar especialmente peligrosos, incluso con la alimentación desconectada. Por esta razón, en el diseño de estos circuitos se debe haber previsto el fenómeno de resonancia. En la simulación de nivel, no existen elementos con este comportamiento, pero cuando se utilice el regulador veremos que todo el sistema en conjunto sí puede tener este comportamiento como resultado de un ajuste inadecuado, hasta el punto de responder como un oscilador.
8.- ¿Cuáles de las siguientes afirmaciones son ciertas?
| a) En un circuito RLC y masa-muelle-amortiguador son equiparables resistencia-amortiguador, bobina-muelle y condensador-masa. |
| b) En un circuito RLC y masa-muelle-amortiguador son equiparables resistencia-masa, bobina-amortiguador y condensador-muelle. |
| c) En un circuito LC (sin resistencia), al aplicar un impulso de tensión, la tensión en el condensador es pulsatoria y muy poco amortiguada. |
| d) Por un camino ondulado o con baches, la oscilación de un vehículo depende de su velocidad. |
La relación que guardan los bloques en que se divide un sistema puede ser de tres tipos (figura 7). Dos bloques están en paralelo cuando sus respuestas se suman. Por ejemplo, un comportamiento cuya gráfica es una recta ascendente que pasa por encima del origen, es el resultado de sumar los efectos de un bloque proporcional y un integrador. Dos bloques están en cascada cuando sus respuestas se superponen, es decir, cuando la respuesta de uno de ellos es afectada de acuerdo con la respuesta del segundo. Por ejemplo, un retardo de segundo orden cuya gráfica no comienza en el instante cero sino más tarde, es equivalente a un retardo de segundo orden y un tiempo muerto conectados en cascada. Dos bloques están en realimentación cuando la salida de uno de los bloques se realimenta (vuelve atrás) para influir en su entrada. El comportamiento de esta realimentación está marcado por el otro bloque. En la figura 7, la salida del bloque 1, modificada según la ley que imponga el bloque 2, se resta a la entrada. La realimentación es el principio básico para poder regular, ya que implica una medida de la respuesta y una corrección de la entrada para disminuir el error.
 figura 7
figura 7Aplicación al sistema de nivel.
En la circulación de un líquido por una tubería, solo se establece una circulación entre dos puntos cuando existe una diferencia de presiones entre dichos puntos. Ya que la presión en el fondo y la altura son términos proporcionales, se puede decir que se establece una circulación cuando existe una diferencia de niveles. Esto se pone de manifiesto entre dos recipientes comunicados, entre los que hay una circulación hasta que los niveles se igualan. Al funcionar una bomba centrífuga se alcanza una altura máxima de elevación (Hmax según figura 8) que se podría medir si se dispone de un tubo como se representa en la figura. El caudal que entrará al depósito dependerá de la diferencia de nivel (Hmax - Hreal), como si se tratara de una circulación entre dos recipientes. En estas condiciones, el caudal irá disminuyendo hasta que el nivel real (Hreal) alcance al máximo, momento en el que el caudal será cero. Si disminuye el número de revoluciones, Hmax también disminuye, pudiendo ser inferior al nivel real. Si esto sucede, la circulación puede cambiar de sentido, vaciándose el depósito a través de la bomba hasta que los niveles máximo y real se igualen de nuevo. Si las revoluciones siguen disminuyendo, Hmax puede hacerse inferior a Hmin (altura de la bomba), en cuyo caso el nivel real también bajará, entrará aire en la bomba y hará imposible seguir bombeando posteriormente. Para evitar este inconveniente se coloca un antirretorno, de forma que una vez cebada la bomba ya no sea posible la entrada de aire y la circulación solo puede ser ascendente. Esto significa que existirá un número de revoluciones por debajo del cual no será válida ninguna medición sobre el proceso. Así pues, será necesario determinar la señal de mando mínima, que aplicada al variador, haga llegar la altura máxima de elevación hasta el depósito (Hdep). Otra consideración importante es que la altura de la bomba no debe ser mayor de un valor determinado, que depende del fluido a bombear, pero esto también depende de la sección de la tubería de aspiración: Cuanta menor sección y cuanta mayor altura, más fácil será que el líquido entre en ebullición y la bomba trabajará en vacío sin capacidad para bombear el líquido. Tratándose de agua, la altura máxima de aspiración (Hmin en la figura 8) es de 10.33 metros pero en la práctica no se consigue aspirar por encima de unos 6 metros.
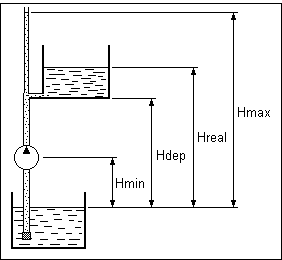 figura 8
figura 89.- Para determinar datos del sistema, la altura máxima de elevación:
| a) Debe ser mayor que la altura de la bomba. |
| b) Debe ser mayor que la altura de la base del depósito. |
| c) Debe ser mayor que la altura real. |
| d) Todas son correctas. |
| e) Todas son falsas. |
La descomposición en bloques del sistema de nivel puede ser la que aparece en la figura 9. El variador es un bloque proporcional porque se trata básicamente de un amplificador de tensión (si el motor es de corriente continua) o de un variador de frecuencia que aporta una frecuencia proporcional a la señal de entrada. El motor, que se alimenta del variador, alcanzará un número de revoluciones que será proporcional a la señal de entrada (tensión o frecuencia), aunque no instantáneamente, por lo que debería considerarse un retardo de primer orden. Pero el retardo será muy pequeño comparadado con otros retardos del proceso como el debido a la inercia del líquido, luego podremos aceptar que será un bloque proporcional. La bomba, que convierte revoluciones en altura máxima de elevación, tiene un comportamiento no lineal. Esto se debe a que la energía cinética depende del cuadrado del número de revoluciones (la velocidad) y como esta energía se transforma en energía de presión, resultará una presión (o altura máxima) que también depende del cuadrado de la velocidad. Para aceptar a la bomba como lineal, será necesario considerar como punto de funcionamiento el correspondiente al nivel central en el depósito, que parece lo más razonable, aceptando una regulación menos buena cuando el depósito esté casi lleno o casi vacío. De esta forma, el comportamiento de la bomba se podrá considerar proporcional (no es de esperar retardo en alcanzar la altura de elevación cuando varía el número de revoluciones).
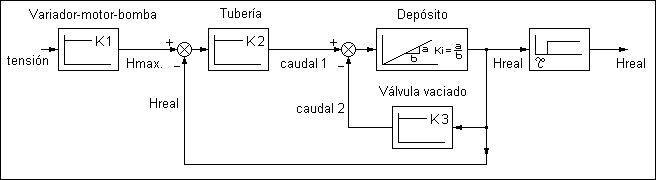 figura 9
figura 9Como ya se ha explicado, el caudal que circula por la tubería dependerá de la diferencia de niveles (Hmax - Hreal), de ahí el punto de resta que determina la primera realimentación. El caudal que llega al depósito (caudal 1) no es proporcional a la diferencia de nivel sino a su raíz cuadrada (se necesitan incrementos de nivel cada vez mayores para conseguir incrementos iguales de caudal). La tubería tiene un comportamiento no lineal que exige, como sucede con la bomba, definir un punto central de funcionamiento. Así aceptamos como más aproximado, un comportamiento proporcional. Un caudal constante que entra en un depósito hace que el nivel aumente linealmente con el paso del tiempo (es un integrador), pero existe una válvula de vaciado y con ella un caudal de salida que se resta al de entrada, resultando el segundo nudo de resta que determina una nueva realimentación. Como sucedía con la tubería, el caudal que pasa por la válvula de vaciado es proporcional a la raíz cuadrada del nivel (en este caso el nivel en el depósito) y por la misma razón la consideramos como bloque proporcional. Finalmente, para tener en cuenta los tiempos muertos de todo el sistema (cuya estimación elemento por elemento es muy compleja), ha sido añadido un tiempo muerto al final del diagrama.
El diagrama de bloques debe simplificarse hasta convertirlo en un solo bloque final, que nos informará acerca de los parámetros del sistema que lo caracterizan. Matemáticamente, cada uno de los 6 tipos de bloque tiene una función equivalente llamada función de transferencia y siempre es posible la simplificación y el estudio de la estabilidad. Es el procedimiento que mejores resultados aporta pero debido a su complejidad nos conformaremos con una simplificación intuitiva y gráfica (figura 10).
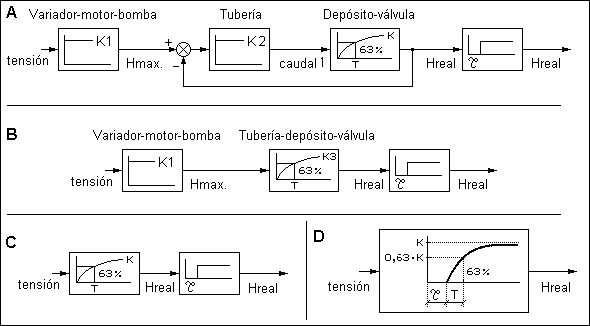 figura 10
figura 10Los bloques en realimentación son los más dificiles de interpretar, pero hay casos más sencillos como sucede con el conjunto depósito-válvula de vaciado: A medida que aumenta el nivel real (figura 9), el caudal de salida de la válvula también aumenta. Como este caudal se resta al de entrada, el caudal resultante irá disminuyendo hasta hacerse 0 y desde ese momento se mantendrá constante el nivel. Como el caudal resultante disminuye, el nivel irá creciendo cada vez más lentamente, lo que corresponde a un retardo de primer orden (simplificación A de la figura 10). La realimentación de alturas es un poco más complicada: Al aumentar la altura real, la diferencia disminuye, haciendo que se retarde más el crecimiento, pero la altura real no puede alcanzar a la máxima si está abierta la válvula de vaciado, de modo que la diferencia no llega a hacerse cero y se mantiene una altura real mayor de cero. El resultado sigue siendo el mismo que si se elimina la realimentación, modificándose solamente los valores de las ganancias y la constante de tiempo. Un bloque proporcional solo se define por una ganancia pero no altera el comportamiento, así, en la simplificación B de la figura 10 (eliminada la realimentación) resulta un retardo de primer orden con una ganancia K3 igual al producto de las ganancias (K2 · K). Los dos primeros bloques (en la simplificación B) vuelven a corresponder a otro retardo de primer orden con una ganancia K igual al producto de las ganancias (K1 · K3), tal como aparece en la simplificación C de la figura 10. Por último, el tiempo muerto solo retarda un tiempo (Tau) al retardo de primer orden (simplificación D).
Hasta el momento no se ha tenido en cuenta la señal del sensor ni el regulador, es decir, se trata de una regulación en lazo abierto porque no se ha considerado la medida del nivel (para calcular el error y corregirlo). Como se deduce de la última simplificación, el proceso de regulación de nivel se define por tres parámetros: Una ganancia K, una constante de tiempo T y un retardo puro (Tau). Los procesos con este comportamiento tan característico se conocen como sistemas autorregulables. Estos procesos se pueden hacer funcionar en lazo abierto sin perder la estabilidad, ya que garantizan que para una señal de entrada constante se alcanza un equilibrio de la magnitud controlada, que se alcanza progresivamente y tiene un límite.
En el siguiente apartado (Determinación de los parámetros) se describe cómo determinar los parámetros del proceso y los parámetros de ajuste del regurador para controlar el proceso en lazo cerrado, es decir, midiendo el nivel, calculando el error y corrigiéndolo de la forma más exacta y rápida posible.
10.- La regulación de nivel:
| a) Es autorregulable pero existen límites físicos fuera de los cuales no hay regulación. |
| b) Es igual de precisa para cualquier nivel a controlar. |
| c) Nunca puede hacerse en lazo abierto porque es inestable. |
| d) Es óptima solamente si el nivel se mantiene próximo a un valor fijo. |
| e) Solo puede ser controlado con un regulador no lineal. |
SOLUCIONES:
1.- El nivel de un líquido sí es proporcional a la presión en el fondo, tanto es así que frecuentemente expresamos presiones en términos de alturas, como por ejemplo de columna de agua o milímetros de columna de mercurio (correcto a). El caudal es proporcional a la raíz cuadrada de la diferencia de presiones, no a la diferencia, que es la entrada, luego el caso b es falso. Un amplificador está diseñado expresamente para transmitir una señal proporcional a la entrada (correcto c). La corriente eléctrica inducida es proporcional a la rapidez de variación del flujo magnético, que a su vez es proporcional a la velocidad (correcto d).
2.- Correcto a. Falso b porque en un amortiguador hay rozamiento con un fluído y con fuerza constante, la velocidad crece de forma cada vez más lenta hasta que se hace constante. Correcto c. Falso d porque una corriente constante de entrada supone una acumulación de carga eléctrica y un progresivo aumento de tensión. Correcto e siempre y cuando no se conecte otra carga en paralelo con la recistencia. Correcto f siempre y cuando la señal que transmite se aplique a un dispositivo de impedancia muy elevada, ya que en caso contrario sucede lo mismo que al conectar una carga en paralelo con la resistencia del caso e. En la simulación, la entrada de consigna del regulador y la entrada de control en el variador, se comportan prácticamente como un aislante y no suponen carga apreciable para los potenciómetros. Falso g porque un caudal de entrada constante implica una acumulación de fluido y por lo tanto el nivel crece.
3.- Son integradores los casos d y g.
4.- Un integrador acumula la señal de entrada. Gráficamente, esto significa que se puede calcular la salida como el área entre la gráfica verde y el eje horizontal, siendo positivo si está por encima del eje y negativo si está por debajo. Según esta aclaración, el área va creciendo hasta que la linea verde corta al eje (punto central) y luego va disminuyendo porque se irá restando área por estar la linea verde por debajo del eje. Los casos a y b cumplen lo descrito, pero es correcto el b porque el área que se resta comienza siendo muy pequeño desde el punto central y la respuesta decrece lentamente al principio.
5.- Un condensador en serie es un elemento derivativo. En la cresta y valle de la señal verde (entrada) la rapidez de crecimiento es cero (horizontal), luego la derivada tiene que ser cero en esos puntos. El único caso que lo cumple es el c.
6.- En un sensor de temperatura, el tiempo muerto es verdaderamente importante, ya que para que el sensor detecte una variación, es necesario que el calor se transmita a través de un medio, lo que sucede a baja velocidad (correcto c).
7.- Al aplicar tensión al conjunto resistencia-condensador, el condensador se va cargando y aumentando la tensión entre sus extremos. Pero la carga tiene un límite, que una vez alcanzado deja de haber corriente eléctrica y la tensión se mantiene constante (correcto a). A medida que aumenta la temperatura, el flujo de calor que se pierde también aumenta. Cuando este flujo se iguala al que produce la fuente de calor, el flujo resultante se hace cero y la temperatura se mantiene (correcto b). En un amortiguador existe una fuerza de rozamiento fluido que es proporcional a la velocidad. A medida que la velocidad crece, también crece la fuerza de rozamiento y acaba igualándose con la fuerza aplicada. Desde ese momento, la fuerza resultante es cero y la velocidad se mantiene constante (correcto c). En la caída libre de un objeto existe un rozamiento fluido con el aire de modo que se comporta igual que el caso anterior (correcto d). Al aumentar las revoluciones de una bomba, el salto de presión que aplica la bomba es proporcional a la variación de revoluciones. Para la presión resultante, la altura máxima que puede alcanzar el líquido es proporcional a la presión. De hecho, en los saltos de agua es típico indicar presiones como alturas. Por lo tanto, si las revoluciones son constantes (un escalón), también lo será la altura máxima. A medida que el nivel se aproxima a la altura máxima, es lógico que el caudal tiene que ir disminuyendo hasta que finalmente se hace cero. Un caudal que disminuye, significa que el nivel crece cada vez más despacio, hasta que se hace constante a la altura máxima (correcto e).
8.- La resistencia equivale al amortiguador porque ambos limitan la transferencia de energía. La bobina equivale al muelle porque almacena energía (electromágnética) que devuelve con retraso. El condensador equivale a la masa porque ambos mantienen la energía en el sistema, el condensador como campo eléctrico y la masa como energía cinética (correcto a). En un circuito LC solo existe la resistencia de una bobina y de un condensador, que es muy baja, por lo tanto la amortiguación es mínima (correcto c). La frecuencia con la que las ondulaciones o baches afectan al vehículo depende claramente de su velocidad. Como la suspensión de un vehículo es un conjunto masa-muelle-amortiguador, es claro que existirá una velocidad para la que las ondulaciones o baches llegarán con una frecuencia igual a la de oscilación del sistema. Cuando esto sucede, las oscilaciones pueden aumentar y causar problemas (correcto d).
9.- Si la altura máxima no alcanza a la base del depósito no habrá caudal de entrada al depósito, pero sí podrá haber caudal de salida. Puesto que el nivel se equilibra cuando los dos caudales se igualan, es necesario un caudal de entrada para encontrar el equilibrio (correcto b).
10.- Es autorregulable pero efectivamente hay límites que pueden causar el desbordamiento o la falta de caudal de entrada (correcto a). Es un proceso no lineal, por lo que solo es óptima en las proximidades de un punto de funcionamiento (un nivel fijo) pero no para cualquier nivel. No es inestable, ya que en un proceso autorregulable se estabiliza fácilmente la magnitud a controlar. Es óptima solo en las proximidades de un punto de funcionamiento (correcto d). Aunque no es lineal, en la práctica se controla casi todo con reguladores lineales, por la dificultad que entraña analizar el proceso como no lineal.