figura 1
Comenzaremos por determinar qué señal de mando (aplicada al variador) se necesita como mínimo para que la altura de elevación de la bomba alcance el depósito. Esto podrá hacerse aumentando poco a poco la señal de mando y vigilando el nivel. Comenzaremos con la válvula de vaciado completamente abierta (manecilla vertical), depósito vacío y control manual (llega al variador la señal del segundo potenciómetro). Ponga el selector en la posición derecha para ver la señal del sensor (realimentación) y desplace poco a poco el cursor del potenciómetro de control manual hacia la izquierda. Se comprueba que no aparece líquido en el depósito hasta poco antes de que el cursor llegue al valor 4. Por lo tanto, aceptaremos que las posteriores comprobaciones solo serán fiables con señales de mando del variador mayores o iguales a 4 voltios. Por encima de 4 voltios, el control es válido hasta el límite de 10 voltios, ya que se comprueba que el nivel es afectado por cualquier cambio de la señal de mando si está entre 4 y 10 voltios.
1.- ¿Porqué se ha dejado la válvula de vaciado completamente abierta para comprobar el margen de funcionamento admisible?
| a) La apertura de la válvula no tiene importancia, puede servir cualquiera. |
| b) Se ha dejado abierta para evitar que el depósito se llene y se desborde por descuido. |
| c) Se ha dejado abierta porque se trata de encontrar las condiciones más desfavorables (el margen más reducido). |
2.- Si las revoluciones varían entre 0 y 3000 rpm cuando la señal de mando varía entre 0 y 10 voltios, ¿cuál es la velocidad mínima que garantizará
un control dentro de límites admisibles?:
| a) 500 rpm b) 1200 rpm c) 2300 rpm |
3.- Suponiendo que el sistema se ha diseñado correctamente (antes funcionaba bien), si en el experimento anterior la bomba no subiera líquido para
ninguna velocidad, el problema se debería a:
| a) Altura total de elevación excesiva. |
| b) Altura de aspiración excesiva. |
| c) La bomba ha aspirado aire. |
| d) El antirretorno no cierra correctamente. |
| e) La rejilla de aspiración está obstruída. |
Suba bruscamente la señal de mando manual hasta 8 voltios, por ejemplo. Verá que el nivel sube deprisa al principio pero disminuye progresivamente la velocidad hasta que después de un tiempo se estabiliza en 6.514 voltios (puede cambiar el selector cuando quiera para ver la señal de mando manual o la de realimentación). Para conseguir un cambio brusco hasta los 8 voltios bastará con pulsar justo debajo del valor 8 en el potenciómetro y el cursor cambiará inmediatamente. Esta es una forma de conseguir señales de tipo "escalón", que como veremos, son muy empleadas para tomar datos del proceso.
4.- ¿A qué se debe que el nivel se estabilice con señal de mando manual invariable?:
| a) A que el variador reduce la velocidad de la bomba a medida que sube el nivel. |
| b) A que se alcanza la altura máxima de elevación de la bomba. |
| c) A que los caudales de entrada y salida se igualan. |
Una regulación que no tiene en cuenta la señal de realimentación se dice que es en "lazo abierto" (el control manual que acaba de experimentar lo ha hecho de esta manera). Si en el control se tiene en cuenta la realimentación (señal del sensor) se dice que es en "lazo cerrado". Para cerrar el lazo en la simulación bastará con cambiar de estado el conmutador "A", ya que entonces actúa el regulador, que tiene en cuenta la realimentación para calcular la señal de salida (control). Los procesos que se estabilizan en lazo abierto se denominan "procesos autorregulables". Un control de nivel es autorregulable porque el nivel llega a un equilibrio en lazo abierto, tal como ha comprobado si ha seguido las indicaciones. Esto no significa que el sistema se equilibra en todas las circunstancias, ya que todo tiene unos márgenes admisibles. Por ejemplo, si prueba con una señal manual de 10 voltios verá que el nivel sube hasta desbordar el depósito, incluso con la válvula de vaciado totalmente abierta. Pruebe a pulsar la tecla "A" para que el regulador actúe sobre el variador, con ello funcionará el proceso en lazo cerrado.
5.- Al abrir o cerrar el lazo de regulación, las consecuencias pueden ser:
| a) ¡Siempre una catástrofe! ya que los sistemas se diseñan para funcionar de una sola de las formas. |
| b) Si no se verifica que es posible el paso entre ambos modos y se pasa, se causarán perjuicios (dependiendo de la función del sistema). |
| c) Si no se vigila el proceso se pueden causar perjuicios, pero andando con vista no hay problema. |
No habrá ocurrido nada grave al pasar a lazo cerrado, pues solo se trata de una simulación, pero la realidad puede ser bien distinta. Para verificar si es posible el paso entre los dos modos de funcionamiento está la posición izquierda del selector de tres posiciones. En esta posición, el voltímetro marca la diferencia entre la señal del potenciómetro manual y la señal de control que sale del regulador. Cuando esta diferencia sea cero (o próxima a cero) se podrá pasar con seguridad y en caso contrario habrá consecuencias... Pase de nuevo a modo manual y aquí no ha pasado nada.
6.- ¿Porqué no era recomendable cambiar el proceso a lazo cerrado?
| a) Porque el regulador no regulaba, que es lo que debería haber hecho. |
| b) Porque la salida de control del regulador era cero y además no está ajustado |
| c) Porque se debería haber vaciado primero el depósito y así habría 0 voltios con selector en posición izquierda |
Aunque en la simulación no aparece, normalmente, los sensores se acompañan de un acondicionador de señal que permite ajustar los márgenes de la señal que transmiten (realimentación), así como conseguir que su variación sea proporcional a la variación de la variable regulada (nivel en este caso). Este conjunto sensor-acondicionador recibe el nombre de "transductor". Los ajustes indicados son un "offset" y una "ganancia". El offset ajusta la señal del sensor (realimentación) para poder ponerlo a cero con un determinado valor de la variable regulada (nivel en este caso) y la ganancia es el factor de conversión de unidades, que se calcula como el cociente entre la variación de la señal del sensor y la variación de la variable gegulada, así por ejemplo, pudiera ser 0.1 voltios por cada centímetro de altura (nivel). Para ajustar los márgenes se procede de esta forma: Se manipula el proceso para que la variable regulada llegue al nivel en el que deseamos una señal igual a cero y ajustamos el offset hasta conseguir 0 voltios, luego se eleva la variable regulada hasta el nivel en el que deseamos una señal de 10 voltios (la máxima) y se ajusta la ganancia hasta conseguir los 10 voltios. Si se procede en orden inverso no es correcto, porque el offset altera la ganancia (el offset siempre debe ajustarse en primer lugar). Pruebe lo siguiente: Abra parcialmente la válvula de vaciado y ajuste el potenciómetro de control manual hasta conseguir 0 voltios de realimentación y luego haga lo mismo para 10 voltios de realimentación. Se comprueba que 0 voltios corresponden a depósito vacío, lo que significa que el offset había sido ajustado para tener una indicación igual a cero con el depósito vacío. También se comprueba que los 10 voltios corresponden a depósito completamente lleno (llega a desbordarse), lo que significa que había sido ajustada la ganancia para tener una indicación de 10 voltios con el depósito completamente lleno. Aunque la simulación no contempla un ajuste de offset y ganancia, no se debe creer que los sensores adaptan automáticamente su margen de medida a cualquier proceso.
7.- Si el depósito tiene una altura de 8 metros desde la base hasta la abertura superior, ¿cuál es la ganancia del sensor de nivel?:
| a) 1.25 volt./m b) 3 volt./m c) 0.8 volt./m d) 45 m/volt. |
En todo proceso existen "perturbaciones" que alteran el equilibrio. En general, son perturbaciones las variaciones de ganancia de los elementos cuya respuesta no es lineal. En una regulación de nivel, más concreto, la perturbación más característica es la apertura del orificio de vaciado. Si manipula la manecilla de la válvula podrá comprobar que el nivel se altera y si la deja en reposo se alcanza de nuevo el equilibrio (después de un tiempo) pero el nivel estable habrá cambiado, es decir, el nivel estable varía en función de la apertura de la válvula.
8.- Si se trata de mantener constante una variable regulada, se puede regular un proceso en lazo abierto en los siguientes casos:
| a) Cuando el proceso no sea autorregulable. |
| b) Cuando sea autorregulable y existan perturbaciones. |
| c) Cuando sea autorregulable y no existan perturbaciones. |
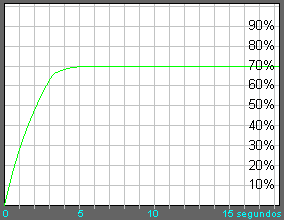
Industrialmente, el tiempo necesario para que una variable regulada alcance un valor de consigna determinado y se estabilice debe ser el menor posible, especialmente cuando se trata de un sistema de seguimiento, en el que no basta con alcanzar deprisa un valor constante, sino que se trata de alcanzar deprisa un valor variable (una consigna variable). Un ejemplo de sistema de seguimiento puede ser un eje en una máquina de control numérico. En este sistema, la consigna, que marca la posición a la que debe llegar la herramienta, es un valor que varía continuamente, de forma que combinado con los otros ejes define una trayectoria de la herramienta. En una máquina con 3 ejes, la tarea de seguimiento está triplicada y el esfuerzo de cálculo es muy importante. Se puede creer que un control de nivel tiene que ser mucho más sencillo que un control de posición, porque el posicionado se hace con velocidad muy superior. Esto es cierto solo parcialmente y para demostrarlo se propone la siguiente práctica: Deje la válvula de vaciado parcialmente abierta y ponga el selector en posición derecha para visualizar la señal del sensor. Luego manipule el potenciómetro de control manual para conseguir lo más rápidamente posible un nivel "estabilizado" del 70 % (7 voltios de realimentación). Vea que solo se pide conseguir un nivel constante, sin mencionar si quiera un seguimiento como sucede con la posición en máquinas. ¿Qué le parece? Me atrevería a decir que ¡fatal! Repita la experiencia, pero esta vez pulse la tecla "G" en el momento que decida comenzar el control. Desde ese momento se irá trazando una trayectoria de color verde que representa la señal del sensor (realimentación). Un buen control debería parecerse a la figura 1, que le servirá para comparar.
figura 1
9.- En toda regulación han de cumplirse unas especificaciones de funcionamiento. Trate de seleccionar cuáles son las más importantes:
| a) Mínimo tiempo de estabilización. |
| b) Realimentación oscilante. |
| c) Que la variable regulada alcance con rapidez a la señal de consigna. |
| d) Que la variable regulada sea estable (sin oscilaciones). |
| e) Que el actuador sea insensible a las perturbaciones. |
| f) Que la variable regulada se ajuste a la consigna con la mayor precisión posible. |
| g) Que la medida del sensor sea muy precisa y estable. |
Como conclusión, ya deberíamos tener claro que la regulación no es un problema tribial, porque cada proceso real tiene características que lo hacen muy complejo analíticamente. Un modelo matemático del proceso (y fiable) serviría para programar una ley de control óptima, pero en la práctica es verdaderamente difícil de conseguir (este tipo de añálisis se conoce con el nombre de respuesta temporal, osea, respuesta en función del tiempo). Un recurso alternativo es la determinación de datos del proceso, con los que se crea posteriormente el modelo matemático y se determina la estabilidad del sistema. Es más aplicable industrialmente porque solo se necesita un osciloscopio (y los componentes del proceso) y conocimientos matemáticos aceptables. Este análisis se conoce como respuesta en frecuencia y su fiabilidad es semejante a la respuesta temporal. En la actualidad existen reguladores muy sofisticados que pueden suplir a los dos procedimientos descritos, pero de momento, la sofisticación aún guarda una estrecha relación directa con la dificultad de uso y es por eso que los viejos reguladores PID siguen siendo los más ampliamente utilizados, por su facilidad de ajuste con unos resultados muy satisfactorios. Tenemos que ser conscientes de que la regulación depende en gran medida de las características del proceso concreto y por lo tanto es importante la experiencia que se tenga sobre el mismo. Por otra parte, la ley de control de un regulador nunca puede ser la solución óptima de control, sencillamente porque su respuesta solo depende del error (diferencia entre consigna y realimentación), sin conocer en absoluto cómo responderá el proceso, las desviaciones han de corregirse antes de que se manifiesten o de lo contrario será demasiado tarde y aparecerán oscilaciones. Cada regulador se caracteriza por determinados parámetros ajustables cuyos valores óptimos se pueden determinar por diversos procedimientos, que van desde la simple prueba y error hasta la sintonía analítica, pasando por otros procedimientos con dificultad creciente. En el ajuste de los parámetros tiene un papel importante la experiencia sobre el proceso que se deba regular. Sin ese conocimiento, el ajuste se convierte en un problema similar al de acertar la combinación de una caja fuerte.
10.- Un regulador debe satisfacer las siguientes exigencias para controlar óptimamente un proceso:
| a) Debe aportar una señal de control muy precisa y estable. |
| b) Debe programarse de acuerdo con el modelo matemático del proceso. |
| c) Debe aprender por su cuenta antes de conseguir un buen control. |
| d) Debe anticiparse a las desviaciones y corregirlas antes de que aparezcan. |
Para determinar los parámetros del proceso o cuando se hacen cambios y se desea comprobar el efecto, lo normal es disponer de un trazador porque aporta una ayuda insustituible. Suele tratarse de tarjetas electrónicas de adquisición de datos que se acoplan a un ordenador y se controlan por software. Con trazador, basta dejar funcioando al proceso y extraer luego la información de una gráfica. Sin trazador, habrá que vigilar la respuesta y medir tiempos con un cronómetro. A la hora de analizar el comportamiento en lazo cerrado, la gráfica permite extraer mucha información dificil de medir por otro procedimiento, como pueda ser la estabilidad, velocidad de respuesta, etc. La respuesta de un proceso autorregulable se puede ver en la figura 2.
figura 2Hay que indicar que la simulación de control de nivel responde a un modelo matemático teórico, presentando la práctica real alguna diferencia: Véase que en la figura 2, la gráfica no se eleva claramente desde el tiempo Tau, sino que lo hace con suavidad formando algo parecido a una S. Por este motivo, el tiempo Tau es impreciso y debe calcularse como se indica en la figura 2. Nótese que el valor Y1 de la respuesta no es cero, pues cabe esperar que exista un límite por debajo del cuál no existe regulación, esto ya se explicó en el análisis de la regulación de nivel. Lo mismo ocurre con la variación de la entrada (X2 - X1). Los tiempos T1 y T2 se pueden sacar de la gráfica si se dispone de un trazador o bien con cronómetro, anotando los tiempos cuando la respuesta alcanza el 28 % y el 63 % de su valor final. El problema es que el valor final no se conoce cuando la respuesta está creciendo y esto exige realizar dos veces la experiencia: La primera para obtener el valor final y la segunda para obtener los tiempos, pero asegurando que en la segunda varíe la entrada entre los mismos valores que en la primera y que todas las condiciones sean iguales, pues de lo contrario tendremos una respuesta con valores inicial y final diferentes. Como complicación añadida, los tiempos reales de estabilización pueden ser muy superiores a los de la simulación de nivel, haciendo que estas medidas sean delicadas y pesadas por los tiempos de espera.
Para deducir el comportamiento del sistema, vamos a tratarlo como un solo bloque con una entrada y una salida. La entrada se dará con el potenciómetro de control manual y la salida será la señal del sensor (realimentación). Como se ha deducido anteriormente, el valor de entrada no debe ser menor de 4 voltios. Para 4 voltios, la señal del sensor (realimentación) se estabiliza en 0.157 voltios. Puede comprobar esto ajustando 4 voltios con el potenciómetro de control manual y pasando luego el selector a la posición derecha para ver la señal del sensor.
Una vez estabilizado, habrá que aplicar un salto brusco en la entrada (un escalón), lo que se consigue pulsando en la guía del cursor del potenciómetro. Puesto que disponemos de un trazador de funciones, podemos ver cómo responde la señal del sensor. Para que la gráfica comience exactamente en el momento que se produce el salto, es necesario pulsar "a la vez" la tecla G y la guía del potenciómetro. La figura 3 muestra el resultado pulsando bajo el valor 8 de la escala del potenciómetro (a la vez que se pulsa la tecla G).
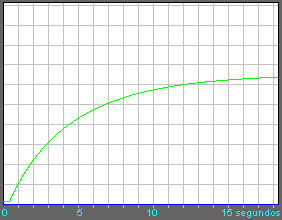figura 3De la gráfica extraemos toda la información para determinar los parámetros del proceso, sabiendo que la entrada ha sido un salto desde 4 hasta 8 voltios y la salida que devuelve el sensor (gráfica anterior) ha variado desde 0.157 hasta 6.514 voltios (dejando un tiempo suficiente hasta que la señal del sensor se estabiliza). Los parámetros del proceso son una ganancia K, una constante de tiempo T y un tiempo muerto Tau que se calculan según la figura 2.
11.- Según la gráfica de la figura 3, los parámetros de la regulación de nivel serán:
| a) K = 0.8125, T = 4.2 segundos y Tau = 0.3 segundos. |
| b) K = 3.95, T = 4.5 segundos y Tau = 2 segundos. |
| c) K = 1.589, T = 3.9 segundos y Tau = 0.4 segundos. |
El último paso consiste en determinar los parámetros del regulador y cerrar el lazo de regulación cambiando a modo automático (pulsando la tecla A). Un criterio experimental, que combina una rápida respuesta con un tiempo de estabilización aceptable es el criterio de amortiguamiento 1/4 (figura 4). Según este criterio, se garantiza que la segunda oscilación tendrá una amplitud igual a un cuarto de la amplitud de la primera oscilación.
figura 4La primera columna se aplicará si se desea únicamente la acción proporcional del regulador, anulando las acciones derivativa e integral. La segunda columna para acciones proporcional e integral (anulando acción derivativa). La tercera columna para las tres acciones. En cualquier caso, los parámetros del regulador se calculan a partir de los parámetros del proceso. Para anular alguna de las acciones, hay que introducir el valor 0 en el campo correspondiente, excepto en la acción integral, que se anula haciendo su parámetro Ti muy grande.
Podemos comenzar con acción proporcional solamente (regulador P), resultando Kp = T / (K · Tau) = 3.9 / (1.589 · 0.4) = 6.136. Introduzca este valor en el campo Kp del regulador, vacíe el depósito y pase luego a control automático con la tecla A. Seguidamente, pulse en el primer potenciómetro bajo el valor 6 (por ejemplo), a la vez que pulsa la tecla G para que se dibuje la respuesta. La gráfica resultante debería parecerse a la de la figura 5, donde se dibuja en rojo el salto en la señal de consigna, en azul la señal de control del regulador y en verde la señal del sensor (realimentación). Se comprueba que la medida o señal del sensor no alcanza a la consigna y la diferencia se denomina error estático. Se puede esperar que aumentando la acción proporcional disminuya el error, pero también disminuirá la estabilidad. Puede probar esto con un valor Kp igual a 20 (por ejemplo) y se verá que la respuesta es similar a la de un oscilador (sin amortiguamiento). De la experiencia se deduce que un control proporcional produce un error estático: Una acción proporcional es proporcional al error, por lo que la respuesta es grande cuando el error es grande y corrige rápidamente, pero a medida que disminuye el error, la acción también decrece y llega un momento en que no es capaz de vencer la tendencia del proceso y se alcanza un equilibrio antes de alcanzar a la consigna. En el caso de la regulación de nivel, el nivel se mantiene cuando el caudal entrante y saliente se igualan. Puesto que la válvula de vaciado estará abierta, el caudal de salida no será cero y el de entrada tampoco podrá ser cero, ya que en el equilibrio han de ser iguales. Suponiendo que se consiguiera eliminar el error, la acción proporcional se haría cero y el caudal entrante también sería cero, pero como el caudal de salida es mayor que cero, el nivel bajaría (es imposible eliminar el error estático con acción proporcional).
figura 512.- Interesa un control únicamente proporcional:
| a) Nunca, porque no se puede eliminar el error estático. |
| b) Cuando se pueda hacer muy grande la constante Kp sin causar inestabilidad. |
| c) Cuando no existan perturbaciones. |
| d) Cuando el proceso sea lineal. |
Algunos procesos son muy estables y tienen muy poco retardo (por ejemplo el control de la presión de un gas), por lo que es muy difícil que aparezcan oscilaciones. En estos casos es suficiente con acción proporcional solamente, porque el parámetro Kp puede ser muy grande y el error estático muy pequeño. Cuando el error es grande, será necesario corregirlo mediante acción integral (regulador PI). Para este caso, calcularemos los parámetros con la segunda columna de la figura 4: Kp = 0.9 · T / (K · Tau) = 0.9 · 3.9 / (1.589 · 0.4) = 5.522; Ti = 3.33 · Tau = 3.33 · 0.4 = 1.332. Vacíe de nuevo el depósito con una consigna igual a cero y ponga estos valores en los campos para Kp y Ti, luego pulse en el potenciómetro de consigna bajo el valor 6 (por ejemplo) a la vez que pulsa la tecla G para dibujar la respuesta. El resultado será parecido al de la figura 6, donde se aprecia que ha desaparecido el error estático, se alcanza la consigna con rapidez y las oscilaciones ni siquiera son perceptibles. Cuando el error es grande, la acción proporcional es intensa y satura la señal de control (es de 10 voltios), por lo que el nivel aumenta con la máxima rapidez que permite el motor. Cuando falta poco para alcanzar la consigna, la señal de control decrece bruscamente para contrarrestar la tendencia creciente y posibilita un acercamiento progresivo, similar al frenado de un movil para detenerse en un punto exacto. Si la acción proporcional genera un error estático, la corrección del error es debida a la acción integral, pero, ¿cómo actúa la acción integral para conseguirlo?.
figura 6Un integrador acumula la señal que recibe, que en el regulador será el error (diferencia entre consigna y realimentación) y a medida que se acerca al valor de consigna irá creciendo la acción integral, porque el error es positivo. Cuando se hace pequeño, la acción proporcional se debilita pero la acción integral, que había estado creciendo, es la que se encarga de mantener la señal de control para eliminar el error. Cuanto más tiempo exista un error, más intensa se vuelve la acción integral y eliminarlo solo es cuestión de tiempo. En un regulador PID, la acción integral es más intensa cuanto más pequeño sea su parámetro Ti. Por esta razón, una acción integral se anula haciendo Ti muy grande. Este parámetro está relacionado con la acción proporcional, de hecho, Ti representa el tiempo (en segundos) que necesita la acción integral para ser tan intensa como la acción proporcional. En algunos reguladores se ajusta la acción proporcional con un factor Ki, en lugar de Ti. La relación que guardan es Ki = Kp / Ti, siendo Kp el parámetro de la acción proporcional. Si el parámetro es Ki en lugar de Ti, la acción integral se anulará haciendo cero Ki.
Pero no todo son ventajas cuando se recurre a una acción integral. Es cierto que elimina el error estático, pero también contribuye a inestabilizar la respuesta, especialmente en procesos con mucho retardo. En estos casos, el tiempo necesario para alcanzar a la consigna es grande y el error se acumula durante mucho tiempo. Cuando el error se anula, la acción integral es excesiva y se produce un rebasamiento, prolongándose las oscilaciones con bajo amortiguamiento o haciendo incluso inestable al proceso. La acción integral debe ser menos intensa cuanto mayor sea el retardo del proceso, lo que limita sus posibilidades de aplicación.
13.- Eliminar el error estático:
| a) Solo es posible con una acción integral en el regulador. |
| b) Se puede conseguir solo con acción proporcional si Kp es muy grande. |
| c) Se consigue con acción integral en el regulador pero también en algunos procesos con algún elemento integrador. |
| d) Solo es posible en procesos con poco retardo. |
Otra característica de los procesos es su inercia, entendida como su tendencia a mantener su reposo o actividad. Por ejemplo, cuando un movil de gran masa se acerca al final de su trayecto con alta velocidad, es necesario contrarrestar su tendencia anticipadamente para evitar el rebasamiento. Representando gráficamente la evolución de una magnitud, su inercia será tanto mayor cuanto mayor sea la pendiente de la gráfica. Pero la pendiente de una función es una derivada, por lo tanto, una forma de medir la inercia de una magnitud es valiéndonos de un elemento derivativo. Si añadimos al regulador una acción derivativa (regulador PID), calculamos los parámetros según la tercera columna en la figura 4, resultando: Kp = 1.2 · T / (K · Tau) = 1.2 · 3.9 / (1.589 · 0.4) = 7.363; Ti = 2 · Tau = 2 · 0.4 = 0.8 y Td = 0.5 · Tau = 0.5 · 0.4 = 0.2. Vacíe el depósito, ponga los datos calculados en el regulador y pulse en el potenciómetro de consigna bajo el valor 6 (por ejemplo) a la vez que pulsa la tecla G para dibujar la respuesta. El resultado debería parecerse a la figura 7, donde se comprueba que la acción derivativativa mejora la velocidad de respuesta, ya que el tiempo necesario para alcanzar a la consigna es menor de 4 segundos (la máxima velocidad de respuesta conseguida hasta el momento), no existe error estático y la respuesta es estable. Sin embargo, en la señal de control se aprecia una tendencia a producir saltos, aunque en la señal de realimentación son casi imperceptibles. Si nos fijamos, en la gráfica azul parecen existir oscilaciones amortiguadas con ruido superpuesto (una señal de alta frecuencia), como si se tratara de interferencias en una señal de radiofrecuencia.
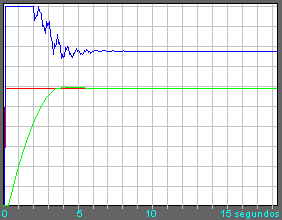figura 7Hay procesos en los que es perjudicial la acción derivativa porque es causa de una respuesta a saltos e irregular (por suerte, este efecto no ha sido exagerado en nuestro control de nivel). Cuando esto sucede, la acción derivativa deberá anularse y recurrir a un control PI. Para anular la acción derivativa basta con hacer igual a cero el parámetro Td. Este parámetro también guarda una relación con la acción proporcional, concretamente, Td es el tiempo (en segundos) que se necesita para que se igualen las acciones proporcional y derivativa cuando la señal aplicada es una rampa (recta ascendente). Es posible definir la acción derivativa con un factor Kd en lugar de Td, siendo la relación que existe entre ambos: Kd = Kp · Td donde Kp es el parámetro de la acción proporcional. Cuando la acción derivativa no es perjudicial, contribuye a reducir las oscilaciones debidas a la acción integral.
El selector que cambia de estado con la tecla D (en la simulación) tiene la función de seleccionar a qué se aplica la acción derivativa. Cuando se aplica a la señal de error (el contacto vertical), esta acción amplifica las pequeñas oscilaciones que proceden del sensor, por lo que es importante que los sensores sean de alta calidad. Si se cambia de estado el selector, la acción derivativa se aplica directamente a la señal del sensor a través de un filtro que reduce las interferencias (del sensor). Aplicado a la señal de error existe una desventaja: Cuando se produce un cambio brusco en la consigna, el error también varía bruscamente, pero inmediatamente se hace más constante y la acción derivativa satura un instante la señal de control para disminuir de nuevo bruscamente, originando un quiebro en la respuesta (que puede ser o no perceptible). Aplicado a la señal de realimentación, la acción derivativa cambia de signo por lo que en este caso se resta para obtener la señal de control en lugar de sumarse.
14.- Un quiebro en la respuesta cuando varía bruscamente la consigna se debe:
| a) A que el sistema tarda en reaccionar en el primer momento. |
| b) A que existe acción derivativa y está aplicada a la señal de error. |
| c) A que el error varía bruscamente en el primer momento pero luego se hace mucho más constante. |
SOLUCIONES:
1.- La apertura de vaciado no es indiferente, ya que cuanto menor sea, primero comienza a reaccionar el nivel. Puede ser importante que no se desborde el depósito, pero esto podrá evitarse con una acción de control adecuada. Si cierra total o parcialmente la válvula, se puede comprobar que el margen de funcionamiento admisible es más amplio (entre 2.5 y 10 voltios más o menos), por lo que el caso más desfavorable aparece con la válvula completamente abierta (correcto c).
2.- Velocidad mínima para subir el líquido hasta el depósito: Si a 10 voltios corresponden 3000 rpm, a 4 voltios corresponden 1200 rpm (correcto b)
3.- Si el sistema está bien diseñado, las alturas de elevación son correctas. Si entra aire en el conducto la bomba trabajará en vacío y no eleva el líquido, luego la "c" puede ser correcta. Si el antirretorno no cierra, el depósito se vacía a través de la bomba y si el aire llega a la bomba estaremos en el mismo caso anterior, luego la "d" puede ser correcta. Si la rejilla está obstruída no puede entrar el líquido, luego la "e" también puede ser correcta.
4.- En una bomba centrífuga, la altura máxima de elevación depende del número de revoluciones. Esta velocidad es proporcional a la señal de mando, que al mantenerse constante, también se mantiene la velocidad. A medida que el nivel aumenta, la diferencia entre niveles máximo y real disminuye, por lo que el caudal de entrada disminuye. A la vez, al aumentar el nivel aumentará el caudal de salida. Si el de entrada disminuye y el de salida aumenta, llega un momento en que se igualan y el caudal resultante es cero, en cuyo momento el nivel se mantiene (correcto c). Si se alcanzara la altura máxima de elevación, el caudal entrante sería cero, pero esto no es posible porque ha de ser igual al caudal de salida, que no es cero por estar la válvula abierta.
5.- Una regulación en lazo cerrado tiene que haber sido ajustada alguna vez. También es posible que se modifiquen características del proceso y sea necesario ajustar de nuevo. Para hacer determinadas mediciones o ajustes, es posible que haya que hacer funcionar el proceso en lazo abierto, luego es normal que pueda funcionar de ambas formas. Puesto que acaba de pasar el proceso a lazo cerrado, seguramente habrá comprobado que el depósito se vaciaba rápidamente. Supongamos que se trata de una mezcla de agua y ácido cítrico, por lo que al disminuir la concentración de agua, resultará una mezcla demasiado ácida y la producción será defectuosa. No basta con vigilar el proceso porque nuestra reacción puede llegar demasiado tarde. Antes de cambiar el modo de funcionamiento, hay que asegurarse de que la señal de mando del actuador (el variador en la simulación) no sufrirá alteraciones importantes (correcto b).
6.- En este momento, el regulador tiene todas las acciones anuladas y su salida de control es cero, por lo tanto no está ajustado (correcto b).
7.- Con 0 metros (vacío) la señal es 0 voltios y con 8 metros la señal es 10 voltios, luego hay una variación de nivel igual a 8 metros cuando la señal del sensor tiene una variación de 10 voltios. La ganancia será 10 volt. / 8 metros = 1.25 volt./m (correcto a).
8.- Si no es autorregulable no se estabiliza la variable regulada (en lazo abierto). Si es autorregulable con perturbaciones sí se estabiliza, pero no se mantiene constante. Es necesario que sea autorregulable y sin perturbaciones para mantener la variable regulada constante (correcto c). Existen determinadas excepciones como es la conducción de vehículos, en los que la dirección se regula en lazo abierto (girando el volante), pero se trata de casos muy difíciles de regular automáticamente, en los que de momento se tiene más éxito con el aprendizaje y la experiencia. Otra excepción son determinados actuadores, que por sus características son casi insensibles a las perturbaciones, este puede ser el caso de los motores de corriente alterna, en los que al aumentar el par resistente aumentan el par motor y mantienen así una velocidad con pequeñas variaciones.
9.- Excepto en los osciladores, el tiempo de estabilización debe ser mínimo (correcto a). Unas veces lo más importante es una rápida respuesta (correcto c) y otras una buena precisión (correcto f). En todo caso, la variable regulada ha de ser estable, oscilando lo menos posible al alcanzar a la consigna (correcto d). En lazo abierto, el actuador debe ser lo menos sensible posible a las perturbaciones, pero no es fundamental en lazo cerrado porque se basa en comprobar el error (entre consigna y realimentación) y corregirlo. La medida del sensor (realimentación) debe ser muy precisa y estable en lazo cerrado, porque los errores de medida influyen de manera importante en la respuesta del regulador (correcto g). De hecho, el sensor es el elemento crítico en toda regulación en lazo cerrado.
10.- Es claro que lo ideal es el modelo matemático, pero los reguladores están diseñados para adaptarse a múltiples procesos y solo en casos excepcionales se diseñan para una aplicación concreta. Algunos reguladores aprenden verdaderamente del proceso, pero son sistemas demasiado complicados para aplicaciones corrientes. Se basan en una red neuronal artificial cuyas neuronas ajustan automáticamente sus "pesos" en función de una ley de aprendizaje. Estos sistemas entroncan con la llamada "inteligencia artificial" entre cuyas disciplinas está teniendo gran aceptación la "lógica difusa". Sin embargo, se trata de sistemas que desbordan el alcance de los reguladores industriales. Lo que sí debe hacer un regulador es anticiparse a las desviaciones para corregirlas antes incluso de que aparezcan (correcto d).
11.- Según la figura 3 y el cálculo según la figura 2, Y2 - Y1 será 6.514 - 0.0157 = 6.357 voltios. X2 - X1 = 8 - 4 = 4 voltios. El 63.2% de Y2 - Y1 es 0.632 · 6.357 = 4.0176 voltios. Para este valor, el tiempo T2 resulta 4.3 segundos (gráfica de figura 3). El 28.3% de Y2 - Y1 es 0.283 · 6.357 = 1.799 voltios. Para este valor, el tiempo T1 resulta 1.7 segundos (gráfica de figura 3). La ganancia K = (Y2 -Y1) / (X2 - X1) = 6.357 / 4 = 1.589. La constante de tiempo T = 1.5 · (T2 - T1) = 1.5 · (4.3 - 1.7) = 3.9 segundos. El tiempo muerto Tau = T2 - T = 4.3 - 3.9 = 0.4 segundos (correcto c).
12.- Es suficiente con una acción proporcional cuando el error estático sea aceptable (pequeño), lo que se consigue con un valor Kp grande, siempre que esto no cause oscilaciones mal amortiguadas. Estas condiciones se cumplen en procesos con poco retardo (correcto b).
13.- El error solo se elimina con algún componente integrador, que también puede formar parte del proceso (correcto c).
14.- Un quiebro en la respuesta se deberá a un salto momentáneo de la señal de control, que a su vez puede ser debido a un pico brusco de la acción derivativa si está aplicada a la señal de error (correcto b).