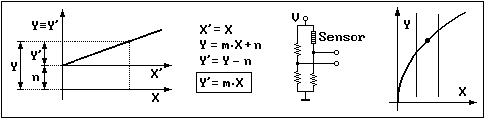TEORÍA DEL REGULADOR PID.
El comportamiento de un regulador guarda una estrecha relación con el proceso que controla, hasta el punto
que será imposible analizar cada cosa por separado. Conocer los procesos es entonces un fundamento que
no debemos ignorar, puesto que el propio regulador es una parte integrada en los mismos. La regulación puede
estar apoyada en una fuerte base matemática que aquí solo se menciona. Nuestro objetivo solo es aprender
cómo regular, centrándonos en una comprensión intuitiva de los procesos.
Procesos lineales y no lineales.
Se dice que un proceso es lineal cuando está formado por componentes que dan una salida proporcional a su
entrada. Su representación gráfica es una recta que pasa por el origen de coordenadas tal y como puede verse
en la figura. Son muchos los componentes que pueden considerarse lineales, por ejemplo una palanca para
la que se considera como entrada la fuerza aplicada en uno de sus extremos y como salida la fuerza que se
desarrolla en el extremo opuesto, un amplificador (cuya salida es la tensión de entrada multiplicada por una
constante), etc.
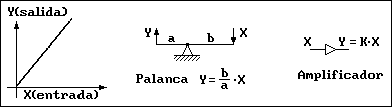
Como casi la totalidad de los reguladores, el PID es también un regulador lineal y aunque existen numerosos
procesos que no son lineales, resulta más sencillo linealizarlos o aproximarlos a procesos lineales en lugar de
utilizar reguladores no lineales, que son mucho más difíciles de ajustar, son muy complejos, o exigen un modelo
matemático del proceso muy fiable. Las señales que con más frecuencia necesitan ser linealizadas son las
que proceden de elementos sensores. Cuando el regulador es digital será posible hacerlo por programa,
aunque supone una carga adicional para el procesador. También puede recurrirse a determinados
componentes capaces de sumar o restar señales, hacer la raíz cuadrada..., e incluso a generadores de
funciones a medida, que normalmente son programables. Actualmente es mayor la tendencia a incluir dentro
del sensor la electrónica necesaria para la adaptación de la señal, pudiendo incluso disponer de sensores
programables capaces de establecer comunicaciones muy evolucionadas.
En la siguiente figura se representa una respuesta que aunque no es lineal se transforma fácilmente en lineal
restando la ordenada en el origen (n) a la señal de salida del componente, lo que puede hacerse por programa
o mediante un elemento capaz de restar dos señales. Como ejemplo de componente que requiere este tipo de
tratamiento puede ser cualquier sensor tipo puente que nos da una medida por comparación con un valor de
referencia. En el ejemplo de la figura debe restarse la tensión entre los dos terminales de salida para obtener
un valor representativo de la medida.
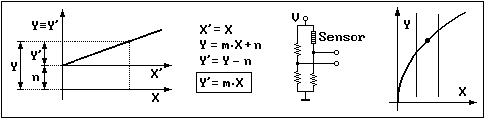
Cuando la representación gráfica de la entrada y salida de un componente es una curva (figura anterior), puede
recurrirse a diversas técnicas de linealización. La más sencilla implica aceptar que la regulación solo será
buena cuando el proceso se acerca a un punto de funcionamiento óptimo y hacerlo trabajar siempre en sus
proximidades, de forma que se pueda considerar sin mucho error que la respuesta es una recta tangente a la
gráfica en el punto de funcionamiento escogido. Otra forma sería transformar la curva en una recta mediante un
elemento apropiado (conviene conocer el modelo matemático de la respuesta del componente) o por
programa, o bien con un generador de funciones en el que se programan un conjunto de puntos.
Diagramas de bloques.
La representación de los procesos continuos se hace por bloques que simbolizan a un componente o conjunto
de componentes. La transformación que se produce en cada bloque, convirtiendo la señal de entrada en la de
salida, puede caracterizarse por el componente, de igual forma que vimos en el control en lazo abierto y cerrado.
Matemáticamente, cada bloque se identifica por una función de transferencia que representa la ganancia del
bloque, de forma que la salida es igual a la entrada multiplicada por la ganancia del bloque. Con las funciones
de transferencia es posible simplificar todo el proceso en un solo bloque y la función de transferencia que
resulta es el punto de partida para estudiar la estabilidad, rapidez de respuesta y otras especificaciones que
podrán ser exigidas. La función de transferencia es una forma abstracta y general para estudiar la regulación de
un proceso, independiente de los elementos físicos que producen la transformación.
Todo proceso admite ser representado con un número reducido de bloques característicos sin que resulte
necesario saber de qué componente se trata. En la siguiente figura podemos ver el conjunto de bloques según
su representación gráfica, todos ellos constituyen la salida del bloque cuando se introduce a su entrada un
escalón unitario (señal que pasa de 0 a 1 en un instante).
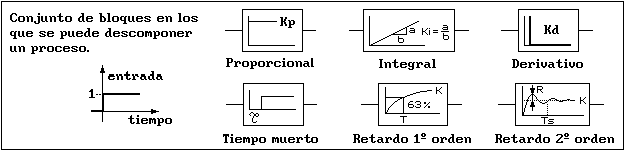
Bloque proporcional: Multiplica el valor de entrada por una constante que
representa su ganancia (Kp). Como consideramos una entrada unitaria, la salida toma el valor Kp. Si Kp es
mayor de 1 se comporta como un amplificador y si es menor de 1 lo hará como un atenuador. Como ejemplos
de componentes que se comportan de esta manera encontramos muchos transductores y los amplificadores
de tensión, de potencia, etc.
Bloque integrador: Su salida es la integral de la señal de entrada. Una integral es
el área bajo la curva de una función, y aunque matemáticamente suele ser un cálculo complejo, su determinación
gráfica puede facilitar su comprensión en muchas ocasiones. Si la entrada es unitaria (y constante), la integral o
área será igual a 1 multiplicado por el tiempo transcurrido, puesto que se trata de un rectángulo (ver siguiente
figura). La respuesta del bloque es por lo tanto igual al tiempo multiplicado por una constante integral Ki, que
representa la pendiente de una recta. Como ejemplos tenemos un depósito para el que consideramos como
entrada un caudal y como salida el nivel alcanzado por el líquido, también la tensión de un condensador cuando
se le carga con una intensidad constante, la temperatura de un recinto aislado al aplicar una fuente de energía
constante, etc. En general, se considera un integrador cualquier elemento que acumula la magnitud de entrada.

Bloque derivador: Su salida es la derivada de la señal de entrada. La derivada de
una función en un punto es la pendiente que tiene la recta tangente a la función en dicho punto. En la figura
anterior se indica este concepto. Como se considera como entrada un valor que pasa de cero a uno de forma
instantánea, la pendiente en ese instante es infinito e inmediatamente se anula porque la entrada se mantiene
constante (la pendiente de una horizontal es cero). Un ejemplo típico de un comportamiento derivador es un
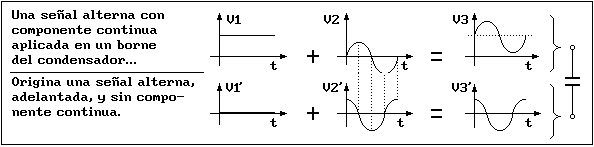
condensador conectado en serie, capaz de eliminar la componente continua (constante) de una corriente
alterna (véase la figura siguiente, en la que las gráficas inferiores corresponden exactamente con las funciones
derivadas de las superiores). Otro ejemplo puede apreciarse en la visión de algunas serpientes, que son
prácticamente ciegas en ausencia de movimiento pero "ven" perfectamente algo que se mueve.
Bloque tiempo muerto o retardo puro: La salida es igual a la entrada pero
retardada un tiempo (tau) determinado. En realidad no son frecuentes en regulación elementos que se
comportan de esta forma (son una importante causa de inestabilidad), pero prácticamente todos tienen una
respuesta en la que interviene en mayor o menor grado un retardo puro.
Bloque retardador simple o de primer orden: La salida alcanza el valor de la
entrada después de un cierto tiempo, pero no de forma instantánea sino que tiende a seguir a la entrada desde
el primer instante. Generalmente aplica una ganancia K determinada, es decir, la salida termina alcanzando el
valor de entrada multiplicado por esa constante K. El tiempo que tarda en alcanzar el 63% del valor final se
denomina constante de tiempo T y alcanza prácticamente el valor final (95%) en un tiempo 3T. Como ejemplos
puede citarse el caudal de salida de un depósito, que va creciendo cada vez más despacio hasta igualarse
con el caudal de entrada. También la velocidad de un motor de corriente continua de imanes permanentes
respecto de la tensión de entrada en el inducido, o la tensión de salida de un circuito RC (entre extremos del
condensador) respecto de la tensión de alimentación. En general, ocurre con la mayoría de los sistemas con
una inercia que se opone a las señales de entrada.
Bloque retardador de segundo orden: Así se comportan los elementos que
almacenan energía y la devuelven con retraso, produciendo una oscilación. Como se observa en la figura de
este bloque al principio del apartado, R es el rebasamiento máximo, K es la ganancia del elemento, Ts es el
tiempo necesario para alcanzar un régimen de equilibrio, entendiendo como tal el tiempo a partir del cual el
error está dentro de una tolerancia de +2 y -2% del valor final. Un ejemplo de sistema retardador de segundo
orden es el conjunto masa-muelle-amortiguador: El muelle acumula la energía cinética de la masa y la devuelve
con retraso; el amortiguador origina la disminución de la oscilación por el rozamiento fluido. Otro ejemplo es el
circuito RLC, que produce una tensión entre los extremos del condensador de una forma oscilante y
amortiguada cuando se aplica bruscamente una tensión de alimentación.
Simplificación de bloques.
En ocasiones podremos hacer simplificaciones de forma intuitiva, siempre considerando que se aplica a la
entrada un escalón unitario. Veamos tres ejemplos:
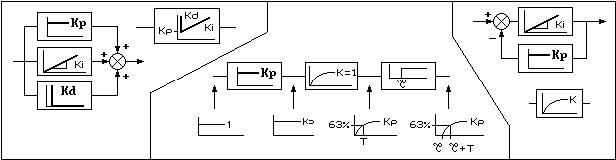
Los efectos de varios bloques en paralelo se suman. En el primer caso de la figura anterior la salida es infinito
al principio, un instante después la suma es igual a Kp y posteriormente, el valor Kp se suma a la señal del
bloque integrador, lo que equivale a elevar la recta paralelamente sobre sí misma un valor Kp. También pueden
restarse valores. Los efectos de varios bloques en cascada (en serie) afectan al resultado obtenido en el
bloque anterior. En el segundo caso de la figura anterior puede comprobarse que el efecto que corresponde a
cada bloque se superpone a la gráfica de la salida del bloque anterior. Esto será cierto siempre y cuando el
comportamiento de cada bloque no se vea afectado por la conexión con el siguiente. Un ejemplo en el que no
es cierto puede ser cuando se alimenta un motor de corriente continua a través de un divisor de tensión con
resistencias, porque el motor constituye una carga que afecta a la tensión de salida del divisor. Con bloques en
lazo cerrado es difícil de interpretar generalmente. En el tercer caso de la figura anterior la salida aumenta
linealmente al principio, pero a medida que va creciendo se irá restando también un valor proporcional a la
salida y el crecimiento será cada vez más lento hasta que la salida se mantenga constante. El conjunto se
comporta como un bloque retardador de primer orden.
La simplificación matemática de bloques se basa en las funciones de transferencia, reduciendo todo el conjunto
a un solo bloque con una sola función. Nos limitaremos a ver las funciones que corresponden a los tipos de
bloques que se han descrito, sin entrar en más detalles:

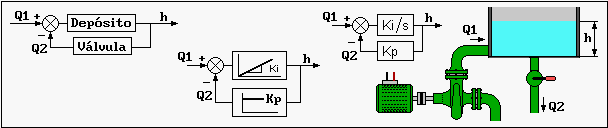
En la figura siguiente podemos ver el diagrama de bloques que corresponde a un depósito con un caudal de
entrada y otro de salida. El conjunto es equivalente a un depósito sin salida en el que entra un caudal igual a la
diferencia entre los dos caudales, por lo que se comporta como un acumulador (el comportamiento se
corresponde con un bloque integrador). Es claro que al aumentar el nivel, el caudal Q2 también aumenta, por lo
que la válvula de vaciado se comporta de forma parecida a un bloque proporcional. Aunque esta semejanza no
es del todo cierta en la práctica (el caudal no es proporcional al nivel sino a su raíz cuadrada), la aproximación
es aceptable si el nivel no sufre grandes variaciones respecto del punto de equilibrio, es decir, la regulación
podrá ser buena en cierto margen de variación del nivel. Como ya se justificó anteriormente, este conjunto de
bloques se reduce a un solo bloque con retardo de primer orden.
Regulador PID.
Como ya sabemos, no se trata de un dispositivo concreto sino de una forma muy habitual de comportarse un
regulador, ya sea éste analógico o digital. Ténganse en cuenta las ideas expuestas en la introducción sobre
el PID pues en este apartado se consideran conocidas.

En la figura anterior vemos el diagrama de bloques correspondiente al PID y la representación matemática de
la señal de control, que es la suma de las tres acciones ya conocidas, es decir, un valor proporcional al error,
mas la constante integral Ki por la integral del error, mas la constante derivativa Kd por la derivada del error.
Las acciones integral y derivativa no se ajustan generalmente por sus constantes sino por un tiempo integral Ti
y un tiempo derivativo Td que dependen de la constante proporcional (Kp), quedando la expresión que
aparece en la zona inferior de la figura.
Modificaciones en el regulador básico:
Los cambios bruscos en la consigna son la causa de una variación rápida del error y la acción derivativa
satura la salida de control en el primer instante. Por este motivo la respuesta del sistema experimenta un
quiebro poco favorable como puede haber comprobado ajustando el PID del apartado sobre la práctica con
el regulador. El inconveniente explicado hace aconsejable que la acción derivativa no se calcule directamente
con el error si pueden existir cambios bruscos en consigna. En su lugar, puede calcularse a partir de la señal
del sensor como se verá en la siguiente figura.
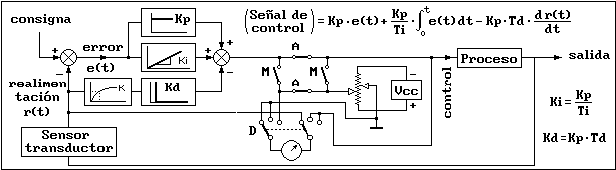
Suponiendo nula la consigna es claro que la señal de error es igual pero opuesta a la señal del sensor r(t).
Debido a que ahora la acción derivativa actúa sobre la señal del sensor se ha cambiado el signo + por el signo
menos en el término derivativo. Otra modificación frecuente en el PID básico se debe a que la señal de salida
de los sensores puede ser afectada por ruido externo que luego es amplificado por la acción derivativa (o
simplemente perturbaciones que origina el propio sensor). Para evitar este problema se filtra la señal del
sensor de forma que se transmitan las frecuencias bajas pero se eliminen las altas. Esto se puede conseguir
con un filtro pasabajos, que puede ser cualquier elemento cuya respuesta corresponde a un retardo de primero
o segundo orden (si las señales son eléctricas, un filtro pasabajos puede ser simplemente una resistencia en
serie y un condensador en paralelo). En la figura anterior existe un sistema de equilibrado manual que permite
abrir el lazo de regulación para actuar manualmente sobre el proceso. El indicador (un voltímetro) permite
visualizar las señales que serán importantes para determinar experimentalmente los parámetros del regulador
y para comprobar si es posible el paso entre el modo automático y manual.
Los interruptores A y M (figura anterior) siempre tienen estados opuestos, cuando A está cerrado tendremos
regulación automática y cuando es M el que está cerrado la regulación será manual. El cursor derecho del
potenciómetro va conectado a la masa del regulador, así es posible (con el cursor izquierdo) establecer una
señal manual por encima o por debajo del nivel de referencia (masa). Un conmutador (D) con tres posiciones
sirve para seleccionar la señal que llegará al voltímetro. En la primera posición (la dibujada) veremos la
señal del sensor r(t), en la segunda veremos la señal de control, que dependiendo de A y de M procederá del
regulador o del potenciómetro manual, y en la tercera posición estaremos midiendo la diferencia entre la señal
del regulador y la del potenciómetro manual. Esta última posición es importante para que al pasar del modo
automático al manual (o al contrario) no se produzca una reacción brusca que pudiera ser difícil de controlar.
Antes de ejecutar el paso de un modo al otro ajustaremos el potenciómetro hasta conseguir que el indicador
marque cero (con D en la tercera posición).
Otra función que suele ser conveniente es la aplicación de consignas en rampa y en escalón con el propósito
de hacer pruebas para el ajuste del regulador. Naturalmente, esta y otras funciones posibles pueden estar
automatizadas, por ejemplo para cambiar en cualquier momento entre el modo automático y manual sin
preocuparse de ajustar a cero una indicación.
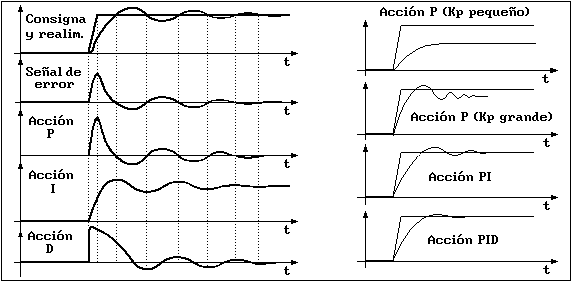
En la parte izquierda de la siguiente figura podemos ver cómo responden las tres acciones del regulador y a la
derecha ejemplos de la respuesta que se consigue con la acción P solamente o combinando varias acciones.
Los puntos de la gráfica del error se obtienen restando la señal de consigna y la de realimentación. La acción
P es igual al error pero amplificado o atenuado dependiendo de la constante Kp. La acción I aumenta mientras
el error es positivo y disminuye cuando es negativo (se va sumando el área por encima de cero y se va
restando el área negativa), tendrá un máximo o un mínimo cada vez que el error se anula y se comprueba que
al estabilizarse mantiene un valor no nulo. La acción D no actúa sobre el error sino sobre la realimentación y
como ya se explicó, es la pendiente de la recta tangente a la gráfica de la señal de realimentación. Cuando la
tangente es horizontal, la pendiente es cero y la acción D también, cuando la recta tangente es creciente o
decreciente, la pendiente es positiva o negativa respectivamente y la acción D responede de igual forma. Si
actúa solamente la acción P y su constante Kp es pequeña se mantiene un error considerable porque a
medida que el error disminuye también decrece la acción P hasta que llega un momento en el que no puede
vencer la tendencia del proceso. Con acción P y la constante grande se aminora el error pero se acentúan las
oscilaciones, pudiendo llegar a inestabilizar el proceso. La acción integral no se utiliza nunca sola porque
origina oscilaciones muy grandes que hacen fácilmente al sistema inestable, pero combinada con la acción P
es muy indicada para procesos autorregulables, siendo la mayoría de los industriales de este tipo. Cuando la
acción P ya no es capaz por sí sola de anular el error, la acción integral estará ayudando gracias al error
acumulado y en unas pocas oscilaciones el error será prácticamente nulo. Si Kp y Ti son adecuados para el
proceso las oscilaciones serán mínimas. En los procesos en los que la acción D no sea perjudicial, la
combinación de las tres acciones aportará una respuesta rápida que además alcanza el régimen de equilibrio
en poco tiempo. Observando las gráficas de las acciones integral y derivativa se comprueba que tienen igual
signo pero como la acción derivativa se resta, hace que disminuyan las oscilaciones que causa la acción
integral. Puesto que la acción D se estabiliza con valor 0, la combinación de ambas mantiene un valor que no
es nulo, lo que demuestra que la acción derivativa contribuye a eliminar las oscilaciones de la acción integral
sin impedir que se anule el error.
Otras modificaciones:
PID error cuadrático: Puede especificarse que un controlador actúe
enérgicamente cuando se producen grandes desviaciones del punto de consigna y que sea poco sensible
para las pequeñas. Una solución consiste en multiplicar a su expresión matemática por otra función
f(e) = m+(1-m)·e donde e es la señal de error y m un parámetro. Si m es cero equivale a una ley cuadrática del
error y si m es 1 no afecta para nada. Normalmente se le da el valor m=0,1 que mejora la salida frente a
perturbaciones en la medida y alcanza más eficazmente la consigna, pero produce mayores oscilaciones con
el efecto de las perturbaciones del proceso.
PID+Todo o nada: Cuando el error se encuentra entre los límites +m y -m
(parámetro adicional para este regulador) actúa normalmente la acción PID. Cuando se rebasa, el
comportamiento pasa a ser de tipo todo o nada. Este controlador garantiza la máxima velocidad de respuesta
frente a variaciones rápidas de consigna (el error es grande y actúa el control todo o nada) y permite la acción
PID clásica cuando la variable de salida se acerca al valor de consigna.