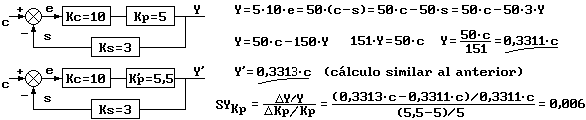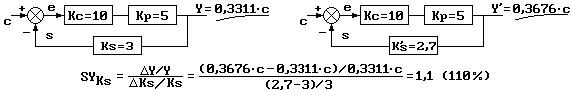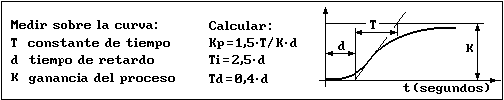TEORÍA DEL REGULADOR PID.
Parámetros del regulador PID.
Son la constante o ganancia proporcional (Kp), el tiempo integral (Ti) y el tiempo derivativo (Td). En lugar de
indicar la constante proporcional se da en ocasiones la banda proporcional expresada en tanto por ciento, se
calcula como la inversa de la constante proporcional y multiplicado por 100. El tiempo integral representa el
tiempo que necesita la acción integral para suministrar una señal igual a la proporcional. Si el error es un
escalón, la acción P será una horizontal y la acción I será una recta creciente. La suma será otra recta con igual
pendiente pero elevada una distancia igual a la acción P. Cuando ha transcurrido un tiempo igual a Ti, las
acciones proporcional e integral serán iguales, de donde se deduce la relación que se indica en la figura
siguiente. Cada vez que la acción integral alcanza a la proporcional se dice que se ha producido una repetición
y Ti se expresa en minutos o segundos por repetición. A veces se indica la inversa de Ti, quedando expresado
en repeticiones por minuto o segundo. Debe tenerse en cuenta que la acción integral disminuye al aumentar Ti,
de forma que para anular esta acción tendrá que darse a Ti un valor muy grande.

Si la señal de error aumenta linealmente con el tiempo (una señal en rampa), la acción P será igualmente una
recta con mayor o menor pendiente dependiendo del valor de Kp. Debido a que la pendiente del error es
constante, la acción derivativa será una recta horizontal. La acción combinada PD aparenta ser una acción
proporcional que se anticipa Td unidades de tiempo. Td se mide en segundos o minutos. Cuando ha pasado
un tiempo igual a Td, las acciones proporcional y derivativa son iguales como vemos en la perte derecha de la
figura anterior, de ello se deduce la relación entre Td y Kp. La acción derivativa aumenta si el valor Td aumenta,
de forma que para anular esta acción tendrá que darse a Td el valor cero.
Precisión estática de un control en lazo cerrado.
Se define como la relación entre las señales de error y de consigna cuando se ha alcanzado el equilibrio y se
multiplica por 100 para expresarlo en tanto por ciento. Vamos a llamar Kc a la ganancia del controlador en
régimen estático (en equilibrio), Kp a la ganancia del proceso y Ks a la ganancia del sensor.

Proceso autorregulable con controlador proporcional:
En este ejemplo la precisión no es buena, luego existe un error estático que no se anula y constituye un 14,3%
del valor de consigna.

Proceso no autorregulable con controlador proporcional:
En este caso tenemos un bloque integrador que no permite en lazo abierto alcanzar el equilibrio (sistema no
autorregulable). El bloque integrador no tiene propiamente una ganancia estática porque el valor de su salida
tiende a infinito con el tiempo cuando se le aplica una entrada constante. El resultado de 0% (ejemplo de la
figura) indica que la salida seguirá fielmente a la consigna en régimen estático, aunque no nos da información
sobre el comportamiento antes del equilibrio ni tampoco sobre el tiempo necesario para alcanzarlo.

Proceso autorregulable con controlador PI:
A diferencia del primer ejemplo, vemos que añadiendo una acción integral en el controlador se elimina el error
estático en un proceso autorregulable.

Precisión estática con perturbaciones.
Es frecuente que un sistema en lazo cerrado esté influido por perturbaciones que forman parte del proceso. Si
el sistema es lineal, el valor de una señal se puede calcular como la suma de los efectos que originan las
acciones que intervienen por separado. Así pues, para determinar el error correspondiente a la figura
hallaremos un primer error (e´) originado solamente por la consigna (con perturbación "t" igual a cero), un
segundo error (e´´) causado solamente por la perturbación (con la consigna igual a cero) y sumaremos los
resultados. Consideramos Kp1 la ganancia del proceso antes de la perturbación y Kp2 la ganancia del proceso
después de la perturbación.

Proceso autorregulable con controlador proporcional:
En el primer ejemplo del apartado anterior se vió el mismo caso pero sin perturbaciones, donde se justificó
que la precisión ni era buena. Introduciendo una perturbación de valor 7 (figura siguiente), la precisión es aún
peor, ya que aumenta de 14.3 a 34.3 %.

Proceso no autorregulable con controlador proporcional:
En el segundo ejemplo del apartado anterior se vió el mismo caso pero sin perturbaciones, donde se justificó
una perfecta precisión estática. Si introducimos una perturbación de valor 7 (figura siguiente), el sistema deja
de responder de manera precisa.

Proceso autorregulable con controlador PI:
En el tercer ejemplo del apartado anterior se vió el mismo caso pero sin perturbaciones, donde se justificó
una perfecta precisión estática. Si introducimos una perturbación de valor 7 (figura siguiente), el sistema sigue
manteniendo su precisión. Se constata que un regulador con acción integral permite que la salida de un
proceso autorregulable siga fielmente a la consigna en régimen estático, haya o no haya perturbaciones.

Sensibilidad de un proceso.
Interesa que la salida de un sistema sea insensible a la variación de sus parámetros para evitar problemas
debidos a la imprecisión de sus componentes, o incluso por falta de linealidad de los mismos. Se define la
sensibilidad como el cociente entre la variación unitaria de la salida entre la variación unitaria del parámetro
respecto del cual deseamos calcular la sensibilidad.

Sensibilidad respecto de la ganancia del proceso en lazo abierto:
Suponemos que la ganancia del proceso (Kp) vale 5 inicialmente y se incrementa hasta 5,5. Consideramos la
ganancia del controlador Kc=10. El cálculo que se desarrolla a continuación indica que la salida se incrementa
en la misma proporción que lo haga la ganancia del proceso (100%), razón por la que es tan impreciso este
control).

Sensibilidad respecto de la ganancia del proceso en lazo cerrado:
Suponemos que Kp pasa igualmente de 5 a 5,5. El cálculo que se desarrolla a continuación indica una
sensibilidad de solo un 0,6%, que es mucho más interesante.
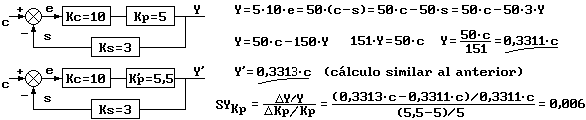
Sensibilidad respecto de la ganancia del sensor en lazo cerrado:
Suponemos que la ganancia del sensor pasa de 3 a 2,7. El resultado del cálculo que a continuación se
desarrolla deja bastante que desear, razón por la que resulta muy importante adquirir sensores con una
ganancia muy estable y se justifica que los sensores son realmente la clave del éxito de una buena
regulación.
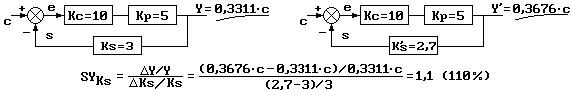
Orientaciones para el uso del regulador PID.
Para el control de posición o dirección , velocidad y aceleración, se utilizan las tres
acciones, aunque existen algunas excepciones como el control numérico de máquinas en las que se aplica el
regulador P para el control de la posición de la herramienta y un regulador PI para el control de la velocidad de
la misma.
En la regulación del caudal y presión en líquidos es esencial la acción integral pero perjudicial la derivativa
porque amplifica las perturbaciones que producen los sensores de medida de este tipo de variables. Por lo
tanto se recomienda un PI con un tiempo integral elevado. Para la regulación de nivel ocurre lo mismo aunque
puede prescindirse de la acción integral si el error es aceptable.
Es esencial la acción derivativa en la regulación de temperatura porque los retardos son considerables, pero
es innecesaria en la regulación de la presión de un gas para la que basta con un controlador proporcional con
una ganancia grande. La variación de la presión es un proceso muy estable y se elimina prácticamente el error
con una acción P.
Es necesaria la acción integral si el proceso es continuo pero no lo es si el propio proceso dispone de un
elemento integrador (control P o PI). En la regulación de temperatura y presión de vapor es necesaria la acción
integral y la derivativa es esencial si se necesita acelerar la respuesta. En la regulación del pH es esencial la
acción integral y la derivativa es recomendable.

Sintonía de parámetros del regulador PID.
El primer paso para aplicar un controlador consiste en elegir el tipo adecuado (P, PI, PID), para lo cual se
necesita comprender el efecto de las tres acciones y a ser posible tener experiencia sobre el proceso a
controlar. El segundo paso es ajustar los parámetros para que la respuesta del sistema se ajuste a unas
determinadas especificaciones.
El ajuste de parámetros es frecuente en procesos industriales, no solo en los trabajos de puesta en marcha,
sino también cuando se detectan cambios sustanciales del comportamiento del proceso. Las técnicas
experimentales están especialmente orientadas al mundo industrial, donde existen grandes dificultades para
obtener una descripción matemática. Las técnicas de ajuste son:
- Prueba y error. Se necesitan unos criterios básicos y largo tiempo de ensayo.
- Sintonía en lazo abierto. Experimental.
- Sintonía en lazo cerrado. Experimental.
- Sintonía con especificaciones frecuenciales. Experimental.
- Sintonía analítica. Requiere modelo matemático fiable.
La primera de las técnicas ya fué explicada y experimentada en el apartado de la práctica con PID. A
continuación veremos la segunda y tercera técnica, pero no las dos últimas. Las especificaciones de
funcionamiento que se pueden imponer en un proceso están sujetas a diversas limitaciones, por ejemplo con
un controlador proporcional sería incompatible pedir a la vez la máxima precisión y la máxima estabilidad
porque la mejora de una de ellas origina un perjuicio en la otra. Estas son las especificaciones más
frecuentes:
- Tiempo de respuesta, que será el máximo aceptado para que se alcance el
equilibrio después de un cambio de la consigna.
- Precisión estática, cuyo significado ya conocemos.
- Banda pasante, que es la gama de frecuencias para las que el sistema debe
responder sin una pérdida excesiva de su ganancia.
- Margen de fase y margen de ganancia, que constituyen una medida de la
estabilidad del sistema.
Sintonía de parámetros en lazo abierto.
Esta técnica solo puede aplicarse con procesos autorregulables (la mayoría de los industriales) porque se
necesita alcanzar un equilibrio en lazo abierto para medir las constantes del proceso. El comportamiento de los
procesos autorregulables puede interpretarse como la conexión en cascada de un bloque de retardo puro, con
un tiempo de retardo tau, y un bloque retardador de primer orden con una constante de tiempo T y una ganancia
K.

Los pasos para determinar los parámetros Kp, Ti y Td son los siguientes:
1.- Poner al proceso en lazo abierto, para lo cual será bueno disponer de un
sistema que facilite esta operación y permita la medida de la consigna manual y la señal del sensor.
2.- Ajustar el offset y la ganancia del sensor si no se ha hecho antes para que su
banda de variación coincida con la de consigna. Primero se ajusta el cero mediante el mando de offset y a
continuación se fija el límite superior con el ajuste de ganancia.
3.- Buscamos que la salida se estabilice en un valor cualquiera que llamamos Y1
y anotamos el valor de consigna que hemos ajustado para conseguirlo y que podemos llamar X1 (los valores
X1 e Y1 definen un primer punto de equilibrio). Buscamos un segundo punto de equilibrio que estará definido
por otra pareja de valores (X2 e Y2). Estas operaciones pueden llevar largo tiempo de espera, dependiendo del
tipo de proceso.
4.- Calculamos la ganancia del proceso (K) como se indicó en la figura anterior.
5.- Ajustamos la consigna en el valor X1 que tendremos anotado y esperamos el
equilibrio, que lógicamente se alcanzará cuando la salida llegue al valor Y1.
6.- Ajustamos la consigna en el valor X2 y medimos los tiempos T1 y T2 que
corresponden al 28,3% y al 63,2% de la variación que experimentó la salida y que podemos ver reflejado en la
figura anterior.
7.- Calculamos la constante de tiempo del proceso (T) y el tiempo de retardo (tau)
de la forma indicada en la figura anterior.
8.- Con los tres parámetros del proceso ya conocidos (K, T y tau) podremos
calcular los parámetros del PID (Kp, Ti y Td) según el criterio de funcionamiento que nos parezca más
adecuado. Estos criterios los vemos a continuación.
Criterios de funcionamiento para sintonía en lazo abierto.
Criterio de amortiguamiento 1/4: Combina bien una respuesta rápida junto con un
cierto grado de estabilidad. El amortiguamiento de una respuesta es la relación entre dos rebasamientos
consecutivos. Reacciona bien frente a perturbaciones y es muy utilizado. Los parámetros del regulador se
calculan como se indica en la figura.

Este método fue ideado en 1942 por John G. Ziegler y Nathaniel B. Nichols, si bien su idea original se basaba
en la determinación de los parámetros a partir de la curva de reacción frente a un escalón unitario aplicado a la
entrada (si la entrada no es unitaria habrá que dividir los valores obtenidos en la salida entre el incremento que
se haya aplicado en la entrada). Se necesita representar muchos puntos de la curva y trazar una recta tangente
a la misma en el punto de inflexión.
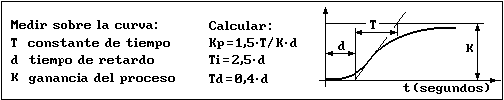
Mínima Integral del Error Absoluto (MIAE): La idea se basa en minimizar la suma de
errores absolutos (sin tener en cuenta el signo), es decir, en hacer mínima el área que se ha rayado en la figura
siguiente. Se consigue una relación de amortiguamiento próxima a 1/4.
Mínima Integral del Cuadrado del Error (MISE): Es equivalente al criterio anterior
puesto que el cuadrado del error siempre es positivo pero penaliza los grandes errores. La respuesta será muy
rápida pero poco amortiguada. Se recomienda para una buena respuesta frente a cambios en carga
(perturbaciones).
Mínima Integral del Error Absoluto multiplicado por el Tiempo (MITAE): La señal
de error multiplicada por el tiempo es similar al error pero más amplificada a medida que el tiempo avanza
(figura siguiente) y por lo tanto serán penalizados los errores tardíos. La respuesta inicial es lenta pero alcanza
pronto el régimen estático. Es adecuado frente a cambios en consigna pero también se adapta a cambios en
carga con un tiempo de respuesta y estabilización aceptables frente a cambios en consigna.

En la figura anterior se muestran los coeficientes y las fórmulas de cálculo de los parámetros del PI y del PID
según los tres últimos criterios. Los coeficientes (a y b) correspondientes al PID solo son válidos si la respuesta
del proceso a una entrada escalón es siempre creciente y el cociente tau/T es menor de 1.
Sintonía de parámetros en lazo cerrado.
Ziegler y Nichols también describieron una técnica de ajuste en lazo cerrado pero con la parte integral y la parte
derivativa anuladas. La constante proporcional (Kp) es incrementada hasta que una perturbación causa una
oscilación mantenida (que no se anula). El valor más pequeño de la constante proporcional que causa tal
oscilación se denomina constante proporcional crítica (Kcrit). El período de esas oscilaciones es el llamado
período de oscilación crítico (Tc). Véase figura.
En el segundo recuadro de la figura tenemos una tabla con las fórmulas de cálculo que se ajustan al criterio
de amortiguamiento 1/4. Es por tanto apropiado cuando deban prevenirse grandes desviaciones frente a
cambios en consigna y en carga y los tiempos de respuesta y estabilización son aceptables al cambiar la
consigna. Este método da resultados precisos pero puede suponer mucho tiempo de prueba y error hasta
conseguir la oscilación mantenida, existiendo además el peligro de inestabilizar el sistema. Se recomienda
generalmente la estimación en lazo abierto (a pesar de ser un método aproximado) porque es más fácil y
porque abarca un mayor número de criterios.

Un método más sencillo, pero solo aproximado, es el método del relé (último recuadro de la figura anterior).
Consiste en sustituir el controlador proporcional por un control todo o nada, que satura o anula la acción de
control sobre el proceso. Aplicando una consigna constante, se utiliza la señal de error para decidir los
momentos de conexión y desconexión (+d y -d en la figura) y cuando la salida alcanza una frecuencia de
oscilación estable, el período coincide aproximadamente con el valor Tc ya explicado. El valor Kcrit se calcula
aproximadamente con la fórmula que tenemos en la figura y finalmente podemos aplicar las mismas fórmulas
de la tabla cental.