 SISTEMA BINARIO.
SISTEMA BINARIO.

 SISTEMA BINARIO.
SISTEMA BINARIO.

Aunque la regla del arrastre se aplica con facilidad, es lógico que no interesa para traducir a otro sistema si el valor es muy grande. Si ha revisado el apartado anterior ya sabrá cómo convertir valores entre cualquier sistema ponderado y el decimal, de modo que nos limitamos a recordarlo:
La base es el número de cifras distintas que utiliza el sistema.
El peso de cada cifra se obtiene de derecha a izquierda comenzando por 1 y
multiplicando por la base para obtener el siguiente.
Paso de un valor a decimal: Se multiplica cada cifra por su peso y se suman los
resultados.
Paso de decimal a otro sistema: Se tantea comenzando por la cifra de mayor
peso, asegurándose de que los pesos acumulados no sobrepasan el valor decimal. Otra forma es dividir
repetidamente el número decimal entre la base del sistema al que deseamos convertirlo y se obtiene el valor
buscado comenzando por el último cociente y los restos en sentido ascendente.
En binario, la base es 2 y los pesos son ...1024 512 256 128 64 32 16 8 4 2 1. Como ocurre en decimal, los ceros a la izquierda no tienen valor, luego los pesos que se aplican están limitados por el número de cifras significativas (sin ceros a la izquierda).
ARITMÉTICA BINARIA.
Las operaciones de sumar, restar, multiplicar y dividir en el sistema binario se hacen de igual forma que en decimal, sin embargo, es normal que la electrónica interna de las máquinas digitales solo tenga capacidad para sumar. Otras operaciones diferentes a la suma se consiguen mediante un conjunto de sumas: La resta de dos valores se consigue sumando a uno de los valores el complemento del otro, es un truco muy ingenioso que veremos en el siguiente apartado. El producto se hace sumando a sí mismo uno de los factores, tantas veces como indique el otro factor. Su eficacia radica en la gran velocidad de cálculo de los procesadores, siendo frecuente además un coprocesador matemático dedicado solo para operaciones, lo que reduce la carga del procesador central. Por último, una división solo es una cuestión de repartir a partes iguales que se puede conseguir por aproximaciones sucesivas. A título informativo se describen a continuación los 4 tipos de operaciones básicas pero como ya se ha indicado, solo presenta interés la suma.
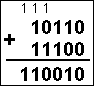
Ejemplo de resta binaria:
Se ha puesto un ejemplo de resta en decimal como punto de referencia para restar en binario. Vea que
empezando por la derecha, en cuarto lugar encontramos que de 7 a 13 van 6 y arrastramos 1 a la izquierda que
se suma al 4 (quedando 5 y faltando 3 para llegar a 8). En sexto lugar encontramos que de 9 a 15 van 6 y
arrastramos 1 a la izquierda que se suma al 9. Esto hace que 9 + 1 = 10, con lo que queda 0 (de 0 a 4 van 4) y
se arrastra el 1 para sumarse al 1 del extremo izquierdo, con lo que de 2 a 5 van 3. En el ejemplo binario, en
cuarto lugar comenzando por la derecha, encontraremos que de 1 a 10 (será 2 pasado a decimal) va 1 y se
arrastra 1 a la izquierda para sumar al 0. En sexto lugar volvemos a encontrar que de 1 a 10 va 1 y se arrastra
1 a la izquierda para sumar al 1 (esto desencadena otro arrastre hasta la última posición izquierda).

Ejemplo de producto binario:
La multiplicación es tan sencilla que no se necesita explicación. Si sabemos multiplicar en sistema
decimal no encontraremos ningún problema para hacerlo en binario. Si el número de cifras es grande, es
posible que se junten muchos unos en las sumas finales, por ejemplo 5 unos cuya suma binaria es 101, en cuyo
caso queda 1, se arrastra un 0 a la izquierda (que no afecta) y se arrastra un 1 dos lugares a la izquierda.

Ejemplo de división binaria:
En este ejemplo, hay que comenzar cogiendo 4 cifras del dividendo para sobrepasar al divisor. Así
resulta que 1011 entre 111 toca a 1 (solo puede ser 1 o 0). 1 por 111 es 111 y falta 100 hasta llegar a 1011.
Bajando la siguiente cifra (un 0) resulta que 1000 entre 111 toca a 1. Así sucesivamente.
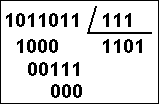
El problema que se trata de resolver es la forma de expresar números negativos en el sistema binario, valiéndonos únicamente de señales que solo pueden ser verdaderas o falsas. Es cierto que una de las señales podría representar el signo y el resto de las cifras formarían siempre un valor positivo, pero la electrónica del dispositivo sería compleja porque debería ser capaz de restar cuando encontrara el signo menos.
Parece imposible, pero los complementos permiten hacer restas mediante sumas y reducen con ello la electrónica de la máquina. ¿Cree por ejemplo que el valor 9279 es igual a -721? Si los valores (en este ejemplo) se manipulan siempre en registros de 4 cifras y todo lo que se salga desaparece, entonces es cierto y lo vamos a ver: Si hacemos la suma 721 + 9279 se obtiene el valor 10000, pero como se ha dicho, en un registro de 4 cifras solo caben los 4 ceros y el 1 se pierde. Si en el registro solo hay ceros, el resultado hay que considerarlo 0, por lo tanto 721 + 9279 = 0, lo que solo es posible si 9279 es igual a -721.
Por supuesto, se puede pensar que se trata de un truco, y lo es, pero esto es lo que funciona realmente en los dispositivos digitales: Cuando introducimos dos valores y los restamos, la máquina transforma uno de los datos de manera que resuelve la resta haciendo una suma. Las reglas de la transformación tienen que ser muy simples ya que de lo contrario no compensaría el esfuerzo y tratándose del sistema binario, realmente son muy sencillas.
El complemento a 1 de un valor binario se obtiene invirtiendo el estado de todas sus cifras, incluyendo los ceros a la izquierda hasta completar la capacidad del registro. Por ejemplo, el valor 10011 en un registro de 8 bits (cifras) será 00010011 y su complemento a 1 será 11101100.
El complemento a 2 de un valor binario se obtiene sumando 1 al complemento a 1. Por ejemplo, el complemento a 2 de 10011 (el mismo anterior) será 11101100 + 1 = 11101101.
Cómo restar sumando: El complemento a 2 de un número binario se puede considerar directamente su equivalente negativo. Por lo tanto, para hacer la resta a - b = ¿x? basta con calcular el resultado "x" (sin olvidar el tamaño del registro que se utilice) como:
El tamaño de los registros es normalmente el número de bits del procesador de la máquina, actualmente 32 en la mayoría de los ordenadores y autómatas industriales. Otra forma de restar sumando consiste en utilizar el complemento a 1, pero en este caso, el 1 de arrastre que se sale fuera del registro se suma de nuevo al resultado, quedando en el registro el resultado esperado de la resta.
Bit de signo: Suponiendo que un registro es de 4 bits, ¿qué podemos pensar de un valor como 1101? ¿será positivo o negativo? No hay duda: Cuando el bit de mayor peso (el que está más a la izquierda en el registro que contiene al número) sea un uno significa que es negativo y si es un cero será positivo. Esto es así porque al complementar un valor (al hacerlo negativo), los ceros a la izquierda también se transforman en unos, incluido el bit de mayor peso. Como el complemento a 2 de 1101 es 0011, entonces resulta que 1101 = -0011 = -310.
La conclusión anterior afecta directamente a la programación de cualquier dispositivo programable, así por ejemplo cuando se define un dato como entero con signo en un procesador de 32 bits, el número positivo más grande será un cero seguido de 31 unos, que equivale en decimal a 231 - 1. Igualmente, el valor negativo más bajo será un uno seguido de 31 ceros, que equivale en decimal a -(231). Por el contrario, cuando un dato se define como entero sin signo, el contenido siempre será positivo, siendo el valor más bajo el cero y el más grande será 232 - 1, es decir, 32 unos. En programación, cada tipo de dato tiene asignado un determinado número de bits, otros ejemplos pueden ser los enteros largos y los reales o dobles, a los que se destina normalmente el doble de bits que al entero. Lo importante es que debe tenerse una cierta precaución en las operaciones, ya que si el resultado desborda la capacidad del registro podemos encontrarnos con la sorpresa de que nos devuelve un valor extraño que además puede estar cambiado de signo.
NÚMEROS REALES (coma flotante).
Números como 10, 45 o -13 son valores enteros que se manipulan con las operaciones que ya conocemos. Otra cosa son los valores como 25,47 que no son enteros pero al igual que los anteriores forman parte del conjunto de los números reales. En binario también tienen representación los números con decimales: Cada cifra que haya después de la coma tiene igualmente un peso que depende de su posición, comienza por la izquierda con valor igual a 1/2 y decrece hacia la derecha, siempre multiplicando por 1/2 para obtener el siguiente. Veamos un ejemplo:
Para pasar de decimal a binario se pasa normalmente la parte entera y la parte decimal se va multiplicando por 2 hasta que se anulan los decimales y los decimales binarios se obtienen con la parte entera que se obtiene en cada paso. Por ejemplo:
0,375·2 = 0,750 (primer decimal el 0); 0,75·2 = 1,50 (segundo decimal el 1); 0,50·2 = 1,0 (tercer decimal el 1).
Queda finalmente: 25,37510 = 11001,0112
La forma anterior de proceder es complicada de implementar con electrónica digital o al menos existe otra manera mucho más sencilla que es la coma flotante. Sin coma flotante, es necesario seguir la pista a la posición de la coma cada vez que se hace una operación y al operar con los valores de dos registros no puede relacionarse directamente bit con bit de iguales posiciones, ya que al variar las posiciones de las comas hacen que los pesos de cada bit también se desplacen.
En coma flotante cada número se expresa con un valor entero y un exponente de la base del sistema, por ejemplo, el valor -43,425 será igual a -43425·10-3 (notación científica), es decir, queda definido por el valor entero -43425 y el exponente -3. En los registros, se destina un número fijo de cifras para el valor entero y el resto de cifras para el exponente. Al multiplicar los valores de dos registros, simplemente se multiplican los enteros y se suman los exponentes. Al dividir, se dividen los enteros y se restan los exponentes. Para sumar o restar dos valores, se suman o restan los enteros y se mantienen los exponentes, siempre y cuando tengan igual exponente. Por ejemplo, no se puede sumar directamente 103·10-2 con 235·10-1, pero sí se puede sumar 103·10-2 con 2350·10-2 porque ya tienen igual exponente y el resultado será (103 + 2350)·10-2. Nótese que al restar un valor al exponente, hay que multiplicar al entero por la base (10 en sistema decimal, 2 en binario) elevada al valor que se resta al exponente. Los valores límite en este tipo de representación dependen por separado del número de bits asignados al entero y al exponente.