Valuación de Acciones
![]()
Para ilustrar el proceso de valuación de las acciones comunes, Campbell y Morris le solicitaron que analice la empresa Bon Temps Company, una agencia de empleos que proporciona operadores de procesadores de textos y programadores de computadoras a aquellas compañías que tienen cargas de trabajo temporales excesivas. Usted deberá responder las siguientes preguntas:
a) 1) Escriba una formula que pueda utilizarse para valuar cualquier acción, independientemente de su patrón de dividendos.
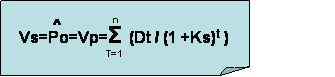
Donde Dt son los dividendos que el accionista espera recibir al final del año, y Ks es la tasa requerida de rendimiento, o tasa mínima aceptable sobre una acción.
2) ¿Qué es una acción con un crecimiento constante?.
Son acciones que experimentan creciemiento en las utilidades y dividendos cada año.
¿Cómo se valúan este tipo de acciones?
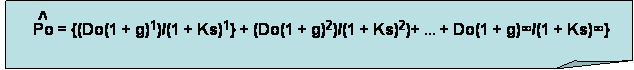
3) ¿Qué sucederá si el crecimiento es constante, y g > ks?. ¿Habrá muchas acciones en las que g > ks?
Si g > ks la acción generará dividendos.
b) Suponga que Bon Temps tiene un coeficiente beta de 1.2; que la tasa libre de riesgo (el rendimiento de los bonos de la tesorería) es de 10%, y que la tasa requerida de rendimiento sobre el mercado es de 15%. ¿Cuál es la tasa requerida de rendimiento sobre las acciones de la empresa?.
Utilizando la siguiente ecuación:
![]()
Donde bs = 1.2; KRF = 10% y Km = 15%, Obtenemos como resultado que la tasa requerida de rendimiento es de Ks= 16%
c) Suponga que Bon Temps es una compañía con un crecimiento constante, cuyo último dividendo (Do, el cual se pago el día de ayer) fue de dos dólares y cuyos dividendos se espera que crezcan indefinidamente a una tasa de 6%.
1) ¿Cuál será la corriente esperada de dividendos de la empresa a lo largo de los tres años siguientes?
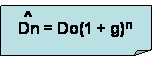
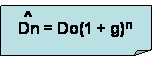 Utilizando
la ecuación:
Utilizando
la ecuación:
Donde Do=$2; g=0,06; n=3; tenemos que la corriente esperada de dividendos es de $2,38.
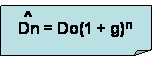
2) ¿Cuál es el precio actual de las acciones de la empresa?.
Utilizando la ecuación:
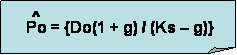
Donde Do=$2; g=0,06; Ks=0,16. Nos queda que el precio actual de las acciones es de $21,2.
3) ¿Cuál, el valor esperado de las acciones dentro de un año?
Utilizando la siguiente ecuación:
Donde Do=$2; g=0,06; tenemos como resultado Dn=2,2472.
Utilizando la siguiente ecuación:
Donde Dn=2,2472; Ks=0,16; g=0,06. Tenemos que Pn= $22,47
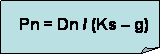
4) ¿Cuáles, los rendimientos esperados por dividendos, por ganancias de capital y total durante el primer año?.
Ganancia de Capital = Precio final - Precio inicial= $(22,47 - 21,20) = $ 1,27
Rendimientos por Ganancia de Capital = Ganancia capital / Precio inicial = $ (1,27 / 21,2) = 0,0599= 6%
![]()
![]() Rendimiento por Dividendos =
D2 / P1 = $ (2,2472 / 22,47 ) =
0,10
= 10%
Rendimiento por Dividendos =
D2 / P1 = $ (2,2472 / 22,47 ) =
0,10
= 10%
Rendimiento Total = 16%
d) Ahora, suponga que las acciones se venden actualmente a 21,20 dólares. ¿Cuál será la tasa esperada de rendimiento de las acciones?
Utilizando la siguiente ecuación:

Tenemos que D1= 2,12; Po= 21,20; g=0,06. Por lo tanto Ks= 0,16 = 16%.
e) ¿Cuál sería el precio de las acciones si se espera que sus dividendos tengan un crecimiento cero?
Tenemos que Po = D / Ks = $ 2 / 0,16 = $ 12,50
f) Ahora, suponga que se espera que las utilidades y los dividendos de Bon Temps experimente un crecimiento supernormal de 30% a lo largo de los tres años siguientes, y posteriormente regrese a su tasa constante de crecimiento a largo plazo de 6%. ¿Cuál será el valor de sus acciones bajo estas condiciones?. ¿Cuáles serán los rendimientos esperados por dividendos y por ganancias de capital en el año 1?, ¿Y en el año 4?.
Por medio de la ecuación:
Calculamos los dividendos de cada año durante el periodo de crecimiento inconstante:
Para Do= $2; g=0,3; n=1. D1= $2,6.
Para Do= $2; g=0,3; n=2. D2= $3,38.
Para Do= $2; g=0,3; n=3. D3= $4,394.
El valor presente de las acciones es el valor presente de los dividendos desde el año 1 hasta el infinito. Por lo tanto en teoría, se puede continuar calculando cada dividendo futuro mas allá del año 3, cuando ocurre el crecimiento normal de 6%.
Para Do= $4,394; g=0,06; n=1. D4= $4,6576
Para Do= $4,394; g=0,06; n=2. D5= $4,9371
Para Do= $4,394; g=0,06; n=3. D6= $5,2333
Para Do= $4,394; g=0,06; n=17. D20= $11,8320
Se puede continuar hasta encontrar el VP de la corriente de dividendos. Pero ya que después que se haya pagado D3 en el año 3, la acción quedará sujeta a un crecimiento constante, se puede aplicar la fórmula de crecimiento constante en ese punto y determinar el valor de P3, el cual es el vaor presente de los dividendos desde el año 4 hasta el infinito como se evaluó en el año 3. Después de que se paga el dividendo del año 3, todos los dividendos a futuro crecerán a una tasa constante. Por lo tanto:
P3 = D4 / (Ks – gn); sustituyendo tenemos: P3 = { $ 4,6576 / (0,16 – 0,06)} = $ 46,58
Flujo de efectivo total que reconocemos en el año 3 es la suma de D3 + P3 = $ 4,394 + $ 46,58 = $ 50.97
Luego procedemos al cálculo del valor presente para cada flujo:
![]()
![]()
![]()
![]()
Pn= Dn/(1+i)n
Para D1= 2,6; i=0,16; n=1. P1= $2,24
Para D2= 3,38; i=0,16; n=2. P2= $2,51
Para D3= 50,97; i=0,16; n=3. P3= $32,656
Pototal = $ (2,24 + 2,51 + 32,656) = $ 37,41
Se ha calculado que el valor de la acción de crecimiento sp normal es de $37,41.
g) Suponga que se espera que Bon Temps experimente un crecimiento de cero durante los tres primeros años y posteriormente retome su crecimiento uniforme de 6% en el cuarto año. ¿Cuál será el valor de las acciones el día de hoy?. ¿Cuáles, los rendimientos esperados por dividendos y por ganancias de capital en el año 1?, ¿Yen el año 4?.
Po = $ 2 / (1 + 0.16)1 + $ 2 / (1.16)2 + $ 2 / (1.16)3 => Po = $ 4.4917
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D4 = $ 2(1.06)1 = $ 2.12
D5 = $ 2(1.06)2 = $ 2.25
P4 = $ 2.25 / (0.16 – 0.06) = $ 22.50 ;
Flujo de efectivo total al año 4: $ 22.50 + $ 2.12 = $ 24.62
Po4 = $ 24.62 / (1.16)4 = $ 13.60
Pototal = $ 4.4917 + $ 13.60 = $ 18.10
h) Finalmente, suponga que se espera que las utilidades y los dividendos de Bon Temps disminuyan a una tasa constante de 6% por año, es decir, g = -6%. ¿Por qué alguien podría comprar una de tales acciones, y a que precio debería venderla?¿Cuáles serian los rendimientos por dividendos y por ganancias de capital de cada año?.
Tomando como datos g = - 6% ; Do = 2 tenemos:
D1 = 2(1 + (-0.06))1= $ 1.88
D2 = 2(1 + (-0.06))2 = $ 1.77
D3 = 2 (1 + (-0.06))3 = $ 1.66
Po = {2(1 + (-0.06)) / (0.16 – 0.06)} = $ 8.54
Sección III: Valuación de Activos Reales.
La empresa Mutual Chicago examina la posibilidad de comprar una cierta pieza de equipo que explorara datos dentro de su computadora principal. El nuevo explorador eliminará la necesidad de contratar ayuda de tiempo parcial para asegurarse de que la información sobre los clientes se registre en forma exacta y oportuna. Después de evaluar todos los beneficios y costos futuros, la administración ha determinado que el nuevo explorador generará los siguientes flujos de efectivo durante sus diez años de vida:
|
Año / periodo |
Flujo de Efectivo Esperado, FEt |
|
1 – 3 |
$30000 |
|
4 – 6 |
15000 |
|
7 |
-20000 |
|
8 – 10 |
10000 |
A Campbell y Morris les gustaría que usted evaluara el valor del explorador.
a) Si Mutual y Chicago consideran que el rendimiento apropiado de las inversiones como el explorador es de 15%, ¿Cuál será el valor del explorador para la compañía?.
Vo = $ 1000[30(1.15)1 + 30(1.15)2 + 30(1.15)3 + 15(1.15)4 + 15(1.15)5 + 15(1.15)6 - 20(1.15)7+ 10(1.15)8+10(1.15)9+ 10(1.15)10 ]
Vo = $ 92080
b) ¿Recomendaría usted que se comprara la maquina, si su costo actual fuera de 100000 dólares?. Explique su razonamiento.
No se recomienda realizar la compra del activo.
c) ¿Sería más atractivo el explorador, si el rendimiento apropiado fuera de 10%, en lugar de 15%?. Explique su respuesta
Vo = $ 1000[30(1.10)1 + 30(1.10)2 + 30(1.10)3 + 15(1.10)4 + 15(1.10)5 + 15(1.10)6 - 20(1.10)7+ 10(1.10)8+10(1.10)9+ 10(1.10)10 ]
Vo = $ 105140
![]()