PROBLEMA DE INTEGRACION CAPITULO 6 - BESLEY
![]()
6-31 Realice las siguientes tareas.
a) Dibuje líneas de tiempo de flujo de efectivo de:
1) Un flujo de efectivo por una suma acumulada de 100 dólares al final del año 2.
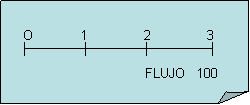
2) Una anualidad ordinaria de cién dolares por año durante tres años.
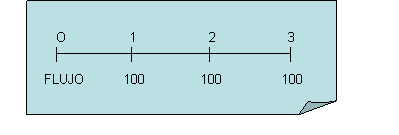
3) Una corriente desigual de flujo de efectivo de -50, 100, 75 y 50 dólares al final de los años 0 a 3.
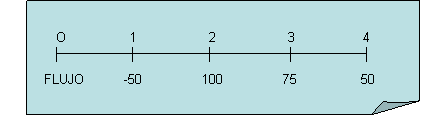
b) 1) ¿Cuál será el valor futuro de una suma inicial de cien dólares después de 3 años si éstas se invierten en una cuenta que paga 10% anual de interés?
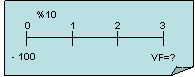 Por medio del siguiente análisis del flujo de efectivo:
Por medio del siguiente análisis del flujo de efectivo:
![]()

Utilizando la siguiente ecuación:
donde VP= $100; i=0,10 y n= 3, obtenemos que el valor futuro de $100 después de 3 años es de $133,10.
2) ¿Cuál será el valor presente de cien dólares que se vayan a recibir dentro de tres años, si la tasa de interés apropiada es de 10 por ciento?
 Por medio del siguiente análisis del flujo de efectivo:
Por medio del siguiente análisis del flujo de efectivo: 

Utilizando la siguiente ecuación:
donde VF= $100 ; i= 0,10 y n= 3, obtenemos que el valor presente de estos $100 es de $75,13.
c) Algunas veces necesitamos determinar el tiempo que se requiere para que una suma de dinero (o cualquier otra cosa) crezca hasta alcanzar una cantidad específica. Por ejemplo, si las ventas de una compañia están creciendo a una tasa de 20% anual, ¿Cuánto tiempo se necesitará para que las ventas se tripliquen?
Realizando el siguiente análisis de flujo de efectivo: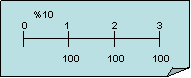
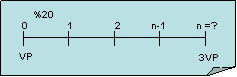
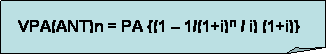
Y utilizando la siguiente ecuación:
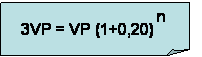
Podemos sustituir los valores y obtenemos:
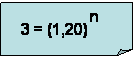
despejando:
aplicando Ln a ambos lados de la ecuación:
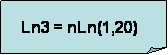
Por lo tanto las ventas se triplicaran a los seis periodos (n= 6).

d) ¿Cuál es la diferencia que existe entre una anualidad ordinaria y una anticipada? ¿ Qué tipo de anualidad es la que se muestra en la siguiente línea de tiempo de flujo de efectivo? ¿ Cómo la cambiaría usted al otro tipo de anualidad?

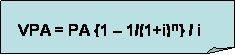
En la anualidad ordinaria los pagos ocurren el final de cada periodo, y con la anticipada los pagos ocurren al inicio de cada periodo. El grafico de la linea de tiempo de flujo de efectivo anterior muestra una anualidad ordinaria. Para expresar el grafico anterior a la forma de anualidad anticipada se realizaría de la siguiente forma:
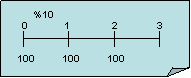
e) 1) ¿Cuál será el valor futuro de una anualidad ordinaria a tres años de cien dólares, si la tasa de interés apropiada es de 10 por ciento?
El flujo de efectivo de la anualidad se muestra de la siguiente forma:
Utilizando la siguiente ecuación:
Donde PA= 100, i=0,10 y n=3. Obtenemos que el valor futuro es de $331.
![]()
2) ¿Cuál es el valor presente de la anualidad?
Por medio de la siguiente ecuación:
Donde PA=100; n=3; i= 0,10. Obtenemos que el Valor presente de la anualidad es de $248,68.

3) ¿Cuales serían los valores presentes y los valores futuros si la anualidad fuera una anualidad anticipada?
Para calcular el valor presente utilizamos la siguiente ecuación:
Donde PA=100; n=3 ; i=0,10. Obtenemos como resultado VPA= $273,55
Para calcular el valor futuro utilizamos la siguiente ecuación:
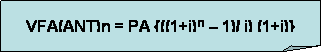
Donde PA= 100; i=0,10; y n=3. Obtenemos como resultado VFA= $364,10
f) ¿Cuál será el valor presente de la siguiente corriente desigual de flujos de efectivo? La tasa de interés apropiada es de 10%, anualmente compuesta.

Utilizando la siguiente ecuación podemos traer a valor presente cada uno de los flujos de efectivo en cada período para despues realizar la sumatoria de los mismos.

Por lo tanto para
n=1; VF= 100; n=1; i=0,10. VP1= $90,91
n=2; VF= 300; n=2; i=0,10. VP2= $247,93
n=3; VF= 300; n=3; i=0,10. VP3= $225,56
n=4; VF= -50; n=4; i=0,10. VP4= $-34,25
Realizada la sumatoria nos queda que el VP= $530,15.
g) ¿Qué tasa anual de interés ocasionará que cien dólares crezcan hasta 125,97 dólares dentro de tres años?
La gráfica del flujo de efectivo se muestra de la siguiente forma:

Utlizamos la siguiente ecuación:
Donde VFn= 125,97; VP=100; i=0,10; n=3. Despejando nos queda que i= 8%
h) 1) ¿Será el valor futuro mayor o menor si capitalizamos un monto inicial con una frecuencia mayor a la de un año, por ejemplo, cada seis meses, o semestralmente, manteniendo constante la tasa de interés cotizada?
El valor futuro será mayor ya que se está capitalizando con una frecuencia mayor, ganando intereses sobre el capital y sobre los intereses de cada periodo.
2) Defina tasa de interés simple estipulada o cotizada, tasa periódica y tasa anual efectiva (TAE).
Tasa de interés simple estipulada o cotizada: Es la tasa cotizada por los prestamistas y los prestatarios utlizada para determinar la tasa ganada durante cada período de capitalización.
Tasa periódica:Tasa cargada por un prestamista o pagada por un prestatario, cada período de intereses (por ejemplo: mensual, trimestral, anual y así en forma sucesiva).
Tasa anual efectiva (TAE): Tasa anual que se gana o se paga considerando una capitalización de intereses durante el año (esto es, tasa anual equivalente a una tasa períodica que se capitaliza a lo largo de m periodos durante el año).
3) ¿Cuál es la TAE correspondiente a una tasa de interés simple de 10% semestralmente compuesta? ¿Trimestralmente compuesta? ¿Diariamente compuesta?
Utilizando la siguiente ecuación:
Para una tasa semestralmente compuesta, tenemos que isimple= 0,10; m=2. Obteniendo como resultado TAE= 10,25%
Para una tasa trimestalmente compuesta, tenemos que isimple= 0,10; m=4. Tenemos como resultado TAE= 10,38%
Finalmente una tasa diariemente compuesta, tenemos que isimple= 0,10; m=365. Obtenemos como resultado TAE= 10,52%
4) ¿Cuál será el valor futuro de cien dólares después de tres años, bajo una capitalización semestral de 10%? ¿Y bajo una capitalización trimestral?
Utilizando la siguiente ecuación:
Tenemos que para una capitalización semestral m=2; VP=$100; i= 0,10; n=3; . Obtenemos que el VF=$134.
Para una capitalización trimestral m=4; VP=$100; i=0,10; n=3; Obtenemos que el VF= $134,38
i) ¿Alguna vez la tasa efectiva anual será igual a la tasa de interés simple (cotizada)? Explique su respuesta.
Si puede ser igual si se aplica una capitalización anual.
j) 1) ¿Cuál será el valor de la siguiente corriente de flujo de efectivo al final del año 3, si la tasa de interés cotizada es de 10%, semestralmente compuesta?
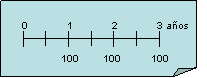

![]()
Tenemos la siguiente ecuación
donde isimple es 0,10 y m=2. Por lo que obtenemos una Tasa periódica de i=0,05.
Y por medio de la ecuación
Donde PA=100; i= 0,05; n= 6, tenemos como resultado VFA = $ 680.19
2) ¿Cuál será el valor presente de la misma corriente?
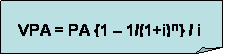
Para buscar el valor presente utilizamos la ecuación:
Donde PA=$100; i=0,05; n=6. Obtenemos que VPA= $507.57
3) ¿Será la corriente de efectivo una anualidad?
Si en este caso tenemos que la corriente de efectivo se comporta como una anualidad.
4) Una regla importante es que usted no debería nunca mostrar una tasa de interés simple sobre una línea de tiempo o utilizarla en los cálculos, a menos de que se mantengan ciertas condiciones. ¿Cuáles son estas condiciones? (Indicación de importancia: piense en una capitalización anual, cuando isimple=TAE) Qué estaria mal respecto a sus respuestas a las preguntas j1) y j2) si usted aplicara la tasa de interés simple de 10% en lugar de la tasa de interés períodica isimple/2=10%/2= 5 por ciento?
La condición es que la capitalización ocurra sólo una vez al año, cuando isimple = tasa periódica = TAE. Si se usara un interés simple de 10% los valores presentes y futuros variarían porque su capitalización sería diferente.
k) 1) Elabore un programa de amortización para un préstamo de 1000 dólares cotizado a una tasa anual de 10% sujeto a tres pagos iguales.
Utilizando siguiente ecuación:
Donde PA=$1000; n=3; i= 0,10. Obtenemos un PA= 402,17. Para luego proceder a llenar el siguiente cuadro:
| Año | Monto Inicial (1) | Pago (2) | Interés (3) | Reembolso del Capital (2)-(3) | Saldo (5) |
| 1 | $1000 | $402,17 | $100 | $302,17 | $697,83 |
| 2 | $697,83 | $402,17 | $70 | $332,17 | $365,66 |
| 3 | $365,66 | $402,17 | $36,57 | $365,6 | 0 |
2) ¿Cuál será el gasto anual de intereses para el prestatario y el ingreso anual por intereses por el prestamista durante el año 2?
Este es de $70.
![]()