CAPITULO 8 – TECNICAS DEL PRESUPUESTO
DE CAPITAL
Problema de integración
Su jefe, el
director financiero de Southern Textiles (CFO) acaba de proporcionarle los
flujos de efectivo estimados de dos proyectos
propuestos. El proyecto L implica añadir un nuevo articulo a la línea
textil de la empresa; se requerirá de algún tiempo para edificar el mercado
para este producto, por lo que los
flujos de entrada de efectivo aumentarían a través del tiempo. El proyecto C
implica hacer una adición a la línea existente, y su flujo de efectivo
disminuirán con el transcurso del tiempo. Ambos proyectos tienen vida de tres
años, por que Southern plantea introducir una tela
totalmente nueva en ese momento.
A continuación se presentan las estimaciones de flujo de efectivo (en
millares de dólares):
Flujos Netos de Efectivos Esperados
|
Año |
Proyecto L
|
Proyecto C
|
|
0 |
$ (100) |
$ (100) |
|
1 |
10 |
70 |
|
2 |
60 |
50 |
|
3 |
80 |
20 |
La depreciación, los valores de recuperación los efectos fiscales y
otros conceptos similares se encuentran incluidos en estos flujos de efectivo.
El director financiero evaluó subjetivamente el riesgo de cada proyecto,
y ha incluido que ambos tienen características de riesgo similares al promedio
de los proyectos de la empresa.
La tasa requerida de rendimiento de Southwestern es del 10 %. Usted debe
de determinar si uno de los proyectos o los dos deberían aceptarse.
Empiece su análisis respondiendo las siguientes preguntas:
a) ¿Qué
es el presupuesto de Capital? ¿Existen similitudes entre las decisiones de
presupuesto de capital de una empresa y las decisiones de inversión de un
individuo?
Es el proceso que se sigue para planear y evaluar los
gastos erogados sobre aquellos activos cuyos flujos de efectivo se espera que
se extiendan más allá de un año. Si existen similitudes entre las decisiones de
presupuesto de capital de una empresa y las decisiones de inversión de un
individuo, ya que este es el proceso mediante el cual la empresa evalúa los
proyectos y decide cuales son las inversiones aceptables y las que deberían ser adoptadas.
b) ¿Cuál
es la diferencia que existe entre los proyectos independientes y los proyectos
mutuamente excluyentes?
Los proyectos independientes son aquellos cuyos
flujos de efectivo no se afectan entre sí, por lo que la aceptación de uno de
ellos no condiciona la aceptación de cualquiera de los otros; es decir, todos
los proyectos independientes pueden ser puestos en práctica si son aceptables.
En cambio en los proyectos mutuamente excluyentes, cuando se adopta uno de
ellos los demás deben ser rechazados, es decir sólo se puede adoptar un
proyecto mutuamente excluyente, aun si todos ellos son aceptables.
¿Cuál,
es la diferencia que existe entre los proyectos que tienen flujos de efectivo
convencionales y aquellos que tienen flujo de efectivo no convencionales?
Un proyecto tiene un de flujo de efectivo
convencional si tiene flujos de salida de efectivo en uno o más periodos al
inicio de su vida, seguidos por una serie de flujos de entrada, y un proyecto
tiene un flujo de efectivo no convencional al presentar flujos de salida de
efectivo, en cualquier momento durante su vida o al final de la misma.
c) 1) ¿Qué es el periodo de recuperación?
El periodo de recuperación es el plazo que transcurre antes de que se
recupere el costo original de una inversión a partir de los flujos de efectivo
esperados.
Determine
los periodos de recuperación
tradicionales de los proyectos L y C.
PROYECTO
L.
PROYECTO
C.
Utilizando la siguiente ecuación:
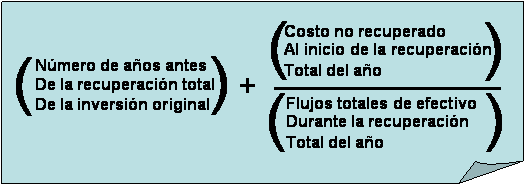
Tenemos
para el proyecto L
Número de años antes de la recuperación total de la
inversión original: 2
Costo no recuperado al inicio de la recuperación
total del año: 30
Flujos totales de efectivo durante la recuperación
total del año: 80
El
resultado es de 2,375 años.
Para
el proyecto C
Número de años antes de la recuperación total de la
inversión original: 1
Costo no recuperado al inicio de la recuperación
total del año: 30
Flujos totales de efectivo durante la recuperación
total del año: 50
El
período de recuperación es de 1,6 años.
2) ¿Cuál
es el fundamento en el cual se apoya la medida del periodo de recuperación?
Para calcular el período de recuperación de un
proyecto, se deben añadir los flujos de efectivo esperados de cada año hasta
que se recupere el monto inicialmente invertido en el proyecto. La cantidad
total de tiempo incluyendo una fracción de un año en caso de que ello sea
apropiado, que se requiere para recobrar la cantidad original invertida es el
periodo de recuperación. Como regla general un proyecto se considera aceptable
si su período de recuperación es inferior al plazo máximo de recuperación de
costos establecido por la empresa.
De
acuerdo con el criterio del periodo de recuperación, ¿qué proyecto o proyectos
deberían aceptarse, si el periodo máximo de recuperación de la empresa es de
dos años y los proyectos L y C son independientes?
Se debería aceptar el proyecto
C, ya que está dentro del período de recuperación de la empresa.
¿Y
si fueron mutuamente excluyentes?
Se debería aceptar solo el proyecto C
3) ¿Cuál es la diferencia que existe entre el
periodo de recuperación tradicional y el descontado?
A diferencia del cálculo del período de recuperación
tradicional, el de recuperación descontado considera el valor del dinero a
través del tiempo, cuando se utiliza este método el proyecto debería ser
aceptado cuando su período de recuperación descontado sea inferior a su vida
esperada.
El método del período de recuperación tradicional
pasa por alto el valor del dinero a través del tiempo, por lo que la
dependencia exclusiva de este método puede conducir a la toma de decisiones
incorrectas, por medio de la técnica del período de recuperación descontado, se
pueden evaluar las propuestas de inversión que emplean conceptos del valor del
dinero a través del tiempo; estas son el valor presente neto (VPN) y la tasa
interna de rendimiento (TIR).
4) ¿Cuales son las principales desventajas del
periodo de recuperación tradicional?
·
Pasa por
alto el valor del dinero a través del tiempo
·
Se
conoce la rapidez con la cual la inversión inicial quedará cubierta por los
flujos de efectivo esperados, pero esta información no nos indica si el
rendimiento sobre el proyecto será suficiente para cubrir el costo de los
fondos invertidos.
·
Cuando
se utiliza este método, los flujos de efectivo que superan dicho periodo son
ignorados.
¿Es este método de alguna utilidad real en las decisiones de presupuesto
de capital?
Este método ha sido tradicionalmente una de las
técnicas de presupuesto de capital más populares, sin embargo si se depende
exclusivamente de él puede conducir a la toma de decisiones incorrectas, si la
meta fuese la maximización del valor de la empresa.
d) 1) Defina valor presente neto (VPN).
Es el método utilizado para evaluar las propuestas de
las inversiones de capital, mediante la determinación del valor presente de los
flujos netos futuros de efectivo, descontados a la tasa de rendimiento
requerida por la empresa.
¿Cuál es el VPN de cada proyecto?
Proyecto L.
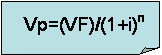Mediante la siguiente ecuación:
Tenemos
que:
Para n=0;
VF=-100; i=0,10. El resultado es VP= -100
Para n=1;
VF= 10; i=0,10. El resultado es VP= 9,090
Para n=2; VF=
60; i=0,10. El resultado es VP= 49,5868
Para n=3;
VF=80; i=0,10. El resultado es VP= 60,1052
La
sumatoria de todos los flujos nos dice que el VPN para el Proyecto L es de $18,782 millares.
Proyecto C.
Tenemos
que:
Para n=0;
VF=-100; i=0,10. El resultado es VP= -100
Para n=1;
VF= 70; i=0,10. El resultado es VP= 63,6364
Para n=2;
VF= 50; i=0,10. El resultado es VP= 41,3223
Para n=3;
VF= 20; i=0,10. El resultado es VP=
15,0263
La
sumatoria de todos los flujos nos dice que el VPN para el Proyecto C es de $19,985 millares.
2) ¿Cuál
es el fundamento en el que se basa el método del VPN?
Este método se basa en las técnicas del flujo de
efectivo descontado, para aplicar este enfoque se debe determinar el valor
presente de todos los flujos futuros de efectivo que se espera que genere un
proyecto, y luego sustraer la inversión original para precisar el beneficio
neto que la empresa obtendrá del hecho de invertir en el proyecto. Si el
beneficio neto que se ha calculado sobre la base de un valor presente es
positivo, el proyecto se considera una inversión aceptable.
De acuerdo
con el mismo, ¿qué proyecto o proyectos deberían aceptarse si todo ellos fueran
independientes? ¿Y si fueran mutuamente excluyentes?
De
acuerdo al criterio de VPN se debería tomar el Proyecto C
3)
¿cambiarían los VPN si cambiaran la tasa de rendimiento requerida?
Los
VPN cambiarían si cambia la tasa de rendimiento ya que ella influye
directamente en el cálculo de los mismos.
d) 1.-Defina
él termino tasa interna de rendimiento
(TIR).
Es la tasa de descuento que obliga al valor presente
de los flujos de efectivo esperados de un proyecto a igualar su costo inicial,
esta es similar al rendimiento al vencimiento de un bono.
¿Cuál es la TIR de cada proyecto?
Proyecto
L
Planteamos la ecuación de la siguiente manera:
(-$100)
+ (10)/(1+TIR)1 + (60)/(1+TIR)2 + (80)/(1+TIR)3
= 0
Mediante tanteo tenemos como resultado una TIR= 18% para el Proyecto L.
Proyecto
C
Para el proyecto C volvemos a plantear la ecuación:
(-$100)
+ (70)/(1+TIR)1 + (50)/(1+TIR)2
+ (20)/(1+TIR)3 = 0
El resultado del tanteo es una TIR= 23,5% para el Proyecto C.
2.-
¿Cómo se relaciona la TIR de un proyecto con el rendimiento al vencimiento de
un bono?
Si se invierte en un bono y se mantiene hasta su
vencimiento se podrá obtener el rendimiento al vencimiento (RAV), o la tasa de
rendimiento del bono sobre el dinero que se haya invertido, de manera análoga
se emplean exactamente los mismos conceptos cuando se utiliza el método de la
tasa interna de rendimiento, es decir, la tasa que la empresa espera obtener
sise decide llevar a cabo el proyecto.
3.-
¿Cuál es la lógica en la que se basa el método de la TIR? De acuerdo con la
TIR, ¿qué proyectos deberían llevarse a cabo si fueran independientes? ¿Y si
fuera mutuamente excluyente?
El aceptar un proyecto cuya TIR supera su tasa de
rendimiento
4.- ¿Cambiarían las TIR de los
proyectos si cambiara la tasa requerida de rendimiento? Explique su respuesta.
F)
1)
Dibuje los perfiles de VPN de los proyectos L y C. ¿A qué tasas de
descuentos se cruzan estos perfiles?
Proyecto
L
(-$100)
+ (10)/(1+TIR)1 + (60)/(1+TIR)2 + (80)/(1+TIR)3
= VPL
Proyecto
C
(-$100)
+ (70)/(1+TIR)1 + (50)/(1+TIR)2
+ (20)/(1+TIR)3 = VPc
Con
las ecuaciones anteriores procedemos a elaborar un cuadro según las diferentes
Tasas de Descuento.
|
Tasa
de Descuento (%) |
VPN
– L ($) |
VPN
– C ($) |
|
0 |
50 |
40 |
|
5 |
33,05 |
29,29 |
|
10 |
18,78 |
20 |
|
15 |
6,67 |
11,83 |
|
20 |
-3,70 |
4,63 |
|
25 |
-12,64 |
-1,76 |
Procedemos
a graficar los valores.
VPN ($)
Tasa de descuento requerida (%)
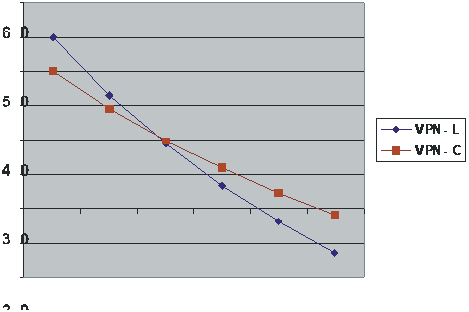
Igualando
las dos curvas obtenemos que se interceptan cuando el TIR= 8,5%.
2) Observe
la grafica del perfil del VPN sin hacer referencia a los VPN y a las TIR
reales. ¿Que proyecto o proyectos
deberían aceptarse si fueran independientes? ¿Y si fueran mutuamente
excluyentes? ¿Diferirán sus respuestas
de acuerdo con la tasa de descuento que se aplique? Explique que sus
respuestas.
Se debería aceptar el Proyecto C.
g) 1) ¿Cuál es la causa fundamental de los
conflictos de rangos que existen entre los criterios del VPN y de la TIR?
Generalmente se mide la riqueza de forma cuantitativa
en unidades monetarias, por lo que debería utilizarse el método del VPN para
lograr la maximización de la riqueza de los accionistas, el empleo del método
de la TIR podría conducir a decisiones de inversión que incrementen la riqueza,
pero no que la maximicen
2)
¿Qué es el “supuesto de la tasa de reinversion” y como le afecta a los
conflictos del VPN versus TIR?
El supuesto de la tasa de reinversion es una
suposición que afirma que los flujos de efectivo provenientes de un proyecto
pueden reinvertirse de acuerdo con 1) el costo de capital, si se utiliza el
método VPN, o 2) a la tasa interna de rendimiento, si se aplica el método TIR.
3)
¿qué método de presupuesto de capital debería utilizarse cuando el VPN y la
TIR proporcionan rangos conflictivos?
Explique su respuesta.
Cualquiera
de los dos métodos nos ofrece medidas de rentabilidad, pero cuando existan
rangos conflictivos es preferible tomar el TIR, ya que, este proporciona
información del margen de seguridad.
