Racionales:

(4/3)^4 = 3'16049...
22/7 = 3'14(285...)
311/99 = 3'141(414...)
(296/167)^2 = 3'14159(704...)   (Castellanos)
355/113 = 3'141592(9203...)
512/163 = 3'141(104)   (Stoschek)
103283/32876 = 3.14159265(1174...)

22/17 + 37/47 + 88/83 = (E. Pegg, 9 dígitos correctos)

Irracionales:

r(10) = 3.162277...
r(2) + r(3) = 3.146264... (utilizada para hacer una cuadratura del círculo aproximada)
20*r(2)/9 = 3.142696...
r(40/3-2*r(3)) = 3.141533... (viene del método de Kochanski para cuadrar el círculo) 
13*r(146)/50 = 3.14159195...
5/4 + r(229)/8 = 3.1415932438...
167/80 + r(10)/3 = 3.141592553389...

19*r(7)/16 = 3.14182968... 
7*(1 + r(3)/5)/3
9/5 + r(9/5) = 3.14164078...
(9^2 + 19^2/22)^1/4 = 3.141592652582... (Las cuatro últimas, de Ramanujan)

(77729/254)^1/5   (Castellanos)

ln(10691/462)   (Jerphanion)

Con la razón aúrea:

6/5*f² = 3'14164078...
4/r(f) = 3'144605... (Mircea-Mugurel) 

Con el número e:

(2*e³ + e⁸)^1/7 (Castellanos)

Con e y f:

5*f*e/7

Método de Kochanski

Se dibuja una circunferencia de radio R. Dentro de ella se inscribe un hexágono y se toma el triángulo OEG. Se traza una paralela al segmento EG que pase por A, prolongándola hasta que se corte con el segmento OE, obteniendo D. Desde el punto D y sobre ese segmento se transporta 3 veces el radio de la circunferencia y se obtiene el punto C. El segmento BC es aproximadamente la mitad de la longitud de la circunferencia.

Utilizando el teorema de Pitágoras y semejanza de triángulos es fácil demostrar que se obtiene una aproximación de pi con cuatro cifras decimales exactas.

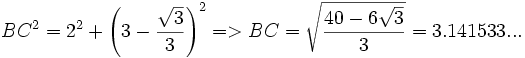
La distancia BC es una de las raíces del polinomio 9x⁴ - 240x² + 1492