The equations in this paper were derived mainly because the author has been kown to ask the question, "How was this equation derived?" In his time as a curious boy, not one toy was spared from being disected and reverse-engineered. On the other hand...

In the case of vented-box loudspeakers, ports are used to extend its low-frequency extension by using the energy at the rear side of the driver unit's cone. In the case of bandpass enclosures, ports are used to limit the passband of the loudspeaker system. Vented systems are known for being sensitive to design and construction errors or misalignments. The driver's Thiele-Small parameters should be as accurate as possible so that equations and CAD software can yield results that are most relevant to the driver and design parameters. We want to further reduce the chance of misalignment by carefully building the enclosure, but the question of port diameter and port length now arises.

As well as being a function of enclosure volume and vent radius, port length is also dependent on the speed of sound. Several books and Internet sites quote equations for port diameter and vent length, but nearly all of these equations assume the speed of sound to be 344m/s. It will be shown that the actual speed of sound is a significant factor in calculating the required port length. Although the effects on the enclosure's resonant frequency may be insignificant, the exact port length would be helpful in calculating enclosure dimensions. More so when enclosure size is critical.

It is often the case of the vent(s) being too long to fit in the accompanying enclosure. The builder has to reduce the port radius so that port length is consequently reduced, but in doing so the problem of port noise arises. Introducing flares to the port can significantly reduce port noise while still having practical port dimensions. However, the author has yet to see an equation for calculating the dimensions of flared vents. In this paper, an equation is presented that can be used to approximate the dimensions of flared ports.

1. Cylindrical Vents

In mechanical terms, a vented-box is simply a spring-mass resonant system. The air in the box acts as a spring and has a stiffness that is directly proportional to the port's area. On the other hand, the lump of air in the port acts as a lump of mass. The box resonant frequency can be calculated from the following equation.

where:
Fb - box resonant frequency (Hz)
Cmb - box compliance (m/N)
Mmp - port mass (kg)
pi = 3.1415926535897932384626433832795...

Cmb can be calculated from,

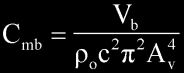
where:
Vb - net box volume (cubic meters)
po - density of air (kg / cubic meters)
c - speed of sound (m/s)
Av - port radius (m)

From the equation of Fb, we have the equation for Mmp (as a function of Cmb and Fb),

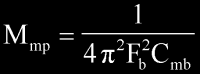
or

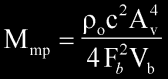
The speed of sound can be calculated from,

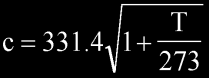
where T is the ambient temperatur in Celsius degrees. Now, the volume of air, Vp, in the cylindrical port can be calculated from the following equation.

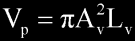
where Lv is the port length in meters. Since mass is equal to volume multiplied by density, the lump of mass in the port can be calculated from,

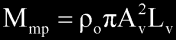
Manipulating this equation for Lv,

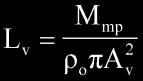
and since

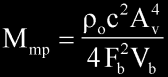
Lv simplifies to,

However, both ends of the cylindrical tube are actually loaded with a small mass of air. According to Beranek, the flanged end of a tube actually "extends" by 0.85*Av whereas the free end of the tube extends by 0.613*Av. Usually, the port is mounted flush against the loudspeaker baffle while the other end of the port is left unflanged, therefore the corrected equation for Lv is,

 

2. Multiple Cylindrical Vents

With high-power driver units, port noise can be an audible problem. A solution is to use a port with a larger vent radius. Alternatively, the builder may elect to use two or more vents when a single large vent is not readily-available or impractical to build.

From the Loudspeaker Design Cookbook (by Vance Dickason)

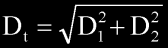
where:
Dt = effective diameter of the combined vents
D1, D2 = individual port diamter

For equi-diameter vents, D1 = D2, and so

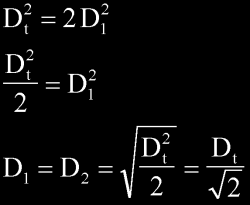
Now D = 2A, so

or in the case of N number of "equiradius" vents,

where Av is now the effective vent radius. Cmb for multiple vents is now,

Since all the ports have equal mass, each port will have mass equal to

Therefore each port length will be

For example, given:

c = 342.2m/s (at 18 degrees Celsius)
N = 2 ports
Av = 0.045m
Fb = 16Hz
Vb = 0.142 cubic meters

Each port length will be Lv = 0.972m (or 38.3inches)

If the ambient temperature happens to be 35 degrees Celsius (during summer), c increases to 352m/s

Consequently, Lv = 1.03m (or 40.7inches)

When only one vent is used, the change in port length (due to change in temperature) can be neglected. But when two or more vents are used, the change in ambient temperature has a significant change in port length.

3. Flared Vents

-- 22 June, 2002: Please note that this section of this page needs to be corrected. Apparently, the equation presented below over estimates the end-correction, so please disregard this section until the necessary corrections have been made. I apologize for any inconvenience this may have caused.

When the calculated port length is too long, given a particular enclosure size and tuning frequency, the builder may slightly decrease the vent radius, which will correspondingly reduce port length. Unfortunately, by doing so, port noise will almost certainly become a problem; to rectify the problem flared vents may be used.

First, we derive the equation for the volume of air in the flare. Pictured below is half of the cross section of a port's flared end (along with the derivation for the flare volume).

Fig. 1: Derivation of flare volume.

Rotating the shaded area about the y-axis gives the volume of air in the flare. The flare radius is a function of y and is given by the equation

A(y) = Am - sqrt(Af*Af - y*y)

where:
Am - mouth radius of the flare and is equal to Af + At
At - throat radius of the flare
Af - flare radius

When both ends of the cylindrical vent have flared ends like the one pictured below,

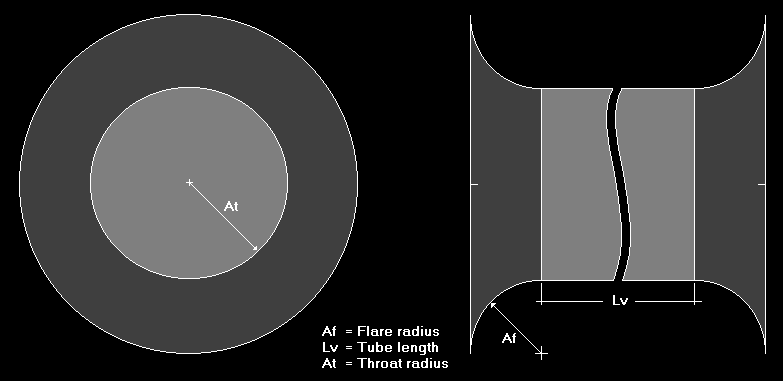
Fig. 2: Cylindrical vent with both ends flared.

The required tube length, Lt, can be calculated from

Lt = N*c*c*At*At / (4*pi*Fb*Fb*Vb) - 0.85*Am - 0.613*Am - 2*V / (pi*At*At)

and if only one end is flared,

Lt = N*c*c*At*At / (4*pi*Fb*Fb*Vb) - 0.85*Am - 0.613*At - V / (pi*At*At)

For example, given both ends are flared and:

c = 352m/s (at 35 degrees Celsius)
N = 1 port
At = 0.045m
Af = 0.0254m (1inch)
Fb = 16Hz
Vb = 0.142 cubic meters

Each port length will be Lv = 0.382m (or 15inches) as opposed to Lv = 0.483 (or 19inches) when no flares are used.

Assuming (just assuming) for a moment that air was incompressible, using the continuity equation for fluids,

At*At*vt = Am*Am*vm

where vt and vm are the fluid velocities at the throat and mouth respectively, we can calculate the appoximate exit velocity as

vm = At*At*vt / Am*Am = 7m/s

which translates to a 60% reduction in port velocity (assuming vt to be 17m/s or 5% the speed of sound). Halfway out the flare, the air velocity is 15m/s -- 12% down from 17m/s.

In practice, we can expect slightly higher exit velocities as air is not an ideal fluid.

4. Conclusion

A derivation for the general equation for port velocity is presented. It was shown that port length is not only dependent on port radius and net box volume, but also on the actual speed of sound. The effects on calculated resonant frequency may be neglected, but the effects of the change in the speed of sound on the port length cannot be ignored; especially when using two ore more ports.

An approximate equation for flared ports was presented. The presented equation may be used by builders to build their own flared vents when long cylindrical vents are impractical or when commercial flared vents are either too expensive or unavailable.

(corrections?)