I frattali non sono generati da chissà quale incomprensibile formula ma da semplici funzioni non-lineari: matrici e funzioni ricorsive.
Per questo motivo una piccola variazione delle variabili iniziali non genera automaticamente come siamo istintivamente portati a pensare un una piccola variazione delle variabili finali.
Per esempio sappiamo per certo che un pallone che cade lungo un declivio accidentato giungerà a un livello energetico minore (ad un punto più basso). Ma sappiamo anche che una leggera variazione delle condizioni iniziali cambiano radicalmente il percorso del pallone rendendo l’esperimento irriproducibile.
Un’altra proprietà fondamentale dei frattali è l’autosomiglianza. La diretta conseguenza dell’auto somiglianza è la dimensione frattale: particolarmente evidente nel “fiocco di neve di Koch”. La linea è come notiamo estremamente “frastagliata” usando un termine gergale: ringrandendo all’infinito c’è sempre una cresta più piccola. Questo ci porta credere che in qualche modo la curva occupi lo spazio e la sua dimensione sia quindi maggiore della dimensione di una curva e minore della dimensione di una figura piana.
La curva ha una dimensione 1 e la figura piana 2 di conseguenza la dimensione è tra 1 e 2.

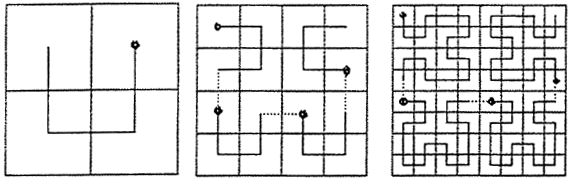
Un altro esempio più chiaro è la curva di Peano che occupa tutti i punti dell’area del quadrato.

I frattali in merito di queste caratteristiche possono riprodurre certi aspetti della natura in cui i classici triangoli, quadrati ed ellissi non sono più sufficienti. La forma delle nuvole delle onde, delle coste sono frattali e l’economia, la società e la linguistica sono descrivibili dalla teoria del caos.
La riscoperta del caos ci porta a vedere il mondo in maniera diversa. La natura non è più un equilibrio ordinato e rigido ma come direbbe Shakespeare è il:
“ Caos informe di graziose forme!”