Lembaran Kerja 1

HOME

TUGASAN BERNAS MATEMATIKKENALI BENTUKKU.....

Topik Berkaitan : Trigonometri ( Graf Fungsi Sinus )

Aras Berkaitan : Tingkatan 4 dan 5

Pengetahuan Sedia Ada : a)Nilai bagi sinus untuk 0 °£ x £ 360°

b)Sistem koordinat Cartesan ( x, y )

c)Amplitud dan frekuensi bagi graf trigonometri

Aras Kemahiran Menggunakan

Kalkulator Grafik : Tinggi

Masa : 60 minit

Jenis Tugasan : Pembinaan Konsep

Pendekaran Pembelajaran : Penyiasatan Koperatif

Objektif :

a) Pelajar-pelajar dapat mengenalpasti bentuk graf

] sinus melalui aktiviti penyiasatan dan perbincangan

dalam kumpulan.

b) Pelajar-pelajar dapat mengenalpasti perubahan-

perubahan dalam nilai a dan nilai b bagi fungsi

y = sin bx dan y = a sin bx

c) Pelajar dapat menggunakan perkaitan

dari aktiviti kumpulan untuk melakarkan graf sinus

yang lebih kompleks.

Bahan Bantu P-P : Kalkulator Grafik

]

Penerangan Tugasan Bernas Matematik

Dalam aktiviti ini pelajar-pelajar akan meramal beberapa bentuk graf sinus tanpa menggunakan kalkulator grafik . Kemudian pelajar dibenarkan menggunakan kalkukator grafik untuk menyemak dan melakar beberapa bentuk graf lain. Setelah menjalankan semua aktiviti pelajar dimimta membuat kesimpulan mengenai hubungan bentuk graf sinus,amplitud dan frekuensinya.

Aktiviti 1 ( y = sin bx )

Untuk membantu pelajar membuat penyiasatan pada landasan yang betul, mereka perlulah mengisi semua item-item yang dicatat dalam Lembaran Kerja 1. Sebagai contoh pelajar ingain meneroka bentuk graf sinus dan dari segi amplitud dan frekuensi.

Gerak Kerja:

1.Agihkan pelajar kepada kumpulan 4-5 orang dan tiap-tiap pelajar dibekalkan dengan kalkulator grafik.

2.Edarkan Lembaran Kerja 1(LK1)

3.Maklumkan pelajar untuk melengkapkan semua maklumat yang terdapat dalam LK1.

4.Pelajar haruslah diingatkan supaya membuat perbandigan dengan graf sinus y = sin x.

5.Semasa menjawab soalan 3 dan 4 para pelajar digalakkan berbincang dengan ahli kumpulan yang lain.

Aktiviti 2 ( y = a sin x )

Dalam aktiviti ini pelajar-pelajar diberi peluang untuk melihat perubahan-perubahan yang berlaku pada graf sinus apabila terdapat perubahan pada nilai a.

Gerak Kerja:

1.Dalam kumpulan yang sama,pelajar diminta melengkapkan Lembaran Kerja 2(LK2).

2.Pelajar-pelajar harus diingatkan supaya melakarkan graf terlebih dahulu sebelum menggunakan kalkulator grafik.

3.Guru hendaklah tidak sebarang komen tetapi boleh mengajukan soalan untuk menggalakkan pelajar berfikir seperti soalan ,

Bagaimana anda dapat membuat keputusan itu?

Bagaimana jika fungsi persamaan itu menggunakan nilai a yang lebih besar? atau sebaliknya?

4.Bahagian terakhir LK2 mengkehendaki pelajar mendapatkan fungsi persamaan yang sesuai supaya menghasilkan graf yang sama seperti di lampiran.

Aktiviti 3 ( y = a sin bx )

Dalam bahagian ini pelajar dikehendaki mengkaji amplitud, frekuensi dan koordinat titik maksimum.

Gerak Kerja :

1.Guru mengedarkan Lembaran Kerja 3 kepada setiap kumpulan.

2.Pelajar perlu melengkapkan semua maklumat yang dikehendaki sebelum menjawab soalan dibahagian 3 dan 4

3.Setelah menjalankan aktiviti di atas pelajar di minta berbincang dalam kumpulan untuk membuat kesimpulan terhadap apa yang diperhatikan.

Aktiviti Tambahan

Setelah semua kumpulan melengkapkan ketiga-tiga Lembaran Kerja, guru perlu memberi beberapa soalan yang berkaitan dan yang lebih mencabar untuk menggalakkan pelajar berfikir. Setiap wakil kumpulan di minta membentangkan hasil yang diperolehi.Minta pelajar melengkapkan semua item yang terdapat dalam Lembaran Kerja 4.

Lembaran Kerja 1 : y = sin bx

1. Ramalkan bentuk graf sin yang akan terhasil. Kemudian gunakan kalkulator grafik untuk menyemak lakaran graf anda.

Fungsi	Bentuk graf yang diramalkan	Semakan menggunakan kalkulator grafik
y = sin 2x
y = sin 0.5x
y = sin -x

2. Dengan menggunakan kalkulator grafik lakarkan graf bagi setiap fungsi dibawah dan lengkapkan jadual.

Fungsi	Lakaran bentuk graf	Nilai a dalam y = sin bx	Bentuk keluk berbanding graf y = sin x
y = sin 2x
y = sin 4x
y = sin 0.25x
y = sin -x
y = sin -4x

3. Terangkan perubahan-perubahan yang berlaku pada graf y = sin bx apabila nilai b berubah

Adakah nilai amplitud berubah apabila nilai b berubah ? Jika ya apakah perubahannya ?

...................................................................................................................................

.....................................................................................................................................

Adakah terdapat perubahan dari segi bentuk keluk berbanding graf y = sin x apabila nilai b berubah ( y = sin bx atau y = sin -bx )? Jika ya bagaimana perubahannya ?

...........................................................................................................................................

Adakah bilangan frekuensi berubah apabila nilai b berubah ? Jika ya bagaimana ?

....................................................................................................................................

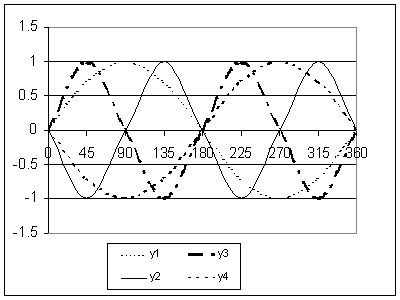
4. Apakah persamaan yang anda fikirkan sesuai untuk mewakili bentuk graf di bawah ? Cuba dapatkan bentuk graf dibawah dengan menggunakan kalkulator grafik anda.

Lembaran Kerja 2 : y = a sin x

1. Ramalkan bentuk graf sin yang akan terhasil. Kemudian gunakan kalkulator grafik untuk menyemak lakaran graf anda.

Fungsi

Bentuk graf yang diramalkan

Semakan menggunakan kalkulator grafik

y = 2sin x

y = -2 sin 0.5x

2. Dengan menggunakan kalkulator grafik lakarkan graf bagi setiap fungsi dibawah dan lengkapkan jadual.

Fungsi	Lakaran bentuk graf	Nilai a dalam y = a sin x	Koordinat titik maksimum	Bentuk keluk berbanding graf y = sin x
y = sin x
y = 3 sin x
y =0.5 sinx
y = - sin x

3. Terangkan apakah perubahan yang berlaku pada graf y = a sin x apabila terdapat perubahan pada nilai a ? Jika ya , kenapa perubahan ini berlaku ?

.................................................................................................................................

..................................................................................................................................

4. Apakah persamaan yang anda fikirkan sesuai digunakan untuk bentuk-bentuk graf di bawah. Gunakan kalkulator grafik untuk mendapatkan bentuk graf di bawah.

Lembaran Kerja 3 : y = a sin bx

1. Ramalkan bentuk graf sin yang akan terhasil. Kemudian gunakan kalkulator grafik untuk menyemak lakaran graf anda.

Fungsi

Bentuk graf yang diramalkan

Semakan menggunakan kalkulator grafik

y =2 sin2 x

y = - 0.5 sin 2x

2. Dengan menggunakan kalkulator grafik lakarkan graf bagi setiap fungsi dibawah dan lengkapkan jadual.

Fungsi	Lakaran bentuk graf	Nilai a dan b dalam y = a sin bx	Koordinat titik maksimum	Bentuk keluk berbanding graf y = sin x
y = sin x
y = sin 2 x
y = - 3 sin x
y = - 0.5 sin2 x
y = 4 sin x
y = 4 sin -x

3. Terangkan apakah perubahan yang berlaku pada graf y = a sin bx apabila a tetap dan b berubah.

.................................................................................................................................

Terangkan perubahan yang berlaku pada graf apabila b tetap dan a berubah

....................................................................................................................

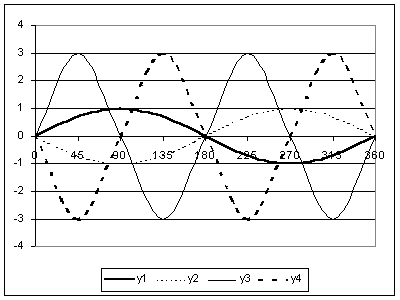
4. Apakah persamaan yang kamu perlu gunakan untuk mendapatkan bentuk graf seperti di bawah? Cuba gunakan kalkulator grafik untuk mendapatkan bentuk-bentuk graf seperti di bawah.

Lembaran Kerja 4 ( Aktiviti Tambahan)

1. Cuba lakarkan graf

a) y = sin x +2

b) y = sin x - 2

c) y = sin (x +45 )

d) y = sin ( x - 45)

2. Apakah kesimpulan yang dapat anda perhatikan pada graf di atas ?Bandingkan dengan graf y= sin x

............................................................................................................................

................................................................................................................................

3.Daripada semua aktiviti yang telah dijalankan apakah hubungan antara frekuensi dengan pekali x dalam y = sin bx

...........................................................................................................................