15 PUZZLE
The 15 Puzzle was introduced by Sam Loyd in the nineteenth century.
The puzzle consists of 15 sliding tiles numbered from 1 to 15 and an
empty space.From any initial configuration the goal is to get the tiles
by sliding one at a time to the following configuration.
| 1
| 2
| 3
| 4
|
| 5
| 6
| 7
| 8
|
| 9
| 10
| 11
| 12
|
| 13
| 14
| 15
|
|
Now the question arises that can we get to this configuration from
any arbitrary initial configuration.The answer is no.The puzzle can
only be solved iff the number of inversions is even.If a bigger number
precedes a smaller number(counting from left to right &top to bottom)
it is said to be an inversion.The total number of inversions N given by

where
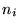 =number of inversions corresponding to i.
=number of inversions corresponding to i.
This will become clear from the following example.Consider the configuration below
| 3
| 1
| 2
| 4
|
| 6
| 5
| 7
| 8
|
| 9
| 10
| 11
| 12
|
| 13
| 14
| 15
|
|
Here n3=2(because 3 precedes 1 and 2)
n6=1(because 6 precedes 5)
For all other i ni=0
Therefore total number of inversions N=2+1=3
As N=3(odd) this configuration can never be solved.
Click here to return to the applet.

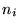 =number of inversions corresponding to i.
=number of inversions corresponding to i.