BINOMIAL OPTION PRICING
Binomial tree is a useful and a very popular technique for pricing a stock option. This tree represents different possible paths that might be followed by the stock price over the life of the option.
Introduction to Binomial Tree Concept:
To get an idea about the binomial model, let us consider very simple situation where a stock price is currently 2000 TL and it is known that at the end of three months the stock price either will be 2200 TL or 1800 TL. We suppose that we are interested in valuing a European call option to buy the stock for 2100 TL in three months. This option will have one of the two values at the end of three months. If the stock price turns out to be 2200 TL, the value of the option will be 100 TL; if the stock price turns out to be 1800 TL, the value of the option will be zero. The situation is illustrated below.
Stock Price = 2200 TL
Option Price = 100 TLStock Price=2000TL
Stock Price = 1800 TL
Option Price = 0 TL
The only assumption we need is that there are no arbitrage opportunities for an investor in binomial option pricing. We set up a portfolio of the stock and the option in such a way that there is no uncertainty about the value of the portfolio at the end of the three months. We then argue that, since the portfolio has no risk, the return earned on it must equal the risk-free interest rate. This enables us to work out the cost of setting up the portfolio and therefore the option's price. Since there are two securities (the stock and the stock option) and only two possible outcomes, it is always possible to set up the riskless portfolio.
Consider a portfolio consisting of a long position in D shares of the stock and a short position in one call option. We will calculate the value of D that makes the portfolio riskless. If the stock price moves up from 2000 to 2200, the value of the shares is 2200D and the value of the option is 100 so that the total value of the portfolio is 2200D - 100. If the stock price moves down from 2000 to 1800, the value of the shares is 1800D and the value of the option is zero so that the total value of the portfolio is I800D . The portfolio is riskless if the value of D is chosen so that the final value of the portfolio is the same for both of the alternative stock prices. This means:
2200D -100 = 1800D or D = 0.25
A riskless portfolio is, therefore:
Long: 0.25 shares, Short: 1 option
If the stock price moves up to 2200, the value of the portfolio is:
2200 x 0.25 - 100 = 450
If the stock price moves down to 18, the value of the portfolio is:
800 x 0.25 = 450
Regardless of whether the stock price moves up or down, the value of the portfolio is always 450 at the end of the life of the option.
Riskless portfolios must, in the absence of arbitrage opportunities, earn the risk-free rate of interest. Suppose that in this case the risk-free rate is 78 percent per annum. It follows that the value of the portfolio today must be the present value of 450 or 450 e-0.78*0.25 = 370.27
The value of the stock price today is known to be 2000. Suppose the option price is denoted by f. The value of the portfolio today is, therefore,
2000 x 0.25 - f = 500 - f
It follows that
500 - f = 370.27 or f = 129.73
This shows that in the absence of arbitrage opportunities the current value of the option must be 129.73 TL. If the value of the option were more than 129.73, the portfolio would cost less than 370.27 to set up and would earn more than the risk-free rate. If the value of the option were less than 129.73, shorting the portfolio would provide a way of borrowing money at less than the risk-free rate.
We can generalise the argument that has just been presented by considering a stock whose price is S and an option on the stock whose current price is f. We suppose that the option lasts for time T and that during the life of the option the stock price can either move up from S to a new level Su or down from S to a new level Sd (u >1;d< 1). The proportional increase in the stock price when there is an up movement is u - 1; the proportional decrease when there is a down movement is 1 - d. If the stock price moves up to Su, we suppose that the payoff from the option is fu; if the stock price moves down to Sd, we suppose the payoff from the option is fd. The situation is illustrated below.
Su
fu
S
f
Sd
fd
As before we imagine a portfolio consisting of a long position in D shares and a short position in one option. We calculate the value of D that makes the portfolio riskless.
If there is an up movement in the stock price, the value of the portfolio at the end of the life of the option is: Su D - fu
If there is a down movement in the stock price, this becomes: Sd D - fd
The two are equal when SuD - fu = SdD - fd or D = ( fu - fd ) / ( Su - Sd )
In case the portfolio is riskless and must earn the risk-free interest rate. D is the ratio of the change in the option price to the change in the stock price as we move between nodes.
Denoting the risk-free interest rate by r, the present value of the portfolio must be :
[ SuD - fu ] e-rT
The cost of setting up the portfolio is: SD - f
It follows that: SD - f = [ SuD - fu ] e-rT
Substituting D and simplifying, this equation reduces to
f = e-rT [ pfu + (1-p)fd ] where p = ( e-rT - d ) / ( u - d )
Although we do not need to make any assumptions about the probabilities of up and down movements, it is natural to interpret the variable p as the probability of an up movement in the stock price. The variable 1-p is then the probability of a down movement and the expression: p fu + ( 1 - p ) fd is the expected payoff from the option. With this interpretation of p, the value discounted at the risk-free rate.
We now investigate the expected return from the stock when the probability of an up movement is assumed to be p. The expected stock price at time T, E(ST), is given by:
E(ST) = pSu + (1 - p)Sd or E(ST) = pS(u - d) + Sd
Substituting for p, this reduces to: E(ST) = SerT
showing that the stock price grows on average at the risk-free rate. Setting the probability of the up movement equal to p is, therefore, equivalent to assuming that the return on the stock equals the risk-free rate.
It will be referred to a world where all individuals are risk neutral as a risk-neutral world. In this world investors require no compensation for risk and the expected return on all securities is the risk-free interest rate. An important general principle in option pricing is known as risk-neutral valuation. This means that we can only use Binomial Model iff the world is risk neutral. The expected return on all stocks in a risk-neutral world is the risk-free rate.An option can be valued in a risk-neutral world by discounting its expected payoff at the risk-free rate.
The analysis shows that the principle of risk-neutral valuation applies to options when they are valued using binomial trees. It is assumed a risk-neutral world when we set the probability of an up movement to p.
The Binomial Model For A NonDividend-Paying Stock
Consider the evaluation of an option on a nondividend-paying stock. We start by dividing the life of the option into a large number of intervals of lenght D t. It is assumed that in each time intervals the stock price moves from its initial value of S to one of two new values, Su and Sd. This model is illustrated in the following figure.
Su
p
S
1 - p
Sf
In general, u > 1 and d < 1. The movement from S to Su is, therefore ‘up’ movement and the movement from S to Sf is, therefore ‘down’ movement. The probability of an up movement is assumed to be p and probability of a down movement is assumed to be 1 - p.
The parameters p, u and d must give corect values for the mean and the variance of the stock price during a time interval D t. Since we are working in a risk neutral world, the expected return from a stock is the risk-free interest rate, r. Hence, the expected value of the stock price at the end of time interval D t is SerD t, where S is the stock price at the beginning of the time interval. It follows that
SerD t = pSu + ( 1-p )Sd or erD t = pu + ( 1-p )d
The standard deviation of the proportional change in the stock price in a small time interval D
t is ![]() . This means that the variance of the actual change in D
t is S2s
2D
t. Since the variance of a variable Q is defined as E (Q2) - E(Q)2, where E denotes expected value, it follows that
. This means that the variance of the actual change in D
t is S2s
2D
t. Since the variance of a variable Q is defined as E (Q2) - E(Q)2, where E denotes expected value, it follows that
S2s 2D t = pS2u2 + (1-p) S2d2 - S2 [ pu + ( 1-p )d]2
or
s 2D t = pu2 + (1-p) d2 - [ pu + ( 1-p )d]2
So by using these formulas provided that D t is small, we can detect p, u and d as follows:
p = ( a -d ) / ( u - d )
u = es Ö D t
d = 1/es Ö D t where
a = erD t
All of these equations are correct to be using no-arbitrage arguments as well as risk-neutral valuation arguments.
The complete tree of stock prices that is considered when the binomial model is used is illustrated in figure(a). At the time zero the stock price S is known. At time D t, there are two possible stock prices, Su and Sd; at time 2D t, there are three possible stock prices, Su2, S, and Sd2; and so on. In general at time iD t, i+1 stock prices are considered . These are:
Sujdi-j j = 0,1,2….,I
It is noted that the tree recombines in the sense that an up movement followed by a down movement leads to the same stock price as a down movement followed by an up movement. This considerably reduces the number of nodes on the tree.
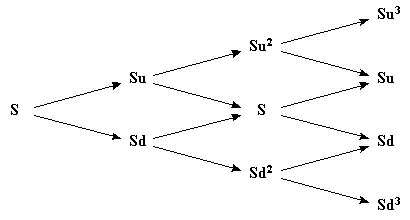
figure(a)
Working Backward Through The Tree:
Options are evaluated by starting at the end of tree (time T) and working backward. The value of the option is known at time T. For example, a put option is worth max
(X - ST ,0) and a call option is worth max (ST - X,0), where ST is the stock price at time T and X is the strike price. Since a risk-neutral world is being assumed, the value at each node at time T - D t can be calculated as expected value at time T discounted at rate r for a time period D t. Similarly, the value at each node at time T - 2D t can be calculated as the expected value at time T - D t discounted for a time period D t at rate r, and so on. If the option is American, it is necessary to check at each node to see whether early exercises is preferable to holding the option for a further time period D t. Eventually, by working back through all the nodes, the value of the option at time zero is obtained.
An Example:
The basic idea is best illustrated with an example. Consider a six month American Put option on a nondividend-paying ISE-100 Index when the index level is 15000 TL, and the strike price 18000 TL, the risk-free interest rate is 40 percent per annum, and the volatility is 0.4851 per annum. Suppose that we divide the life of the option into 8 interval of lenght 0.75 month ( = 0.062475 ) for the purposers of constructing a binomial tree. Then D t = 0.062475 and using proper equations:
u = 1.128908 d = 0.885712 a = 1.1051 p = 0.902264 1-p = 0.097736
Figure at below shows the binomial tree. At each node there are two numbers. The top one shows the index level at the node; the lower one shows the value of the option. For example, the stock price at the shaded cell; 15000*1,1289*0,88582 =13287. The option prices at the final nodes are calculated as max ( X - ST , 0 ). For example, the option price at the right bottom node 11580 TL.
|
35051,04 |
|||||||
|
31048,63 |
0 |
||||||
|
27503,24 |
0 |
27503,24 |
|||||
|
24362,7 |
0 |
24362,7 |
0 |
||||
|
21580,77 |
0 |
21580,77 |
0 |
21580,77 |
|||
|
19116,5 |
0 |
19116,5 |
0 |
19116,5 |
0 |
||
|
16933,62 |
-1116,5 |
16933,62 |
-1116,5 |
16933,62 |
0 |
16933,62 |
|
|
15000 |
1066,381 |
15000 |
1066,381 |
15000 |
1066,381 |
15000 |
1066,381 |
|
3000 |
13287,18 |
6000 |
13287,18 |
6000 |
13287,18 |
6000 |
13287,18 |
|
4712,823 |
11769,94 |
4712,823 |
11769,94 |
4712,823 |
11769,94 |
4712,823 |
|
|
6230,061 |
10425,95 |
6230,061 |
10425,95 |
6230,061 |
10425,95 |
||
|
7574,049 |
9235,431 |
7574,049 |
9235,431 |
7574,049 |
|||
|
8764,569 |
8180,854 |
8764,569 |
8180,854 |
||||
|
9819,146 |
7246,697 |
9819,146 |
|||||
|
10753,3 |
6419,21 |
||||||
|
11580,79 |
Using The Binomial Tree For Options On Indexs With Dividend Yield
Since the dividends provide a return of q, the stock price itself must on average in a risk-neutral world provide a return r - q. Hence,equations becomes:
Se(r-q)D t = pSu + ( 1-p )Sd or e(r-q)D t = pu + ( 1-p )d
and a = e(r-q)D t
The binomial tree numerical procedure can, therefore, be used exactly as before with this new value of a.