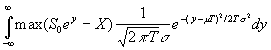
The Black-Scholes model is the first analytical model developed for pricing options which has been introduced in an article in the “Journal of Political Economy” by Myron Scholes and Fisher Black in the May-June edition in 1973. Since its publication, it has had a huge influence on the theory of finance and the way in which market participants price and hedge options. In our project, most of the option pricing applications are based on the Black-Scholes model. Although some of the assumptions of the model are very strong and sometimes unrealistic, by making a few adjustments, the model allows it to relax some of these assumptions in order to extend the real-world applicability of the model. Thus, the model is flexible and is still the most commonly accepted and used by practitioners and scientists for pricing options. More importantly, the assumptions used in the derivation of the model has provided the theoretical foundation upon which other option pricing models and pricing models for other derivative securities (options where the underlying asset is not a common stock) have been developed. In this part of the second chapter, the Black-Scholes option pricing model will be defined in its broad scope in a rigorous fashion. The limitations, simplifications and idealizations as well as the advantages of the model will be explained. In the project, before attempting to use the Black-Scholes model in our applications, we scrutinized the major assumptions of the model and tested the validity of some of them.
As explained, there are six factors or inputs that affect the price of a particular option: 1) The price of the underlying asset, 2) The exercise price, 3) The time to expiration, 4) The volatility of the price of the underlying asset, 5) The risk-free interest rate and 6) The dividends expected during the life of the option. In its original form, the Black-Scholes model values an option as a function of the first five variables and assumes that the option can be exercised at the expiration date only and the underlying asset is a common stock. Thus, it is an exact analytic pricing model for European options on nondividend-paying stocks. By making certain adjustments, the model can be extended to price European options on dividend-paying stocks and all types of American call options, but it provides no exact analytic solution for the value of American put options because, in general, it is optimal to exercise American put options before their expiration dates which make them more valuable than the Black-Scholes price for European put-options.
4.1.2.1.The Stochastic Process For The Underlying Security Price :
In the Black-Scholes model, the assumptions for the stochastic process for the underlying asset are crucial, since the two of the input variables of the model define the underlying security price-process. In addition, two other major assumptions of the model which will be explained later( the no-arbitrage assumption and the risk-neutrality assumption) and lead to the derivation of the model can be validated only if we make the assumption that the stochastic process governing the movement of stock prices is a continuous-time stochastic process. More specifically, it is assumed that stock prices follow a geometric Brownian motion process which is also called the Ito process or Markov diffusion process in the literature. Next, this assumption will be discussed in full detail.
A stochastic process {X(t), t >= 0} is said to be a Brownian motion process if
(i) X(0) = 0;
(ii) {X(t), t = 0}has stationary and independent increments: Cov[ D Xt , D Xt+k ] = 0 and the
distribution of X(t+s) - X(t) depends only on s but not on t.
(iii) X(t) is normally distributed with mean 0 and variance s 2 t : X(t) ~ N( 0, s 2 t )
Basically, the Brownian motion is the limiting case of the random walk process. When s = 1, the process is called standard Brownian motion. Any Brownian motion can be converted to the standard process by letting B(t) = X(t) / s . Moreover, X(t) is a continuous function of t and by the independent increment assumption, it follows that for all t1 < t2 <.....< tn , X(t1), X(t2) - X(t1), ......, X(tn) - X(tn-1) are independent , by the stationary increment assumption it follows that X(tk) - X(tk-1) is normally distributed with mean 0 and variance tk - tk-1.
The Brownian motion can be obtained in the following way: We consider a symmetric random walk process which in each time unit is equally likely to take a unit step either in the positive direction or in the negative direction. That is, the random walk process is a Markov chain with
Pi, i+1 = 0.5 = Pi, i-1 where i = ....,-1,0,1,......
In the limit, if the process is speeded up by taking smaller and smaller steps in smaller and smaller time intervals the random walk process converges to the Brownian motion process. More formally, if the random walk process takes in each D t time unit a step of size D x either to the positive or negative direction with probability 0.5 and if we let X(t) denote the position at time t then:
(1) X(t) = D x ( X1 + ... + X [ t / D t ] )
where Xi = 1, if the i th step of length D x is to the positive direction
Xi = -1, if the i th step of length D x is to the negative direction
and [ t/D t ] is the largest integer less than or equal to t/D t, and Xi are assumed
independent with P{Xi = 1}= P{Xi = -1}= 0.5
Thus, since E[ Xi] = 0, Var(Xi) = E[ Xi 2] - E2[ Xi] = E[ Xi 2] = 1, we see from (1) that
(2) E [ X(t)] = 0 and Var(X(t)) = (D x)2 [ t/D t ]
In order to obtain the limiting process we have to let both D x and D t go to 0. To keep the resulting limiting process nontrivial, we let D x = s sqrt(D t) for some positive constant s . One can see from (2) that as D t ® 0:
E [ X(t)] = 0 Var(X(t)) ® s 2 t
From the central limit theorem which states that the sum of independently and identically distributed random variables is a normal random variable and from (1), X(t) is normally distributed with mean 0 and variance s 2 t : X(t) ~ N( 0, s 2 t ).
(3) X(t) = 0 + s sqrt(D t) z where z ~ N( 0, 1)
In addition, since the changes of value of the random walk in nonoverlapping time intervals are independent and the distribution of the change in position of the random walk over any time interval depends only on the length of that interval, it follows that {X(t), t= 0} has independent and stationary increments as stated above in the definition of the Brownian motion process which is also called the Wiener process.
In the previous paragraphs, it has been suggested that the Black-Scholes model assumes that stock prices follow a geometric Brownian motion process. Thus, there are variations on the basic Brownian motion process. Now, these variations and their implications will be discussed.
The first variation is the Brownian motion with drift. {X(t), t= 0} is said to be a Brownian motion process with drift coefficient m and variance parameter s 2 if
(ii) {X(t), t= 0} has stationary and independent increments: Cov[ D Xt , D Xt+k ] = 0 and the
distribution of X(t+s) - X(t) depends only on s but not on t.
(iii) X(t) is normally distributed with mean m t and variance s 2 t: X(t) ~ N(m t , s 2 t )
Thus, X(t) = m t + s sqrt(t) z where z ~ N(0,1)
(X(t) - m t) / s = 0 + sqrt(t) z = B(t) (Note that B(t) is the standard Brownian motion.)
Hence, an equivalent definition of the Brownian motion drift will be as follows:
X(t) = m t + s B(t)
If {X(t), t= 0} is a Brownian motion process with drift coefficient m and variance parameter s 2 , then the process {S(t), t= 0} defined by
S(t) = e X(t) is called a geometric Brownian motion process.
Given the history of the process up to the current time t0 , the expected value of the process at time t ( t > to ) can be computed as follows:
E[ S(t) | S(u), 0 £ u £ t0 ] = E[ e X(t) | S(u), 0 £ u £ t0 ]
= E[ e X(t
0) + X(t) - X(t0) | S(u), 0 £ u £ t0 ]= e X(t
0) E[ e X(t) - X(t0) | S(u), 0 £ u £ t0 ]= S(t
0) E[ e X(t) - X(t0) ]The next to last equality follows from the fact that X(t0) is given, and the last equality follows from the independent increment property of Brownian motion. Since by the definition of the Brownian motion (stationary increments), X(t) - X(t0) is normal with mean m (t - t0) and variance (t - t0)s 2 and from the moment generating function of a normal random variable, it follows that
E[ e X(t) - X(t
0) ] = e m (t - t0) + (t - t0)s 2 / 2Thus, E[ S(t) | S(u), 0 £ u £ t0 ] = S(t
0) e (m + s 2 / 2) (t - t0) (4)Geometric Brownian motion is useful in the modeling of stock prices over time when the percentage changes in stock prices are independent and identically distributed, since the Brownian motion requires the independence and stationarity of the increments where log(S(tk)) - log(S(tk-1)) is normal with mean m (tk - tk-1) and variance (tk - tk-1)s 2 and from simple algebra we know that
log(S(tk)) - log(S(tk-1)) = log (S(tk) / S(tk-1))
Therefore, geometric Brownian motion property requires that
log (S(tk) / S(tk-1)) ~ N(m (tk - tk-1) , s 2 (tk - tk-1)) (5)
or log( St + D t / St ) ~ N(m D t , s 2 D t ) where tk-1 = t and tk - tk-1 = D t
Thus, if a certain variable St follows a geometric Brownian motion then log(St) follows a Brownian motion and both log( St ) and log( St + D t / St ) are normally distributed. Thus, the geometric Brownian motion is equivalent to the lognormal probability distribution. Therefore, in the literature, the continuous stochastic process that the Black-Scholes model proposes for explaining the stock price process is called both geometric Brownian motion and the lognormal distribution. We had stated that geometric Brownian motion can be used to model stock prices if one is certain about the assumption that the percentage changes in stock prices are independent and identically distributed. For example, suppose that Sn is the price of some stock at time n and Sn / Sn-1 , n = 1, are independent and identically distributed. If we let Rn = Sn / Sn-1 then
Sn = Rn Rn-1 .... R1 S0 Thus, log ( Sn ) = å log ( Ri ) + log ( S0 )
Hence, if log ( Ri ) are independent and identically distributed, {log ( Sn )}will be a Brownian motion with drift, and {Sn } will be a geometric Brownian motion and the Brownian motion property requires that {log ( St + D t / St )} are normally distributed. Thus, in order to prove the hypothesis that stock prices follow a geometric Brownian motion or that they are lognormally distributed, one must show that proportional changes(logarithmic returns which are also called continuously compounded returns) in stock prices in a short period of time are i.i.d normally distributed in order to apply the Black-Scholes option pricing model.
Having made the above explanations and derivations about the stochastic process assumed by the Black-Scholes model to govern the security price movements , one must explain the meaning of the parameters used in the equations above and their relevance to the underlying asset on which the option is written.
In the above steps, we can make the following substitution:
Let t denote the current time instead of t0 (In the paragraphs above, we used t0 to denote the current time and t to denote a future time point) where t = t0 . Then, a time point in the future can be referred to as t + D t. Having made this change of notation, we can assert that we had shown the following equations above and list the parameters used in them. From (4) and (5) and the change of notation, we get
(6) E[ S(t + D t) | S(u), 0 £ u £ t ] = S(t) e (m + s
2 / 2) D t = S(t) e a D t or equivalently,log( St + D t / St ) = m D t + s sqrt(D t) z
where
St + D t / St = the return of the stock over the instant t to t + D t.
m = a - s
2/2 = the mean continuously compounded stock return per unit timea = the geometric mean stock return per unit time ( expected return on the stock over [ t, t + D t] )
s = the standard deviation of the continuously compounded stock return per unit time
z = the standard normal random variable with mean 0 and standard deviation 1.
The second equation of (6) can be expanded further to arrive at another conclusion:
log( St + D t / St ) = m D t + s sqrt(D t)z
St + D t / St = e m D t + s sqrt(D t) z
1 + D St / St = 1 + (m D t + s sqrt(D t)z) + (m D t + s sqrt(D t)z)2 / 2 + .....
where D St = St + D t - St and ex = 1+ x + x2 / 2 + x3 / 6 + .....Collecting the terms and ignoring terms in the expansion of higher order than D t , we get
D St / St = s sqrt(D t)z + (m + s 2 z2 / 2)D t
E[ D St / St ] = (m + s 2 /2)D t + .... since E[ z2 ] = 1
var[ D St / St ] = s 2D t
From the central limit theorem, D St / St = (m + s 2 /2)D t + s sqrt(D t) z (7)
Finally, as D t approaches zero, (7) can be expressed as follows:
dS / S = (m + s 2 /2)dt + s sqrt(dt) z (8)
dS / S = a dt + s sqrt(dt) z
In our project, we tested the assumption that stock prices follow a geometric Brownian motion for the case of ISE-30 index and some of its 30 constituent common stocks. To test this assumption, we applied the chi-square test to see whether the continuously compounded returns log (St / St-1) are normally distributed. For the ISE-30 index, we used a sample of 200 logarithmic returns which are obtained from the index level data between . To apply the chi-square test, we have constructed 20 classes of equal probability of 0.05 which is greater than the minimum class number of sqrt(200) and less than the maximum class number of 200/4 = 50. The expected frequency for each class was 10 = 200*0.05. We constructed the test with a confidence level of 99.5% and since the expected return and the standard deviation are estimated from the data, the degree of freedom was 17. We obtained the following result for the ISE-30 index:( See also the appendix)
H0 : Logarithmic index returns are normally distributed.
H1 : Logarithmic index returns are not normally distributed.
The critical value is c 20.995, 17 = 35.7
Since our test statistic c 2
0 = 34.9 < c 20.995, 17 = 35.7, we could not reject H0 , but this result does only suggest that we cannot reject H0 with a high b -risk of making a Type-II error since the confidence level a is extremely high with 99.5% and the critical value c 20.995, 17 = 35.7 barely exceeds the test statistic of c 20 = 34.9. Thus, the power of the test is questionable but the test gave a much better result for the ISE-30 index compared with the test results of stocks comprising the index.For instance, for the case of Akbank common stock, we obtained the following result from the chi square test. We designed the chi-square test for the Akbank case in the same way as we constructed the test for the ISE-30 index with a sample size of 200, a class number of 20 and a confidence level of 99.5%. But the test statistic c 2
0 = 193.2 was clearly much higher than the critical value of c 20.995, 17 = 35.7. So, one can surely reject the H0 hypothesis for the price movements of Akbank common stock. The chi-square test gives the same result for the returns of all of the 30 common stocks listed in the ISE-30. But for the ISE-30 index, we can’t reject the null hypothesis in certain choices of the test parameters. Thus, according to the results of the chi-square tests, it is more likely that the normality of stock returns assumption is valid or approximately valid for the ISE-30 index.Actually, this result is consistent with the real world behavior of common stock prices where discontinuities and large discrete jumps in stock prices or index levels can be observed at certain times. However, the Black-Scholes model assumes that the underlying security price process is a continuos time process where historical stock prices can be graphed continuously as a function of time. But in reality, there are instances where stock prices or index levels move with discrete (modest or large) jumps rather than by changing continuously which may account for the fact that stock or index returns could have skewed probability distributions rather than a normal distribution. The general effect of jumps is that extreme outcomes become more likely and in particular, price jumps can be observed for individual stocks more frequently compared with an index where the effect of single, large discrete jumps in one or more of the stocks comprising the index can be reduced or compensated by the price movements of other stocks comprising the index. Thus, in general, index levels change “more continuously” compared with individual stocks but in cases of sudden market upturns or downturns after the receipt of a new information to the market, index levels can also change by making large discrete jumps. Thus, we can say that the results of the chi-square test for the ISE-30 index and its constituent stocks coincide with these arguments about the stochastic process governing the price movements.
Another major assumption of the Black-Scholes model about the underlying stochastic process is that the variability of logarithmic stock returns s is constant during the life of the option. However, the empirical evidence of previous studies in the field suggests that a constant volatility assumption is a poor reflection of the reality. The volatility with which investors are concerned when pricing an option is the future level of the stock volatility between the current time and the expiration date of the option. In order to estimate this volatility, we rely on the assumption that the volatility is constant and calculate it from the mean and the variance of the historical logarithmic stock returns. But in reality, the volatility of stock returns tends to change over time partly in response to the level of stock prices or the index level and due to the substantial day-of-the week effects(i.e. weekends, and holiday). One of the strongest departure from this assumption is that the stock variance increases as the stock price falls . In addition, depending on the receipt of a new information in the market( profit/loss declarations of firms, insider trading, financial, economical or political crises, wars etc.) the volatility of the market prices can increase suddenly at certain times for a certain period of time. Thus, the assumption of constant price volatility is not a very strong assumption about the underlying stochastic process for the underlying asset when we consider the ISE where the volatility increases or decreases suddenly depending on the political and economic situation (e.g. 1994 economic crisis, changes of governments or declaration of general elections, gulf crisis in 1990, Asia financial crisis in 1997 etc.) and also as a result of insider trading which is still a common fact of the Turkish capital market.
4.1.2.2. The Absence Of Arbitrage Opportunities And The Perfect Hedge Assumption
The price of an option must be set up in such a way so that no arbitrage is possible. This assessment is the most fundamental assumption of all types of option pricing models. In first part, using no arbitrage arguments, we had shown that one can determine lower and upper bounds for option prices and prove the put-call parity theorem for European options without making any assumptions about the underlying stochastic process. Similarly, by using only the no arbitrage argument, we will prove that a European call option on a nondividend-paying stock will never be exercised early and that a European and American call option on a non-dividend paying stock must have the same value.
The meaning of arbitrage is to be able to guarantee a sure win or riskless profit regardless of the future state of prices or future outcomes of the price processes in the markets. If an option is not fairly priced, namely if it is underpriced or overpriced, some shrewd investors can realize riskless or sure profits without incurring any risks by trading the options or combinations of options with other financial instruments like the underlying asset, futures, bonds etc. (examples of making arbitrage are given in Part A of the second chapter when determining upper and lower bounds for option prices and when proving the put-call parity theorem. Other arbitrage examples will be given later where we will deal with certain properties of European and American call options). Thus, if arbitrage opportunities exist at a certain option price, this price will not be the market-equilibrium price and change as a result of the actions of arbitrageurs. Thus, the possibility of permanent arbitrage opportunities is not desirable in efficient capital markets because they unfairly distort the pricing process which is the benchmark used in allocating and partitioning limited economical resources according to the fair value or real performance of the market participants. Therefore, in order to determine the exact and fair numerical value for the price of the option, one must derive the option price in such a way so that arbitrage opportunities are eliminated from the outset.
The Black-Scholes model is derived by directly using the no-arbitrage argument. In order to use this argument, another fundamental assumption of option pricing is brought into the play: the perfect hedge assumption. The perfect hedge assumption states that, if the underlying stochastic price process is a continuous time process, then it is possible to set up a riskless portfolio by combining the option and the underlying asset. In order to create this portfolio which duplicates the payoff of a riskless bond over the time until expiration [ t, T] , we note that the option’s exposure to the underlying asset at every instant time is simply the first derivative of the call price with respect to the price of the underlying asset. This derivative is referred to as the perfect hedge ratio or the delta D of the option. This ratio indicates the change in the option price as a result of a unit change in the price of the underlying asset.Then (for example the underlying asset is a stock and the option is a call option written on this stock), for a very short period of time, a riskless portfolio can be set up by taking a short position in 1 call option and a long position of D shares of stock( or D units of the underlying asset). For an instantaneously short period of time, this portfolio remains riskless since any profit (or loss) from the underlying asset is exactly offset with a loss(profit) from the option position. But to remain riskless until the expiration of the option, the portfolio must be rebalanced continuously since the perfect-hedge ratio or the delta D of the option changes with time. In order to do this, the delta D or the perfect hedge ratio can be recalculated instantaneously and the hedge rebalanced by adjusting the position in the underlying asset or the option. So, the hedge portfolio can in theory be maintained risklessly until expiration where the gain or loss from the stock(underlying asset) always offsets the gain or loss from the option position so that the overall value of the perfect-hedge or the so called riskless portfolio at any time point during the life of the option is known with certainty. Thus, to create a riskless portfolio is theoretically possible since we know that, for an instantaneously short period of time, the price of the option is perfectly correlated with the price of the underlying asset and they both depend on the same underlying source of uncertainty.
Now, one can use the no arbitrage argument to price an option in the following way. Since the perfect hedge portfolio is riskless the value of this portfolio at any time point can be known with certainty. Thus , since the portfolio has no risk, the return earned on this portfolio must be equal to the riskfree interest rate which is the rate of return earned on a riskless government bond. If this were not true, then there would be an arbitrage opportunity between the short-term bond market on the one hand and the option and stock markets on the other hand. Then, by using this argument, the value of the riskless portfolio at the expiration date can be discounted at the risk free interest rate to determine the initial cost of setting up the perfect hedge. Since the current price of the underlying asset is already known, the option price can be calculated from the cost of setting up the riskless portfolio. In their original paper, Black and Scholes derived their model by using these arguments.
However, a sufficient condition for the existence of a perfect hedge is that the underlying stochastic security price process is continuous time process. Thus, one has to restrict the class of feasible stochastic processes allowed for stock prices, since even when considering only small time intervals, sudden and discontinuous jumps in stock prices make it impossible to create a perfect hedge. The geometric Brownian motion process which is assumed by the Black-Scholes model to govern the price movements rules out the possibility of sudden, discontinuous jumps since it is a continuous-time diffusion and is said to have a continuous-sample path. This continuity allows the construction of an instantaneous, perfectly hedged portfolio.
Other scientists proposed other continuous-time and discontinuous stochastic processes which account for the fact of modest price jumps in reality( continuous jump process studied by Cox and Ross, and Merton’s jump diffusion process which is a mix of a continuous-sample path process(diffusion) and a discontinuous-sample path process(jump)).
4.1.2.3. The Risk Neutrality Assumption
The ability to construct a perfect hedge is crucial in the option pricing theory as stated in the foregoing paragraphs where we explained the no arbitrage assumption. Thus, it is possible to derive the Black-Scholes model directly by using the no-arbitrage assumption combined with the perfect hedge assumption. But more important than that, the perfect hedge assumption leads to the concept of risk neutrality assumption which proves also to be a very useful and self-sufficient tool in order to explain and derive the Black-Scholes model.
It is commonly accepted that investors are risk averse - that they dislike bearing risk and will avoid risk unless compensated by a risk premium. In equilibrium, the risk premium manifests itself through the larger expected returns on risky assets relative to the riskless assets. If a certain asset does not provide a sufficiently large expected return to compensate for its risk, investors will sell the asset, thereby forcing down its price and increasing its expected return. Eventually, at a new, lower price the asset’s expected return will be adequate compensation for its risk and so induce risk averse investors to hold it in their portfolios.
In an economy where investors are risk averse, equilibrium pricing of risky assets requires finding the correct magnitude of the risk premium to satisfy all investors. ( e.g. CAPM, capital asset pricing theory, where E (rx ) = rf + b x ( E(rm) - rf ) rf = risk free rate, rx = return of risky asset x, rm = market rate of return, b x = a measure of the systematic risk of asset x, b x ( E(rm) - rf )=risk premium). In particular, investors will demand a risk premium before holding a risky common stock in their portfolios. The question is whether investors will also demand a risk premium for options. In a risk averse economy the answer is yes because options are typically more risky than common stocks. Hence the inducement to hold options should be greater than that for common stocks. In contrast, in a hypothetical economy where investors are risk neutral ( indifferent to risk ), all assets will return the risk free rate. In this hypothetical economy, there is no need to compensate investors for bearing risk.
Now, we can consider the concept of the riskless hedge. Since the perfect hedge, continuously adjusted, is riskless, there is no need to provide a risk premium for risk-averse investors to hold it. Thus, the riskless hedge, when viewed as a portfolio, will have the same value to risk neutral investors as to risk averse investors where the rate of return on the portfolio must be the risk free interest rate. Since the perfect hedge has the same value in both the risk averse and the risk neutral economy, it can be valued in the particular economy in which it is easiest to do. This is of course the risk neutral economy.
This idea is the risk neutrality argument. In short, given two economies identical in all respects except that one has risk-averse investors and the other has risk neutral investors, if it is possible to form a perfect hedge between the stock and associated options, then the options will have the same value in a risk neutral economy as in a risk averse economy. This follows because once we know that the stock price and the value of the perfect hedge portfolio is the same in both economies, then by elimination the option price must also be the same in both economies.
In a risk neutral economy, all assets have expected returns equal to the risk free rate. Hence,
E[ CT / Ct ] = e r(T-t) or Ct = E[ CT] e - r(T- t)
where CT = the option price at expiration time T, ST = stock price at time T
Ct = the option price at current time t , X = exercise price of the option
r = risk free interest rate
At expiration we know that CT = max ( 0, ST - X) , and we find that
Ct = e - r(T- t) E[ max ( 0, ST - X)]
Thus, by using the risk neutrality argument, the expected payoff of an option at its maturity date can be discounted at the risk free rate to determine the price of the option. To evaluate the expression E[ max ( 0, ST - X)] , one must also make use of the fact that in a risk neutral economy, the expected rate of return on a stock is the risk free interest rate as for all other assets. Thus,
E[ ST] = St e r(T-t)
One must emphasize that the risk neutrality argument does not actually require the stock price(or the price of the underlying asset) to increase at the risk free rate. Rather, it suggests that if a perfect hedge is possible, then investors can be assumed to be risk neutral and the option prices can be valued as if the stock price increases at the risk free rate.
4.1.3.The Derivation Of The Black - Scholes Model :
4.1.3.1. A Derivation Of The Black-Scholes Formula By Using The No-Arbitrage Argument
As suggested early, one way to derive the Black-Scholes formula for the value of a European call option on a stock is to combine shares of stock and call options so as to form a perfect hedge portfolio, or a portfolio whose value is insulated against changes in the value of the stock.
Let V
H = the value of the perfect hedge portfolio,S = the stock price
C = the price of the call option
n
S = the number of shares held in the perfect hedge portfolion
C = the number of call options held in the perfect hedge portfolioThe perfect hedge portfolio must satisfy the following two conditions:
VH = nS S + nC C
dVH = nS dS + nC dC = 0 (9)
These conditions are satisfied if, for every one share of stock we hold -1/ (¶ C / ¶ S) call options. Thus,
nS = 1 , nC = -1/ (¶ C / ¶ S) where ¶ C / ¶ S = D (delta of an option, hedge ratio)
As explained earlier, the model assumes that stock prices follow a Geometric Brownian motion where from (8) we know that percentage changes in stock prices follow a normal distribution
dS / S = (m + s 2 /2)dt + s sqrt(dt) z
Given the assumptions of the underlying stochastic process in ii.1), one can invoke Ito’s lemma, a fundamental result of stochastic calculus, which implies that we can express the changes in call option price as
dC = (¶ C / ¶ S)dS + (¶ C / ¶ t) dt + 0.5 (¶ 2C / ¶ S2 ) s 2 S2 dt (10)
The perfect hedge portfolio is free of risk. Hence, its percentage rate of return over any time interval must be the risk free interest rate times the length of the interval (no arbitrage argument), as follows:
dVH / VH = r dt (11)
Combining equations (9), (10), (11) and letting nS = 1 , nC = -1/ (¶ C / ¶ S), the change in the value of the perfect hedge portfolio can be written as
dVH = r dt VH = dS - (1/ (¶ C / ¶ S)) ((¶ C / ¶ S)dS + (¶ C / ¶ t) dt + 0.5 (¶ 2C / ¶ S2 ) s 2 S2 dt)
which in turn implies
¶ C / ¶ t = rVH (- ¶ C / ¶ S ) - 0.5(¶ 2C / ¶ S2 )s 2 S2 (12)
¶ C / ¶ t = -r S ( ¶ C / ¶ S ) + r C - 0.5(¶ 2C / ¶ S2 )s 2 S2
Using conventional differential equation solution techniques, one can solve this partial differential equation to find the option price using the boundary conditions that, if the stock price is zero the option value must be zero and at maturity the value of the option must be equal to
max(0,ST -X).
After solving the differential equation, the Black-Scholes formulas for the prices of European call and put options on nondividend paying stocks are as follows.
c = SN(d1 ) - Xe-rT N(d2 )
p = Xe-rT N(-d2 ) - S N(-d1 ) (From put-call parity relationship)
where
d1 = (In( S/X) + ( r + s 2 /2) T ) / s sqrt(T)
d2 = d1 - s sqrt(T)
c = the price of a European call option on a nondividend paying stock
p = the price of a European put option on a nondividend paying stock
S = the current stock price
X = the exercise price
T = time until expiration
s = standard deviation of logarithmic stock returns
r = risk free interest rate
N(.) = the cumulative probability function for a standardized normal variable
The Black-Scholes equations give the value of a European call or put option on a nondividend paying stock in terms of five variables: the current stock price, the exercise price, the risk free interest rate, the volatility and the time to expiration. The expected return on the underlying asset does not enter into the Black-Scholes equations. This follows implicitly from the risk neutrality argument. The Black-Scholes results can easily be extended to cover European call and put options on dividend-paying stocks and European options on stock indices as well as American call options on stocks and stock indices. We will deal with the application of the model to the ISE-30 and its extensions later in detail.
4.1.3.2. A Derivation Of The Black-Scholes Formula By Using The Risk Neutrality Argument
The risk neutrality argument was stated to be a powerful tool in the valuation of options as a consequence of the perfect hedge assumption. Thus, this argument suggests that, if a perfect hedge is possible between a stock and its option, then the option can be valued as if all investors in the economy are risk neutral. Hence, then the expected return from all securities is the risk free interest rate.
By using this argument and the assumption of geometric Brownian motion, it follows that
Ct = e - r(T- t) E[ max ( 0, ST - X)] and E[ ST] = St e r(T-t)
and from (6) E[ S(t + D t) | S(u), 0 £ u £ t ] = S(t) e (m + s 2 / 2) D t = S(t) e a D t
By the risk neutrality argument, the expected return on the stock is equal to the risk free interest rate.
Thus, T- t = D t ? r = m + s 2 / 2 = a (13)
Hence, a direct implication of the risk neutrality argument is that the geometric mean return on the stock is equal to the risk free rate. Further since { S(t), 0 £ t £ T } is a geometric Brownian motion process, we know that ( let t = 0, and S(t) = S0 and Ct = C0)
S(T) = S0 e Y(T) where Y(T) ~ N(m T, Ts 2 )
C0 e rT = E[ max ( 0, S(T) - X)]
C0 e rT
=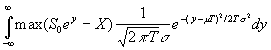
= 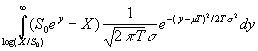
Let w = ![]()
![]() then
then
C0 e rT
= 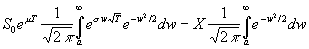
where a = 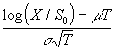
![]() =
= ![]()
![]()
= ![]() P
P![]() N(
N(![]() )
)
![]() =
= ![]()
![]()
where f is the standard normal distribution function.
Thus, C0e
rT = ![]() By risk neutrality, r = m + s 2 / 2
By risk neutrality, r = m + s 2 / 2
and let b = -a we get C0 = ![]()
where b = ![]()
Hence, by using the risk neutrality, one can easily derive the Black-Scholes model. In this derivation, the call option price is derived. By put-call parity relationship, one can directly find the put option price.
4.1.4. The Application Of The Black - Scholes Model On ISE-30 :
In our study, we applied the Black-Scholes option pricing model to the ISE-30 index option and the options on each of the 30 common stocks which comprise the ISE-30 index. The input data we used for the ISE-30 index consisted of 211 adjusted daily closing index level data between the period 01/02/1997 and 10/31/1997. Our analysis horizon begins from the date of the last data point 10/31/1997 when the ISE-30 index level closed the day at 3223 points. Thus, in all the pricing calculations, the current time is 10/31/1997 where t=0 and the current index level S0 = 3223. The next input variable of the model which also defines the underlying stochastic price process is the volatility s which is estimated as the standard deviation of the logarithmic daily returns of the index between the dates 01/02/1997 and 10/31/1997. Thus, relying on the assumption of the model that the volatility of the continuously compounded returns is constant, the future volatility of the returns during the life of the option is estimated from the historical volatility. The risk free interest rate which is also assumed to be constant by the model is taken as the average of the yearly returns of short-term government bonds which is 120%. This rate is equivalent to a continuously compounded return of 79%. The fourth input variable exercise price is a contract-specific variable which is determined by the stock exchange according to the spot market prices of the underlying assets of the options. In a given time, options with different exercise prices can be traded with all other variables the same. We assumed that different exercise price can exist with a step of 50, e.g. 4000, 4050, 3950 etc. The last input variable time until expiration is also a contract-specific variable. Generally, exchange-traded options have maturities of 1, 2, 3, 6 or 12 months. When applying the formula time related variables volatility and time until expiration are annualized. That is, the volatility per trading year is calculated as volatility per day times square root of 250 which is the number of trading days per year and the time until expiration is expressed in terms of years. But before one can apply the Black-Scholes model to the ISE-30, one has to make an adjustment to the price formulas of the model which is originally derived for stock options
In order to apply the Black-Scholes model to the ISE-30 index option, we use a simple rule that enables results produced for European options on a nondividend-paying stock to be extended so that they apply to European options on stocks paying a known continuos dividend yield. Since a stock index could be treated as a security paying a known continuous dividend yield, these adjusted Black-Scholes formulas can also be used to value European index options. Thus, ISE-30 stock index is analogous to a stock paying a continuous dividend yield. The dividend yield of ISE-30 is the weighted dividend yield of the stocks comprising the ISE-30 and it can be calculated if the dividend yields of stocks comprising the index are known.
To derive the adjusted price formulas for options on stocks paying a continuous dividend yield, we consider the difference between a stock that pays a continuous dividend yield at a rate q per year and a similar stock that pays no dividends. It is a fact that the payment of a dividend causes a stock price to drop by an amount equal to the dividend. The payment of a continuous dividend yield at rate q, therefore, causes the growth rate in the stock price to be less than it would otherwise be by an amount q. If, with a continuous dividend yield of q, the stock price grows from S today to ST at time T, then in the absence of dividends it would grow from Se-qT today to ST at time T. This argument shows that one gets the same probability distribution for the stock price at time T in each of the following cases:
Thus, when pricing a European option lasting for time T on a stock paying a known dividend yield at rate q, the current stock price is discounted from S to Se-qT to account for the reduction in the stock price due to the dividend yield and then the option can be valued as if the stock pays no dividends. By replacing S by S e-qT in the Black-Scholes formulas, we can obtain the price ,c , of a European index call option and the price ,p , of a European index put option where q is the continuous dividend yield rate. If the dividend yield rate is not constant during the life of the option , q is taken as the average annualized dividend yield during the life of the option. In our case, the historical average annual dividend yield for the ISE-30 index is declared as 11% by the ISE-bulletin.
The adjusted pricing formulas for a European index option are as follows:c = Se-qT N(d1 ) - Xe-rT N(d2 )
p = Xe-rT N(-d2 ) - Se-qT N(-d1 ) (From put-call parity relationship)
where
d1 = (In( Se-qT /X) + ( r + s 2 /2)T ) / s sqrt(T) = (In( S/X) + ( r - q + s 2 /2)T ) / s sqrt(T)
d2 = d1 - s sqrt(T)
c = the price of a European call option on a stock indexp = the price of a European put option on a stock index
S = the current value of the index
X = the exercise price
T = time until expiration
s = standard deviation of logarithmic index returns ( volatility of the index)
r = risk free interest rate
q = average annualized dividend yield on the index during the life of the option
N(.) = the cumulative probability function for a standardized normal variable
As suggested above, the dividend yield of ISE-30 is the weighted dividend yield of the stocks comprising the ISE-30 and it is calculated by the Istanbul Stock Exchange. In calculating q for option valuation purposes, only dividends where the ex-dividend date is during the life of the option should be included. Thus, the correct value for q is likely to depend on the life of the option. In ISE, dividend payments on individual stocks occurs seasonally (with a few exceptions, almost all of the ISE companies declare their ex-dividend dates(dividend payment dates) at a date within the last two weeks of May, but this fact may change in the future ) . Thus, in practice, when valuing options whose life horizons do not include the month of May, q can be taken zero. But for the sake of completeness and generality and in order to see the effect of the input of dividend yield on the option prices , in our study we took q first as 0.11 which is the average annual dividend yield of ISE-30. Then, we conducted sensitivity analysis to see the effect of changing the continuous dividend yield in a range between 0 and 0.5 on the prices of the ISE-30 options. Thus, we calculated the option prices for different values of q.
4.1.4.2. Sensitivity Analysis On The Input Variables Of The Black-Scholes Model
After having done the necessary adjustments to the theoretical foundation of the Black-Scholes model and gathered data for the input variables, we applied the Black-Scholes formulas to determine the prices for the European ISE-30 index option and European options on nondividend paying stocks comprising the ISE-30 index (See Table 4.1. for a particular realization). At this point, the question to ask was whether the results we obtained as the outputs of the Black-Scholes model were making any sense and whether they represented the trends and relationships between the inputs and the outputs of the Black-Scholes model correctly. In order to test this and understand the implications of the model in the Turkish capital markets, we considered for all input variables separately how option prices change when one of these input variables changes with all the others remaining fixed. Thus, for all 31 different options ( ISE-30 index option and 30 stock options) we conducted sensitivity analysis for each of the input variables of the Black -Scholes model:the current stock (index) price, the exercise price, the time to expiration, the volatility of the stock(index) returns, the risk free interest rate and the dividends expected during the life of the option.
The examination of the change in the model’s price arising from a change in the value of either a state variable or parameter is also known as comparative statics analysis and shows the sensitivity of the model to the inputs. The reader may refer to Figures 4.1, 4.2, 4.3 , 4.4 , 4.5 , 4.6 to see the results of the sensitivity analysis for the European call and put options on ISE-30 index. Next, the results of this analysis will be discussed in detail for the case of ISE-30.
4.1.5.Comparitive Statics Analysis
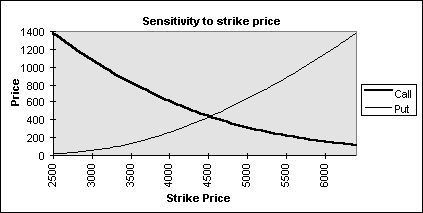
FIGURE 4.1.
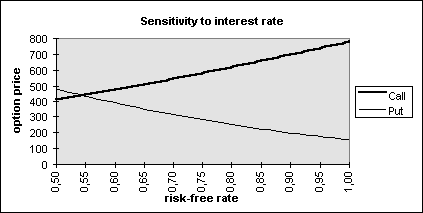
FIGURE 4.2.
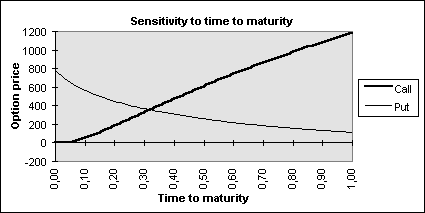
FIGURE 4.3.
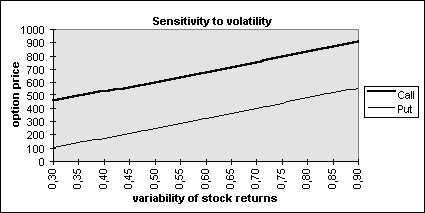
FIGURE 4.4.
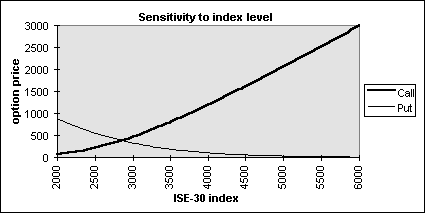
FIGURE 4.5.
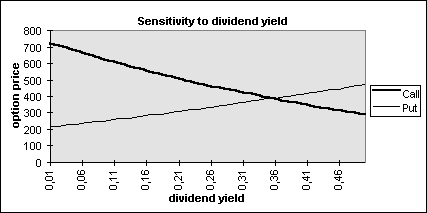
FIGURE 4.6.
A numerical example of option pricing on ISE-30 index option for a particular set of data:

TABLE 4.1
First, we consider the effect of the index level and the exercise price. These variables are the only two variables that have any influence on the value of the option at the expiration date when the option price consists of only its intrinsic value. If it is exercised, the payoff from a call option will be the amount by which the index level exceeds the exercise price. Call options, therefore, become more valuable as the index level increases and less valuable as the strike price increases. For a put option, the payoff on exercise is the amount by which the exercise price exceeds the index level. Put options, therefore, behave in the opposite way to call options. They become less valuable as the stock price increases and more valuable as the exercise price increases. As seen in Figure 4.1. and Figure 4.5., these arguments are justified by the results of the sensitivity analysis.
Next, let us consider the effect of the expiration date on the prices of European call and put options. Increasing the time to expiration decreases the present value of the exercise price paid on the expiration (if the option is exercised). Since the call option buyer pays this amount, and the put option buyer receives it, the effect of increasing time to expiration increases call option prices and decreases put option prices. In addition, increasing the time until maturity increases the likelihood of favorable outcomes for both puts and calls. Hence, as time to expiration increases, call option prices certainly increase. For American call and put options, the argument is different because of early exercise possibilities. Thus both American call and put options become more valuable as time to expiration increases as a result of increasing probability of favorable early exercise possibilities. In our study, the sensitivity analysis was conducted for European ISE-30 call and put options. As seen in Figure 4.3., the results for ISE-30 options are consistent with the arguments for European options.
The effect of a change in the risk free rate is similar to that of a change in time until expiration. Since increasing interest rates decrease the present value of the exercise price, one can certainly infer that there is a tendency for call option prices to increase and for put option values to decrease. In addition, as interest rates in the economy increase, the expected growth rate of the stock price tends to increase in the long run. This also causes to call option prices to increase and put option prices to decrease. The result of the sensitivity study is also consistent with these arguments as seen in Figure 4.2.
Another important variable related to the underlying stochastic process is the volatility which is defined as the standard deviation of continuously compounded index (stock) returns. As the volatility increases, the probability that the index will increase to very high levels or decrease to very low levels during the life of the option increases. For other investors who do not hold an option, these two outcomes will tend to offset each other. However, this is not the case for the owner of a call or put option. The owner of a call option benefits from price or index level increases but has limited downside risk in the event of price (index level) decreases, since the maximum loss is limited to the option price. Similarly, the owner of a put benefits from a decrease in the index level or price decreases but has limited downside risk if index level increases. Therefore, both call and option prices increase as volatility increases.
The last input variable to consider is the dividend yield of the index. In option pricing, a dividend is defined as the reduction in the stock price (index level) on the ex-dividend date arising from any dividends. Thus, the greater the dividends, the greater will be the reduction in the price of the underlying asset. Thus, the price of a call option decreases and the price of the put option increases as the amount of dividends during the life of the option increases. For the case of a stock index, the effect will be the same because as the continuous dividend yield q increases, the growth rate of the index decreases. The current level of index, S, will be discounted more since q increases. The result of the sensitivity study is also consistent with this argument as seen in Figure 4.6.
4.1.6. Adjustments For Dividends And American Options
In our study, our aim was to determine prices for all types of options at hand ( ISE-30 index options and options on stocks which comprise the ISE-30 index) no matter whether it is American or European or whether the underlying asset pays dividends or not. However, the original Black-Scholes model can only be used to value European call and put options on nondividend paying stocks. The basic structure of the Black-Scholes model was extended to price European index options. In this section, we will show how the basic Black-Scholes model is extended to cover European call and put options on dividend - paying stocks. Earlier, we had shown that American call options should never be exercised early when the underlying asset pays no dividends. This argument is important because it requires that an American call option on a nondividend paying stock must have the same price as a European call option on the same stock. But if the underlying stock pays dividends, early exercise of American call options becomes also a possibility. Nevertheless, we will show how we can price an American call option on a dividend paying stock if the amount and time of the dividend is known. Finally, we will state that the fact that early exercise of American put options may be desirable requires the price of an American put option to be always greater than the price of a European put option.
First, we consider European options on dividend paying stocks. At an ex-dividend date, the stock’s price goes down by an amount reflecting the dividend paid per share. The effect of this is to reduce the value of the calls and to increase the value of puts. European options on dividend paying stocks are analyzed by assuming that the stock price is the sum of two components: a riskless component that will be used to pay the known dividends during the life of the option and a risky component. The riskless component at any given time is the present value of all the dividends during the life of the option discounted from the ex-dividend dates to the present at the risk-free rate. The Black-Scholes formula is then correct if S is taken as the risky component. This means that the Black-Scholes formula can be used provided that the current stock price is reduced by the present value of all the dividends during the life of the option, the discounting being done from the ex-dividend dates at the risk-free rate.
The reader can refer to Table 4.2. to see a particular example for a European option on Akbank common stock. In this example, the current stock price is 12500 T.L., the exercise price is 19000 T.L. ,the stock price volatility is 66% per year, the continuously compounded risk-free rate is 79% and the time to maturity is 6 months. A dividend amount of 2000 T.L. per share is expected to be paid after 0.3 years. The present value of the dividend is subtracted from the current stock price of 12500 T.L. to find the riskless component. Then, this value is substituted for S in the Black-Scholes formula to find the option prices. As seen from the table, as a result of dividend payment the call price decreases and the put price increases relative to the case where no dividend is paid.