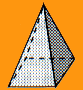Pirâmides
A figura mostra uma pirâmide. O ponto V é seu vértice e o polígono ABCDE, contido no plano a, é sua base. A altura da pirâmide é a distância h entre o ponto V e o plano a.
As faces triangulares que têm o vértice V em comum chamam-se faces laterais. O segmentos VA, VB, VC, etc. são as arestas laterais. Para as pirâmides, a relação entre a área total, a área lateral e a área da base é dada por:
St = Sl + Sb

Classificação das Pirâmides
a) Segundo o número de arestas da base:
Pirâmide Triangular: é aquela cuja base é um triângulo.

Pirâmide Quandrangular: é aquela cuja base é um quadrilátero.
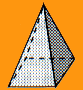
Pirâmide Pentagonal: é aquela cuja base é um pentagono.
E assim por diante ...
b) Segundo a forma da base:
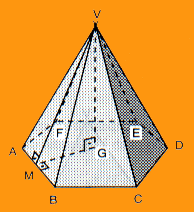
Pirâmide Regular: é a pirâmide cuja base é um polígono regular e na qual a projeção do vértice V sobre o plano da base é o centro G desse polígono. Na figura temos representada uma pirâmide hexagonal. Ali, temos:
VG = h = altura
GM = apótema da base
VM = apótema da pirâmide
Numa pirâmide regular, as faces laterais são trinângulos isósceles congruentes entre si.
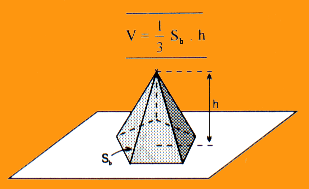
Volume de um Pirâmide
O volume de uma pirâmide qualquer é a terça parte do produto da área da sua base, pela sua altura.
Se Sb é a área da base e h é a altura, temos: