COORDINACIÓN DE GEOMETRÍA ANALÍTICA
SERIE No. "3" 2000-II
"LA RECTA Y EL PLANO"
1. Sea L la recta cuyas ecuaciones son:
![]()
Calcular:
a) La distancia del origen de coordenadas, a la recta L.
b) La distancia entre la recta L y el eje de las cotas.
c) Los ángulos ![]() que forma la recta L con los ejes coordenados X, Y y Z, respectivamente.
que forma la recta L con los ejes coordenados X, Y y Z, respectivamente.
2. Sean ![]() las rectas cuyas ecuaciones son:
las rectas cuyas ecuaciones son:
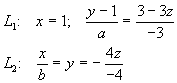
Si dichas rectas son perpendiculares entre sí, y además se intersecan, determinar los valores de "a" y "b".
3. Sean las rectas L y R definidas de la siguiente manera:
L: pasa por el origen, está contenida en el plano YZ, y forma un ángulo de ![]() con el eje Y.
con el eje Y.
R: es paralela al eje Z y corta al eje X en el punto P de coordenadas (2, 0, 0).
a) Determinar unas ecuaciones paramétricas de las rectas L y R.
b) Indicar si las rectas L y R definen un ángulo entre sí. En caso afirmativo, calcularlo; en caso contrario, justificar su respuesta.
4. Sean las rectas ![]() cuyas ecuaciones son:
cuyas ecuaciones son:

a) Determinar si ![]() son paralelas, si se cruzan o si se cortan.
son paralelas, si se cruzan o si se cortan.
b) En caso de que ![]() se corten, determinar el punto de intersección; en caso de que se crucen o sean paralelas, calcular la distancia entre ellas.
se corten, determinar el punto de intersección; en caso de que se crucen o sean paralelas, calcular la distancia entre ellas.
5. Determinar las coordenadas del punto de intersección entre la recta:

y la recta que pasa por los puntos (4, 6, 8) y (0, 6, 0).
6. Calcular la distancia entre la recta
![]()
y el eje de las abscisas.
7. Sea la recta R que pasa por el punto P(4, -1, 0), que es perpendicular al eje X, y cuyo vector director tiene como ángulos directores ![]() ; y sea la recta L, una de cuyas ecuaciones vectoriales es:
; y sea la recta L, una de cuyas ecuaciones vectoriales es:
![]()
Determinar los valores de
a y b, tales que las rectas R y L se intersequen perpendicularmente.8 . Sea la recta L que tiene por ecuaciones:
![]()
Determinar las coordenadas del punto de la recta que está más cerca del origen de coordenadas.
9. Determinar unas ecuaciones paramétricas de la recta L que es coincidente con el eje X.
10. Determinar unas ecuaciones paramétricas de la recta R, que pasa por el punto ![]() , y que corta perpendicularmente a la recta L que tiene por ecuaciones:
, y que corta perpendicularmente a la recta L que tiene por ecuaciones:
![]()
11. Sea la recta L, unas de cuyas ecuaciones paramétricas son:

Determinar las coordenadas del punto de la recta que está más cerca del origen de coordenadas
12. Calcular la distancia entre las rectas ![]() que tienen por ecuaciones:
que tienen por ecuaciones:

13. Sea la viga ![]() que tiene por extremos a los puntos A(1, 2, 3) y B(7, 6, 5). Si desde el punto C(4, 5, 10) cae en forma vertical un objeto, determinar si éste golpea a la viga. En caso afirmativo, determinar el punto de contacto; en caso negativo, calcular a qué distancia de la viga pasará el objeto.
que tiene por extremos a los puntos A(1, 2, 3) y B(7, 6, 5). Si desde el punto C(4, 5, 10) cae en forma vertical un objeto, determinar si éste golpea a la viga. En caso afirmativo, determinar el punto de contacto; en caso negativo, calcular a qué distancia de la viga pasará el objeto.
Nota: despreciar el ancho de la viga y el del objeto.
14. Sea la recta ![]() que contiene al punto A(4, 0, 4), que interseca a la recta
que contiene al punto A(4, 0, 4), que interseca a la recta ![]() y forma con ésta un ángulo de
y forma con ésta un ángulo de ![]() . Si las ecuaciones de la recta
. Si las ecuaciones de la recta ![]() son:
son:
![]()
Determinar las coordenadas de los puntos de intersección entre ![]() (hay dos soluciones).
(hay dos soluciones).
15. Sea la recta L que pasa por el punto A(2, 4, 6) y que forma ángulos agudos iguales con los ejes X y Y. Si el ángulo entre la recta L y el eje Z es de ![]() , determinar:
, determinar:
a) El ángulo que forma la recta L con los ejes X y Y;
b) Unas ecuaciones paramétricas de la recta L;
c) El punto en el cual la recta L se interseca con el plano XZ.
16. Sean las rectas:

a) Calcular el ángulo que forman ![]() .
.
b) Determinar la distancia entre ![]() .
.
.
17. Sean las rectas L y R que tienen por ecuaciones:
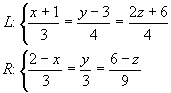
a) Si L y R se intersecan, determinar el punto de intersección; en caso contrario calcular la distancia entre dichas rectas.
b) Determinar el punto de intersección de la recta R con el plano XY.
18. Sean los planos:

Determinar:
a) La ecuación cartesiana del plano![]() que contiene al punto A(0, 7, -1) y que es simultáneamente perpendicular a los planos
que contiene al punto A(0, 7, -1) y que es simultáneamente perpendicular a los planos ![]() ;
;
b) Unas ecuaciones paramétricas de la recta R de intersección del plano ![]() con el plano YZ;
con el plano YZ;
c) El ángulo que forma el plano![]() con el eje Z.
con el eje Z.
19. Sean las rectas L y R que tienen por ecuaciones:

Determinar si las rectas L y R definen un plano. En caso afirmativo, obtener la ecuación cartesiana de dicho plano; en caso contrario, justificar su respuesta.
20. Determinar el punto de intersección entre los planos ![]() , cuyas ecuaciones son:
, cuyas ecuaciones son:

21. Determinar la ecuación cartesiana del plano que forman las rectas:

22. Determinar la ecuación cartesiana del plano que pasa por los puntos A(1, 0, -1) y B(2, 0, 2), y que forma un ángulo de ![]() con el plano de ecuación:
con el plano de ecuación: ![]()
23. Sea el plano![]() definido por los puntos A(3, 0, 0), B(0, 3, 0) y C(0, 0, 6).
definido por los puntos A(3, 0, 0), B(0, 3, 0) y C(0, 0, 6).
a) Calcular la distancia entre el punto Q(4, 2, 2) y el plano![]() .
.
b) Determinar el punto de intersección entre el plano![]() y la recta L que contiene al punto (-1, 1, 1) y que es normal al plano
y la recta L que contiene al punto (-1, 1, 1) y que es normal al plano![]() .
.
24. Determinar la ecuación cartesiana del plano![]() que es perpendicular al plano cuya ecuación es Y=0, y que contiene a la recta L de ecuaciones:
que es perpendicular al plano cuya ecuación es Y=0, y que contiene a la recta L de ecuaciones:
![]()
25. Sea el plano![]() cuya ecuación es
cuya ecuación es ![]() , y sea la recta L que tiene por ecuaciones:
, y sea la recta L que tiene por ecuaciones:
L: ![]()
Determinar, si existe, la intersección entre la recta y el plano.
26. Determinar la ecuación cartesiana del plano que contiene al punto P(2, -1, 4) y que es perpendicular a la recta L que tiene por ecuaciones:
![]()
27. Determinar la ecuación cartesiana del plano que pasa por el punto A(1, -2, 3) y que contiene al eje coordenado X.
28. Determinar las ecuaciones cartesianas de los tres planos que contienen a la recta L de ecuaciones:
![]()
y que son perpendiculares a los tres planos coordenados.
con el plano YZ.
30. Calcular el ángulo que forman la recta![]()
y el plano ![]()
31. Sean las rectas ![]() que se cruzan en el espacio, sin cortarse, y definido por:
que se cruzan en el espacio, sin cortarse, y definido por:

Determinar la ecuación cartesiana del plano![]() que contiene a
que contiene a ![]() , siendo ésta última ortogonal tanto a
, siendo ésta última ortogonal tanto a ![]() como a
como a ![]() .
.
32. Sean las rectas ![]() cuyas ecuaciones son:
cuyas ecuaciones son:
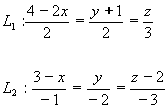
Determinar la ecuación cartesiana del plano![]() que contiene a
que contiene a ![]() .
.
33. Determinar las coordenadas del punto B que se muestra en la siguiente figura.
A(3,1,4)
90° B
p
: 2x -y +z -3 =0
34. Determinar la ecuación cartesiana del plano que es bisector del ángulo que forman las rectas L1 y L2 de ecuaciones:
![]()
![]()
35. Sea la recta L, unas de cuyas ecuaciones son:
![]()
y sea ![]() el plano cuya ecuación es:
el plano cuya ecuación es:
![]()
a) Calcular el ángulo que forma L con ![]() .
.
b) Determinar la intersección de L con ![]() , si ésta existe.
, si ésta existe.
36. Sea la recta L que pasa por el punto A(7, 0, 0) y que es normal al plano![]() de ecuación:
de ecuación:
![]()
a) Determinar el punto de intersección entre dicha recta y el plano.
b) Si T1 y T2 son las rectas de intersección del plano![]() con los planos coordenados XZ y YZ, respectivamente, calcular el ángulo comprendido entre T1 y T2.
con los planos coordenados XZ y YZ, respectivamente, calcular el ángulo comprendido entre T1 y T2.
c) Determinar unas ecuaciones en forma simétrica de la recta que pasa por el punto A y que es simultáneamente perpendicular a las rectas mencionadas en el inciso anterior.
37. Determinar la ecuación cartesiana del plano que contiene a la recta L y que es perpendicular al plano ![]() si:
si:

38. Sea el punto P(1,2,3) y sea la recta L:
L: x-2 = -y = 3-z
Determinar:
39. Sean la recta L y el plano p, cuyas ecuaciones son:
![]() p: 3x -2y +nz = 0
p: 3x -2y +nz = 0
Determinar los valores de "m" y "n" que hacen a la recta y el plano perpendiculares.
40. Obtener una ecuación vectorial de la recta L3 que interseca perpendicularmente a las rectas L1 y L2 de ecuaciones:

41. Obtener la ecuación cartesiana de un plano
p que es perpendicular a la recta representada por la ecuación
42. Sean el plano
p y la recta L representados por las ecuaciones:p: 3x + 6y +2z = 72
![]()
Determinar:
3. a) Si 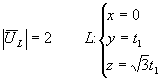 si
si  b)
b) ![]()
7. a = 17, b = -4
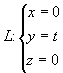
15. ![]()
17. a) Pint (-1, 3, -3) b) Pint (0, 2, 0)
19. 2x + 3y - 4z - 6 = 0
21. 6x + 4y - 3z - 24 = 0.
25. La intersección es L.
27. 3y + 2z = 0
29. 2x + y - 2z + 2 = 0
31. ![]()
33. B(1,2,3)
b) L es la intersección.
37. 17x - 18y - 5z + 39 = 0
39. m = -6, n =![]()
41. 2x-2y-z-18 = 0