COORDINACIÓN DE GEOMETRÍA ANALÍTICA

SERIE No. "4" 2000-II

 

"CURVAS"

 

1. Determinar una ecuación polar para cada una de las rectas horizontales que son tangentes a la circunferencia cuya ecuación polar es r = 3.

2. Sea la parábola C, una de cuyas ecuaciones vectoriales es:

Determinar:

a) unas ecuaciones cartesianas de dicha parábola;

b) las coordenadas cartesianas del vértice de la curva, y

c) para qué valor del parámetro t se obtienen las coordenadas del vértice.

3. Determinar si las ecuaciones paramétricas:

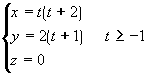
y la ecuación polar: representan el mismo lugar geométrico.

4. Determinar una ecuación polar para la circunferencia de radio igual a 4, que tiene como centro al punto de intersección entre las rectas L1 y L2. La recta L1 es perpendicular al eje polar y pasa por el punto. La recta L2 es paralela al eje polar y pasa por el punto

5. Sea la curva que tiene por ecuación polar:

Determinar:

a) sus intersecciones con el eje copolar;

b) si es simétrica con respecto al polo;

c) si es abierta o cerrada;

d) sus ecuaciones cartesianas; y

e) las coordenadas del punto que pertenece a la curva y que está más próximo al

origen de coordenadas.

Identificar la curva y trazar su gráfica.

6. Sea la curva C, una de cuyas ecuaciones vectoriales es:

Determinar unas ecuaciones paramétricas así como unas ecuaciones cartesianas de la curva. También, identificarla y trazar su gráfica.

7. Sea la curva C representada por la ecuación vectorial:

a) Determinar sus ecuaciones cartesianas.

b) Identificar la curva.

c) Trazar su gráfica.

8. Sean las curvas C1 y C2 que son representadas por las ecuaciones vectoriales:

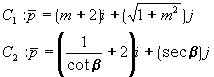
a) Determinar si C1 y C2 representan el mismo lugar geométrico.

b) Determinar una ecuación polar de la curva C1.

9. Sea la curva representada por la ecuación polar:

Determinar:

a) su intersecciones con los ejes polar y copolar.

b) si es simétrica respecto al eje polar y al eje copolar.

Trazar la gráfica e identificar la curva.

10. Sea la circunferencia que tiene por ecuación polar a:

a) Calcular su radio.

b) Determinar unas coordenadas polares de su centro.

11. Sea la curva de ecuación polar:

Determinar:

a) Sus intersecciones con los ejes polar y copolar.

b) Si es simétrica con respecto al eje copolar.

c) Si es abierta o cerrada.

Trazar la gráfica.

12. Sea la curva C, unas de cuyas ecuaciones paramétricas son:

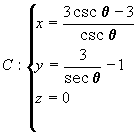
Determinar unas ecuaciones cartesianas de la curva. Identificarla y trazar su gráfica.

 
  1. Dada la curva de ecuación polar

determinar

  1. Si es simétrica respecto al eje polar.
  2. Todas sus intersecciones con los ejes polar y copolar.

 

14. Sea la curva de ecuación polar:

 

Determinar:

a) si es simétrica con respecto al eje polar;

b) las coordenadas polares del punto de la curva más alejado del polo ( dos

soluciones).

Trazar la gráfica.

 

15. Sea la curva de ecuación polar:

Determinar:

a) Intersecciones con los ejes.

b) Simetrías.

c) Si es abierta o cerrada.

d) Unas de sus ecuaciones cartesianas.

e) Los valores de r para

f) Trazar su gráfica.

 

16. Sea la circunferencia C, una de cuyas ecuaciones polares es:

Determinar:

a) el valor del radio, así como unas coordenadas polares del centro;

b) los puntos donde la circunferencia se interseca con el eje polar.

17. Determinar e identificar la ecuaciones cartesianas de las curvas:

a)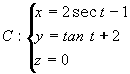

b)

c)

d)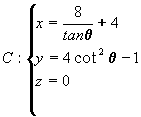

e)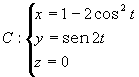

18. Sea la curva C, una de cuyas ecuaciones polares es:

Determinar:

a) si la curva pasa por el polo;

b) si es simétrica respecto al polo y al eje polar;

c) sus ecuaciones cartesianas.

19. Sea la curva C, una de cuyas ecuaciones polares es:

Determinar:

a) sus puntos de intersección con los ejes polar y copolar;

b) si es simétrica respecto al polo;

c) sus ecuaciones cartesianas.
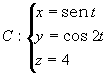
  1. Determinar las ecuaciones cartesianas de la curva representada por las ecuaciones paramétricas:

21. Sea la curva C, una de cuyas ecuaciones vectoriales es:

Determinar:

a) sus intersecciones con los ejes coordenados X y Y;

b) una ecuación polar de la curva.

Resultados de los ejercicios impares.

1.

 

3. No representan el mismo lugar geométrico.

 

5. a) no tiene, b) sí es simétrica, c) es abierta, d) xy = 2,

e)

 

7. a)

b) Circunferencia de centro (3, 3, -2), radio = 4.

 

9. a) intersecciones con el eje polar: no hay; intersecciones con el eje copolar:.

b) simetría con respecto al eje polar: no hay; simetría con respecto al eje copolar: si hay.

La curva es una rosa de tres pétalos.

 

11. a)

  1. b) Si es simétrica.

c) La curva es abierta.

13. a) No es simétrica respecto al eje polar

b) 5 puntos de intersección A(10,0), B(10,p ), C(25,p /2), D (5,p /2) y E(0,0).

 

 

15. a) Intersecciones con el eje polar:

Intersecciones con el eje copolar:

b) Simetría con el eje polar: si existe.

Simetría con el eje copolar: no existe.

c) La curva es cerrada.

d) , z = 0

 

e) Los valores de r son: 3, 1.95, 0.375, 0, -0.375, -1.95 y -3.

 

17. a) Hipérbola.

b) Circunferencia (mitad superior).

c) Hipérbola (rama derecha).

d) Parábola.

e) Circunferencia.

 

19. a) Eje polar: Eje copolar:

b) No hay simetría.

c) , z = 0

 

21. a) Eje X: A(0,0), B(2,0) Eje Y: A(0,0), C(0,-2)

b)