COORDINACIÓN DE GEOMETRÍA ANALÍTICA

Regresar

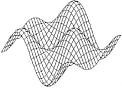
SERIE No. "5" 2000-II

"SUPERFICIES"

 

  1. Determinar la ecuación de la superficie de revolución (hiperboloide de dos mantos) que se forma al girar la curva:

alrededor del eje "".

 

 

  1. Determinar la ecuación del cilindro que contiene a la curva de ecuaciones:

y cuya generatriz es perpendicular al plano:

 

 

  1. Obtener la ecuación cartesiana de la superficie que tiene por generatriz y directriz respectivamente a las curvas:

    2.  

  2. Sea la superficie cuadrática

.

Determinar:

  1. sus trazas con los planos "" y "";

  2. su simetría respecto al origen;

  3. la extensión de la curva en la dirección de "

".

5. Determinar la ecuación de un toroide que se forma al girar una circunferencia de radio 2 unidades, tangente al eje "" en el punto y que pasa por el punto ; alrededor del eje "".

 

 

  1. Dada la ecuación del hiperboloide de dos mantos:

    2. Determinar la distancia entre sus vértices.

     

     

  2. Sea la superficie cuya ecuación cartesiana es:

Determinar:

  1. las trazas con respecto a los planos coordenados;

  2. su simetría respecto al origen.

Identificar la superficie.

 

 

  1. Obtener la ecuación cartesiana de la superficie de revolución que se genera al girar la curva de ecuación polar , alrededor del eje copolar.

    2.  

  2. Sea la superficie cuya ecuación cartesiana es Determinar su extensión en la dirección de los ejes coordenados e identificarla.

    3.  

  3. Obtener la ecuación cartesiana de la superficie que se genera al girar la curva:

    4. alrededor del eje Z.

    Identificar la superficie.

     

     

  4. Escribir en los paréntesis las letras que completen correctamente las siguientes proposiciones:

Sea

a) Si A=B=C=D0, la ecuación representa ( )

1. un cono. 2. un hiperboloide de un manto.

3. un elipsoide 4. un paraboloide elíptico.

b) Si A>0, B>0, C<0, y D>0, la ecuación representa ( )

1. un elipsoide. 2. un hiperboloide de un manto

3. un cono 4. un hiperboloide de dos mantos.

c) Si A>0, B>0 y C=D=0, la ecuación representa ( )

1. un paraboloide de revolución. 2. un punto.

3. un plano. 4. una recta.

d) Si A>0, B>0, C<0 y D=0, la ecuación representa ( )

1. un hiperboloide de dos mantos. 2. un cono.

3. un hiperboloide de un manto. 4. una esfera.

  1. Si A>0, B>0, C>0 y D=0, la ecuación representa

1. una esfera 2. un punto

3. un plano 4. una recta.

12. Sea la superficie S, una de cuyas ecuaciones vectoriales es:

Determinar la ecuación cartesiana de la superficie e identificarla.

  1. Sea el punto de intersección de las rectas y

dadas por:

Utilizar el método de las generatrices para determinar la ecuación cartesiana del plano que contiene a las rectas y (considerar al plano como una superficie cilíndrica).

14. Determinar la ecuación cartesiana de la superficie que se genera al girar la curva

Alrededor del eje . Identificar la superficie.

 

15. Mediante el método de las generatrices, determinar la ecuación cartesiana de la superficie que tiene por generatriz a la curva ,una de sus directrices es la curva , y la otra directriz es una recta contenida en el plano , pasa por el origen y forma 45º con los ejes y .

 

16. Determinar la ecuación cartesiana de la superficie cuya generatriz y directriz son, respectivamente, las curvas y que tienen por ecuaciones:

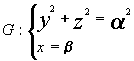
Esbozar la gráfica de la superficie e identificarla.

 

17. Determinar la ecuación cartesiana de la superficie:

Determinar

  1. su traza en el plano ,

  2. su simetría con respecto a los ejes y

, y

su extensión en la dirección del eje

 

18. Sea la recta perteneciente a la familia de rectas paralelas entre sí que forman la generatriz de una superficie, y sea la curva:

una de las trazas de la superficie. Determinar la ecuación cartesiana de la superficie e identificarla.

 

 

19. Determinar la ecuación vectorial para el cono circular recto que tiene su vértice en el punto y cuya traza con el plano es la curva C que tiene por ecuaciones:

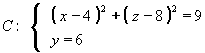
20. Sea la superficie cuya ecuación es: .

Determinar:

    1. Sus trazas con los planos paralelos a los planos coordenados.

    2. Su extensión en dirección de los ejes coordenados.

Identificar la superficie.

RESOLUCIÓN DE LOS EJERCICIOS.

  1. Es una superficie de revolución:

 

  1. Si la generatriz es perpendicular al plano dado, la normal de éste es el vector director requerido.

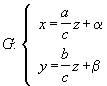
de las ecuaciones de la generatriz :

 

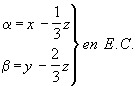
3.

      1. en (1)

      1. y (5) en (4)

      1. y (2) en E.C.

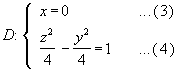
4.

–Traza

; 2 rectas paralelas.

- Traza

; 2 rectas paralelas

b)

x por –x, y por –y, z por –z

si es simétrica respecto al origen.

c) Cilindro circular recto, eje coincidente con "Z", por lo tanto:

5.

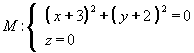
6.

Trazas XY y YZ.

Z=0 Hipérbola eje en y, centro en el origen.

X=0 Hipérbola eje en y, centro en el origen.

Intersecciones con el eje "y"

7.

  1. Trazas:

    2. "xy" z =0

    Eje transverso coincidente con "y"

    "xz" y =0

    Eje transverso coincidente con "z"

    "yz" x =0

  2. Simetría con respecto al origen: x por –x, y por –y, z por –z.

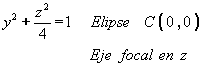
Si es simétrica respecto al origen.

Hiperboloide de un manto, de secciones elípticas y eje en "x".

8.

parábola V(0,0) abre hacia "y" positivo.

Paraboloide de revolución, vértice en el origen, eje coincidente con "y".

9.

Trazas:

""

Hipérbola C(0,0) eje transverso en "x"

""

Hipérbola C(0,0) eje transverso en "x"

""

no existe lugar geométrico en "yz". Pero si en la ecuación original

.Dos circunferencias punto en x=2 y x=-2

Hiperboloide circular de 2 mantos centro en el origen, vértices en: (2,0,0) y

(-2,0,0). Eje coincidente con x.

10.

  1. en (3)

  1. en (2)

(6) en (5)

(3) y (4) en E.C.

Hiperboloide circular de un manto c(0,0,0) y eje coincidente con el eje z.

11.

a) (3) d) (2)

b) (2) e) (2)

  1. (4)

12.

 

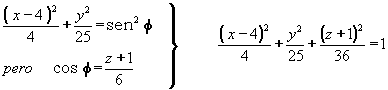
Es un elipsoide con centro c(4, 0, -1) y eje mayor paralelo al Z.

13.

Despejando x de (3) y sustituyendo en (1):

Despejando z de (4) y sustituyendo en (2):

Igualando (I) y (II):

Sustituyendo (1) y (2) en (E.C.):

 

14.

 

 

(c) y (d) en (E.C.)

Elipsoide circular (eje mayor sobre Y)

15.

De G y D1 De G y D2

(4) en (A) De (6) y (2)

en (B)

 

2 Y E.C.2

(C) en (1)

De E.C.1 Y (C)

(E) en (D)

16.

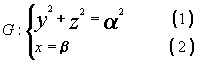
(4) en (1)

      1. y (2) en (3)

(1) y (2) en E.C.

Cono circular recto, vértice en el origen eje coincidente con X.

17.

circunferencia, centro en el origen, radio igual a uno.

b)

i) "y" x por –x y z por –z

; no hay simetría respecto al eje X.

ii) "z" x por –x y y por –y

; no hay simetría respecto al eje Z.

c)

18.

Vector director de L:

directriz la curva C, que tiene forma paramétrica

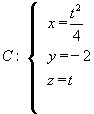
y en forma cartesiana:

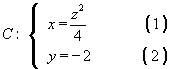
la generatriz:

(2) en (3) y (4):

en (1):

de (3) y (4)

en (E.C.)

o bien:

es un cilindro parabólico.

 

19.

Una solución es:

comprobación:

  1. en (ii):

20.

elipsoide de revolución

a)

elipses

 

 

circunferencias

 

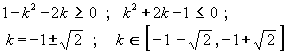
elipses

b)

1