Бен-Ицхак (19.12.2001) : ПЕРВЫЙ ВОПРОС: Во всех справочниках, учебниках, энциклопедиях написано, что ускорение земного притяжения g зависит от широты. На широте Москвы - одно значение, на полюсах - другое, и на экваторе - третье, причём - минимальное. Поэтому и космодромы стараются строить как можно ближе к экватору.
Я утверждал, и на этой ветке это зарегистрировано, что на самом деле здесь речь идёт не чисто только о g как неотъемлемом и постоянном гравитационном свойстве Земли, что здесь имеется ввиду разность собственно ускорения земного тяготения и противоположно направленной составляющей ускорения от действия центробежной силы за счёт вращения Земли. То есть: g'=g-w, и когда во всех справочниках говорят об изменениях g в зависимости от широты, имеется ввиду именно эта разность g'. На экваторе, где линейная скорость точки поверхности Земли равна 1668 км/ч или 463 м/сек, это ускорение от центробежной силы максимально, и его вектор w направлен в противоположную сторону от вектора ускорения земного тяготения g. На полюсах (истиных, конечно, через которые проходит ось вращния Земли) центробежная сила равна нулю, w=0, а g=g'.
Согласны вы с этим, а если у вас имеется альтернативная версия того, почему ускорение земного тяготения принимается на различных широтах различным, изложите её, пожалуйста.
Ответ.
В вышеприведенном рассуждении и во всех ваших предыдущих рассуждениях имеет место терминологическая путаница.
Понятие о центробежной и центростремительной силе в ТОЧНОМ смысле этоих терминов относится только механической системе С ЖЕСТКОЙ СВЯЗЬЮ. Действительно, если у вас есть камень, вращающийся на веревочке около центра (руки, например), то между рукой и рамнем имеется связь, НИТЬ, веревочка. Смотри рисунок:
В такой системе сила “А” называется центробежной силой, а сила “В” – центростремительной. Обе эти силы приложены К НИТИ, и только потому, что они приложены к нити, эта нить находится в натянутом состоянии.
Пояснение (по поводу терминологии
) – сила “А” называется центробежной потому, что она стремится удалить от центра вращения дальний конец НИТИ (самой нити, а не то, что к ней привязано). Сила “В” называется центростремительной потому, что она приложена в направлении к центру вращения.Напомню, что ВСЕ законы Ньютона применимы и приложимы к
реальным телам ПРИ УСЛОВИИ, что массы этих тел не распределены в пространстве, а сосредоточены в одной точке – центре массы тела. Это надо постоянно иметь в виду и это, бывает, вызывает непонимание.
Теперь
НО В ТОЧКЕ КРЕПЛЕНИЯ (!!!) камня к нити действительно действуют ДВЕ силы, как вы и говорите
– “А” и “С”, взаимно уравновешивающие друг друга. Вследствие этого камень НЕ БУДЕТ перемещаться в радиальном направлении, но НИТЬ будет испытывать усилие растяжения. ВНИМАНИЕ!!! НЕ К КАМНЮ приложены эти две силы, а К УСЛОВНОЙ ТОЧКЕ КРЕПЛЕНИЯ - к ИДЕАЛЬНОЙ ТОЧКЕ, в которой нить и камень соединяются вместе!!! Проблема в том, что из таким образом нарисованной картинки МОЖНО СДЕЛАТЬ НЕВЕРНЫЙ ВЫВОД, что обе силы приложены к камню. Именно этот вывод вы и делаете.Физика рассуждает так:
Представим камень в виде точки с его массой. Проведем касательную (плоскость, линию, неважно
). Тогда на нить будет действовать сила “А”, а на точку-камень сила “С”.Вроде бы силы уравновешиваются. Но ЕДИНСТВЕННЫМ следствием этого является то, что точка-камень не перемещается в радиальном направлении. Из этого нельзя делать вывода, что на камень действует нулевая сила. Эти силы приложены к разным телам (одна к камню, другая к веревке). Но, поскольку они жестко связаны, то в точке их связи они равны, и
не более того.Поясним сказанное другим примером.
Камень просто висит на веревке, прикрепленной к потолку.
На камень действует сила притяжения со стороны Земли, его вес (черная стрелка). Неважно сейчас, что это тяготение, может даже человек взяться за камень, и натянуть веревку с во много раз большей силой.
Со стороны камня на веревку действует сила натяжения. Но и со стороны веревки на камень действует сила (называемая в механике “сила реакции опоры”, только для ясности) – красная стрелка. Силы уравновешиваются в точке крепления. Но нельзя сказать, что в этой точке равнодействующая сил равна нулю. Эти силы приложены к разным телам (!). А говорить, что равнодействующая сил равна нулю правомерно только в случае, если все силы, о которых идет речь, приложены к одному телу.
Не перемещается же наш камень не потому, что сумма всех сил, действующих на него (равнодействующая) равна нулю, а потому, что налицо ЖЕСТКАЯ СВЯЗЬ С ОПОРОЙ. Так, в любой конструкции на ее отдельные элементы могут действовать разнообразные силы. И конструкция находится в покое до тех пор, пока эти силы не превышают внутренних сил сопростивления материала. Но разве можно сказать, что на консоль с подвешенным к ней грузом не действует никакая сила только потому. что вся конструкция находится в покое? Любому конструктору очевидно, что так сказать и так считать нельзя.
Снова переходим случаю вращения камня на веревке вокруг некоего центра.
Это
“
Тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока какая-то сила не выведет его из этого состояния”.Причина, вызывающая возникновение всех трех сил
– НЕВИДИМАЯ. Никто “физический” за камень не тащит в радиальном направлении. Эта сила возникает САМА, как следствие ДВИЖЕНИЯ камня с определенной скоростью. Сегодня НИКТО на Земле не знает ПРИЧИНЫ возникновения силы инерции и вообще ЧТО ТАКОЕ ИНЕРЦИЯ. Дело абсолютно темное. А школьникам объясняют по-простому, что вот, “закон такой”. А рассчитывается так-то. И начинают решать массу задач на вращательное движение, обойдя молчанием ПРИЧИНУ возникновения радиальной силы в данном случае. Что же нам остается делать? Да то же самое. Мы не умнее папы, поэтому делаем то, что он сказал – смотри вышеизложенное.Теперь выходим в космос
, но будем рассуждать несколько иначе, чтобы не повторяться:Пусть некое тело движется в космосе с некоторой скоростью
V. До тех пор, пока на него не действует никакая сила, оно продолжает так двигаться. Теперь представим себе (для простоты, конечно), что оно пролетало мимо какой-то очень большой массы.
Но, для простоты
предположим, что тяготение этой “Массы” как бы “включилось” в точке “А”. Ясно, что после этого, на движущееся тело начнет действовать сила, и в полном соответствии с вышеуказанным законом Ньютона пролетающее тело начнет отклоняться от направления прямолинейного движения, все время двигаясь в направлении, указанном стрелкой.Это направление всегда направлено точно на центр “Массы”. И, в зависимости от силы притяжения со стороны этой массы, траектория движения нашего тела будет более или менее криволинейной.
Заметим, что НИКАКОЙ ДРУГОЙ СИЛЫ на наше летящее тело не действует.
И в дальнейшем
– тоже не будет никаких других сил, только эта. (Собственно с этого наш спор и начался).При одном условии криволинейная траектория может превратиться в круговую:
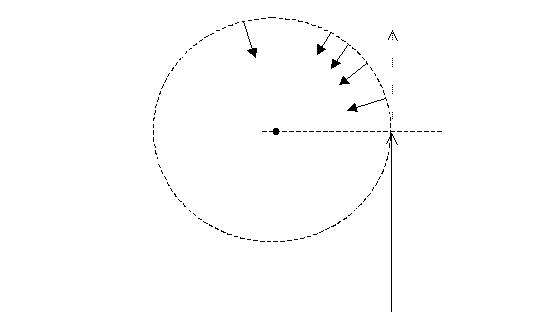
Для этого нужно, чтобы сила притяжения со стороны “Массы” была такой, чтобы в каждый следующий отрезок времени в любой точке эта сила уводила наше летящее тело от направления прямолинейного движения (относительно этой же мгновенной точки) на такую величину, чтобы оно снова оказалось на круговой траектории. Все. Тело стало спутником “Массы
”.Примечание: Я специально
“включил притяжение” в момент “А”, в точке “А”. Потому что если рассматривать вхождение летящего тела в поле тяготения, то задача сильно усложняется, и траектория обязательно будет эллиптической.Таким образом, мы подошли к решению нашей задачи не со стороны Земли, не с помощью разгоняющегося автомобильчика, а из космоса. И мы получили совершенно правильное решение задачи, а именно:
Мы видим, что при движении тела в космосе по круговой орбите, на него действительно действует ТОЛЬКО ОДНА СИЛА – сила притяжения со стороны “Массы” (Земля, звезда, Солнце – неважно). Само же движение происходит из-за движения нашего тела по инерции.
Но! Движение нашего тела по инерции происходит
“равномерно”. Во время этого движения никакая сила не действует, поэтому нет ни ускорения, ни замедления; скорость постоянна.Но в радиальном направлении сила ДЕЙСТВУЕТ. И действует она все время
, постоянно, иначе орбита не может быть круговой.А согласно второму закону того же Ньютона, если на тело действует сила, то оно начинает двигаться с ускорением
(F=ma). Отсюда следует, что в направлении действия этой силы на самом деле происходит движение (иначе быть не может) и это движение – равноускоренное.(Другой вопрос. Чему это ускорение равно, сейчас это нас не интересует. На разных орбитах у разных тел оно разное, и легко вычисляется. Так, для геостационарного спутника на высоте 40 тысяч км это ускорение вовсе не 9,8 м
\сек квадрат, а раза в три меньше).Поэтому мы имеем право сказать. что спутник на круговой орбите все время падает на землю, но вследствие того, что из-за движения по инерции он все время стремится уйти подальше, он остается на круговой орбите.
(Эллиптических орбит не рассматриваем ввиду сложности вопроса.)
Из всего этого должно быть ясно, что случай с камнем на веревке
, и случай со спутником на орбите – два принципиально разные случая. В первом имеется жесткая связь, поэтому возникают ТРИ силы – А,В,С.Во втором случае для кругового движения достаточно всего одной силы.
(Конечно, есть и сила “В”, действующая со стороны спутника на земной шар, но она пренебрежимо мала. Но никакая сила “А”, которую вы называете центробежной, на спутник не действует).
Вы же эти два случая считаете одним и тем же случаем
. Я постарался показать, что это неправомерно. Это первая ошибка. Вторая ошибка, вытекающая из этой – утверждение, что на спутник действуют какие-то другие силы кроме указанной одной.Само утверждение, что при движении спутника притяжение уравновешивается какой-то другой силой (независимо от ее названия) приводит к тому, что их равнодействующая должна быть равна нулю (ведь они приложены к одному телу!). А раз это так, остается только движение по инерции, и нет причин для движения тела-точки по кругу. Оно должно улететь в пространство. А этого как раз и
не происходит в силу указанных выше причин. Единственная сила (притяжение) переводит прямолинейное движение в круговое.ОТВЕТ НА ВОПРОСЫ:
После всего этого можно перейти к ответам на ваши вопросы:
ПЕРВЫЙ ВОПРОС: Во всех справочниках, учебниках, энциклопедиях написано, что ускорение земного притяжения g зависит от широты. На широте Москвы - одно значение, на полюсах - другое, и на экваторе - третье, причём - минимальное. И вы считаете, что по ЭТОЙ причине космодромы стараются строить как можно ближе к экватору.
…Так вот - в справочниках написана сущая правда. Но ваш вывод
– неверен, потому что основан на вашем неверном представлении о действии сил на предметы.Действительно, суммарное ускорение силы тяжести зависит от широты. Но
, если вы воспользуетесь цифрами, приведенными вами же, то увидите, что величины “g” на полюсе и экваторе отличаются всего на 0,5% !! Это вовсе не та причина, по которой космодромы стараются строить поближе к экватору. На самом деле причина другая, которая содержится в ваших же цифрах. А именно:Для вывода спутника на орбиту ему нужно придать определенную скорость. Для вывода спутника на круговую орбиту недостаточно
“выстрелить тело под определенным углом к горизонту; оно выйдет на эллипотическую, а не на круговую орбиту. Поэтому спутник вначале выводят на эллиптическую орбиту (на элемент эллиптической орбиты, и не дожидаются, пока он станет по ней крутиться), а через небольшое время, когда он уже высоко над землей, и находится примерно на высоте нужной круговой орбиты, разворачивают корабль в нужном направлении, включают последнюю ступень и доводят скорость до первой космической. Но на первом этапе (эллипс) скорость, до которой нужно разогнать объект, значительно ниже первой, она равна (приблизительно) 5 км\сек. И вот тут-то и проявляется преимущество экваториальных космодромов – тело, находящееся на земле, УЖЕ двигается со скоростью 500м\сек. Это – не полпроцента, это весомые 10% от необходимой скорости. Вот ради этих 10% и стоило стараться на первых этапах развития космонавтики строить космодромы ближе к экватору.А когда мощности ракет стали уже избыточными, когда выяснилось (смешно, но факт), что
расчетная полезная нагрузка бывает несколько больше реальной, то даже начали добавлять балласт! На орбиту выводят мешки с песком! А впоследствии стали брать на борт дополнительные малые спутники, отстреливая их по дороге.И, наконец, появилась возможность строить космодромы в более удобных с некоторых точек зрения местах, например Плесецк
– практически у полярного круга.Это все, что я имею сказать по данному вопросу. Это не моя “альтернативная” точка зрения, как вы выражаетесь. Именно так рассчитываются орбиты, именно такой подход (единственно верный) имеет место быть у специалистов по небесной механике. И если бы я позволил себе думать “альтернативно”, как Вы мне это однажды предложили, то потерял бы работу уже давно, еще будучи в России.
(Возможно, тут где-то есть мелкие неточности, но не по существу дела). Кстати, на следующем рисунке приведена картинка из классического учебника физики. На ней можно видеть. что на тело, вращающееся в коспосе вокруг большой массы, действует только одна сила - сила притяжения со стороны этой большой массы.
