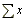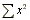Data Evaluation

Here are a few things you might want to know how to do--it looks really good under the Sample Calculations portion of a lab, since teachers here basically expect you to use your calcuator!

mean (average)
deviation (error)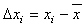
mean deviation
variance
standard deviation
percent error

Mean: Mean is basically the fundamental thingie of statistics. To compare numbers you need to know how different those numbers are from some starting point. Ideally you would want a starting point that is comparable to the values you measure. Thus the mean is born.
The mean is simply the arithmetical average of a few values. It's important to make sure the data you average is measuring the same thing!
Deviation: Deviation is simply a measure of how far any one value in a data set is from the average of the data set (some people will call this precision). Deviation by itself isn't important, but it is useful in other statistical measures. An interesting fact is that the algebraic sum (meaning keep up with the positive and negative values) of all the deviations is zero. This is in fact just another way of saying that half the people in your class are above the class average. If all of the deviations are small then at least you were consistent with your measurement technique.
Mean Deviation: Obviously from the discussion above it makes perfect sense that if you average the deviations you should get zero. As a consequence mean deviation requires a third, hidden, step-lose the signs on the numbers. To get the mean deviation simply sum the absolute value of all the deviations and then divide by the number of values you added together. This statistic gives you an idea of how good the experiment was performed. If the mean deviation is small then your numbers are going to be grouped pretty close together.
Standard Deviation & Variance: So we have all these numbers that tell us how good we are at measuring things in the lab. We also can tell sort of how close our measurements are to the average. Variance and standard deviation get into the idea of how closely the measurements group together. For example if your measurements are grouped wildly, as would occur if the variance were high, then there may be something wrong with the lab equipment. If, on the other hand, the variance of the measurements is low and the result does not match what you should have gotten, then there is probably something wrong with your procedure.
Standard deviation is more of a tool used to predict how well a piece of equipment measures. It is most useful on extremely large data sets. Perhaps you have heard of the dreaded scourge of college known as the "BELL CURVE." This is simply a fact of life. If you make a measurement, most of the values will be close to the average; the farther a value is away from the average the less likely it is to occur. For example if you look around a classroom you will probably see several 5'4'' girls, you might see a 5'11'' girl but chances are that you won't see a 7' girl. The further away a measurement is away from the average the less likely it is to occur. In this example standard deviation would be about 6''. Thus by the time you get 3 standard deviations, or 18'', away from the average (5'4'') or to a height of about 6'10'' you will almost never see a girl this tall.
% Error: So we are now able to understand all of these great tools that allow us to compare the numbers we measured in the lab to themselves. For example, I now know the average of all the values that I measured, but how does this value compare to the value that I know to be correct. This is where percent error comes in. Percent error is a value that describes how close the value I measured is to the value that is accepted as being correct. Notice the difference on top of the equation is a measure of how far the measurement is away from the accepted, or heoretical, value. This difference is then scaled according to the accepted value.
The reason percent error is so handy is exemplified in the following example. If I measure the distance from Hooper to the dorm and tell you I am off from the accepted value by only 30 meters, have I done a good or bad job of measuring. If on the other hand I measure the distance from Hooper to Jackson, MS and indicate that I am off from the accepted value by only 30 meters, have I done a better job or a worse job. Percent error helps to quantify how close your measurement is to the accepted value.
Math Symbols:: The math symbols in the equations are shorthand forms. These shorthand forms allow you show a lot of information in a little bit of space. To accomplish this little test look at the following data table. Print this out and impress your teacher (okay, maybe not...)

	average
	sum of values
	sum of (values)²
S_x	a weird calculation of standard deviation
_x	standard deviation
n	number of values