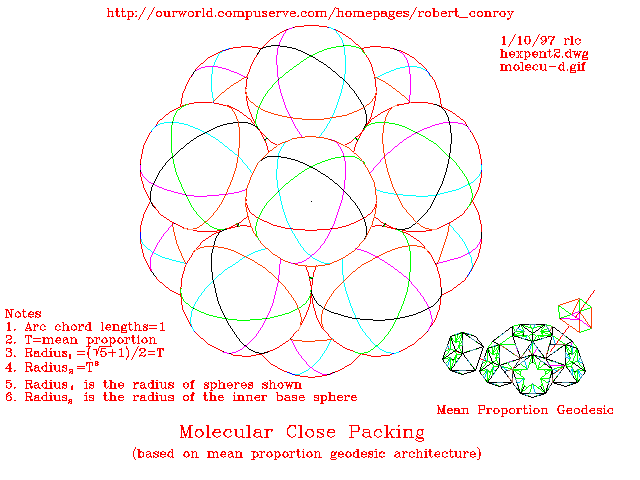
The following drawing represents the golden section close packing of molecules. It is presented as 12 sphericals each having 6 individual orbits per sphere. The structure of each sphere is along the lines of a icosidodecahedron encased in the space structure of a truncated icosahedron. Based on the arc segment chord lengths of the icosidodecahedron being unity, the outer 12 encased icosidodecahedrons sphericals have a radius of Tau ((square root of 5) + 1)/2) and the inner icosidodecahedron encased in a space frame dodecahedron has a radius of Tau (squared). The outer orbits touch but do not overlap at any place. The inner icosidodecahedron spherical is not evident in this diagram but its surface is penetrated by the outer spheres in the form of 12 pentagon shaped dimples of a chord length of Tau. The individual 6 orbits of the inner and outer spheres are not in conflict. This is a work in progress. Feel free to add comments. updated 2/25/97 rlc. Reworked on 2/19/98 rlc.
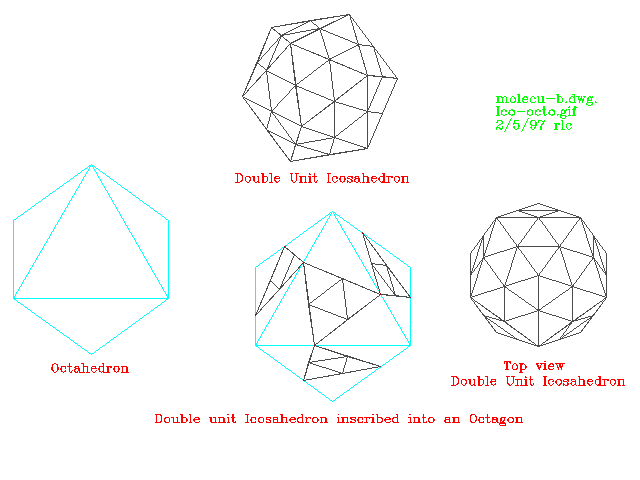
The following graphic is of a double unit icosahedron inscribed into an octahedron.
The following graphic is of a double unit icosahedron inscribed into a tetrahedron. This double unit Icosahedron would be 1/2 the the size of the one inscribed into a octahedron with an equivalent chord length. Actually 4 more 1/4 sized double unit icosahedrons could be inscribed into this same tetrahedron, but for simplicity, they are left out in this graphic.

By combining icosidodecahedrons inscribed in octahedrons to those of icosidodecahedrons inscribed into tetrahedrons would give you an octet type of packing arrangement. This can be considered a double enclosed 3 dimensional fractal because not only can the octet be built into larger octahedrons and tetrahedrons, but the base icosidodecahedron can be reduced to smaller icosahedrons and dodecahedrons back to an original smaller icosidodecahedron.

The following graphic is of a golden section packing arrangement inscribed into an octahedron. This particular graphic is shown from the face view of the octahedron. From this angle you have a hexagonal view. From a side angle you would get a 10 sided view. The interior sphere has a radius of T(squared) while the outer 12 spheres have a radius of T.
