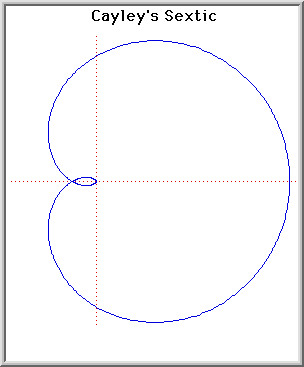
Sestica di Cayley

Equazione cartesiana: 4(x^2+y^2-ax)^3 = 27a^2(x^2+y^2)^2

Equazione polare: r = 4a cos^3(theta/3)

Questa curva fu studiata per primo da Maclaurin ma studiata in dettaglio da Cayley.

Il nome sestica di Cayley e' dovuto a R. C. Archibald che tento' di classificare le curve in un articolo pubblicato a Strasburgo nel 1900.

L'evoluta della sestica di Cayley e' una nefroide curve.

Altri siti web

University of Virginia, USA

JOC/EFR/BS Gennaio 1997
Traduzione di Mike Notte
Siete pregati di notificare Mike Notte di qualsiasi improprieta' di lingua italiana. Grazie.
Per la bibliografia, per esaminare le Curve Associate, e per operare interattivamente sulla curva usando Java, andare al testo originale: www-groups.dcs.st-and.ac.uk/~history/