Equazioni quadratiche, cubiche e di quarto grado

Circa il 300 AC Euclide sviluppo' una soluzione geometrica che, benche' in seguito dei matematici la usassero per risolvere equazioni quadratiche, sirisolveva a trovare una lunghezza che, nella nostra notazione, era la radice di un'equazione quadratica. Euclide non aveva la nozione di equazione, coefficienti ecc., ma lavorava con quantita' puramente geometriche.

Matematici Hindu svilupparono di piu' il metodo babilonese cosicche' Brahmagupta (598-665 DC) ci da' un metodo quasi moderno che accetta quantita' negative. Egli uso' anche delle abbreviazioni per quantita' incognite, di solito la lettera iniziale di un colore. Qualche volta parecchie incognite occorrevano in un singolo problema.

Gli Arabi non sapevano dei progressi fatti dagli Hindus e cosi' essi non avevano quantita' negative ne' abbreviazioni per le incognite. Pero' al'Khwarizmi (c 800) diede una classificazione di differenti tipi di quadratiche (benche' solo esempi numerici di ognuna). I differenti tipi vennero fuori perche al'Khwarizmi non aveva lo zero ne' numeri negativi. Egli dedico' sei capitoli, ognuno per un tipo diverdso di equazione. Le equazioni erano composte di tre tipi di quantita' e cioe': radici, quadrati di radici e numeri come lo x, x e numeri.

1. Quadrati uguali a radici.
   
2. Quadrati uguali a numeri.
   
3. Radici uguali a numeri.
   
4. Quadrati e radici ugualia numeri, come per esempio x + 10x = 39.
   
5. Quadrati e numeri uguali a radici, come per esempio x + 21 = 10x.
   
6. Radici e numeri uguali a quadrati, come per esempio 3x + 4 = x.

Abraham bar Hiyya Ha-Nasi, spesso noto col nome latino Savasorda, e' famoso per il suo Liber embadorum pubblicato nel 1145 che fu il primo libro pubblicato in Europa a dare la soluzione completa dell'equazione quadratica.

Una nuova fase della matematica ebbe inizio in Italia verso il 1500. Nel 1494 la prima edizione della Summa de arithmetica, geometrica, proportioni et proportionalita, nora nota come la Summa, appari'. Era stata scritta da Luca Pacioli benche' e' difficile trovare il nome dell'autore nel libro. Fra Luca appare in piccoli caratteri ma non sul frontespizio. In molti modi il libro e' piu' un sommario della conoscenza di quel tempo, e non da' avanzamenti della conoscenza. Pero' la notazione e la disposizione dei calcoli ha uno stile quasi moderno:

                      6.p.R.10
                     18.m.R.90
                  ____________
  108.m.R.3240.p.R.3240.m.R.90
hoc est 78.

(6+10)(18-90)=(108-3240+3240-900)
che e' 78.

Pacioli non discusse le equazioni cubiche ma discute quelle di quarto grado. Egli dice che, nella nostra notazione, x = a + bx puo' essere risolto con metodi quadratici ma x + ax = b e x + a = bx sono impossibili allo stato presente della scienza.

Scipione dal Ferro (1465-1526) tenne la Cattedra di Aritmetica e Geometria all'Universita' di Bologna e certamente deve avere incontrato Pacioli che insegno' a Bologna nel 1501-2. dal Ferro ha ricevuto credito di aver risolto equazioni cubiche algebricamente, ma il quadro e' un po' piu' complesso. Il problema era di trovare le radici con addizioni, sottrazioni, moltiplicazioni e divisioni e prendendo radici di espressioni nei coefficienti. Noi crediamo che dal Ferro poteva solo risolvere equazioni cubiche della forma x + mx = n. Fifatti cio' e' tutto quello che si richiede. Perche', data la forma cubica y - by + cy - d = 0, metti
y = x + b/3 per ottenere

x + mx = n dove m = c - b/3, n = d - bc/3 + 2b/27.

Pero', senza la conoscenza indiana dei numeri negativi, dal Ferro non sarebbe stato capace di usare la sua soluzione del solo caso per risolvere tutte le equazioni cubiche. Rimarchevolmente, dal Ferro risolvette quella equazione cubica circa il 1515 ma tenne il suo lavoro totalmente segreto fino a poco prima della sua morte, nel 1526, quando la rivelo' al suo studente Antonio Fior.

Fior era un matematico mediocre e molto meno capace di mantenere segreti di dal Ferro. Subito dicerie cominciarono a circolare a Bologna che l'equazione cubica era stata risolta. Nicolo of Brescia, noto come Tartaglia che significa "quello che balbetta", spinto da quelle dicerie, riusci' a risolvere equazioni della forma
x + mx = n e non tenne la sua scoperta segreta.

Fior sfido' Tartaglia a una prova pubblica: le regole erano che ognuno dava all'altro 30 problemi che dovevano essere risolti entro 40 o 50 giorni. Il vincitore sarebbe stato chi ne risolvesse di piu' ma un piccolo premio era offerto per ogni problema. Tartaglia risolvette tutti i problemi di Fior nel tempo di 2 ore, perche' tutti i problemi sottomessi da Fior avevano la forma x + mx = n poiche' egli credeva che Tartaglia sarebbe stato incapace di risolvere quel tipo. Pero' solo 8 giorni prima che i problemi venissero raccolti, Tartaglia aveva trovato il metodo generale per tutte le cubiche.

Notizia della vittoria di Tartaglia arrivo' a Cardano a Milano dove egli si stava preparando a pubblicare Practica Arithmeticae (1539). Cardano invito' Tartaglia a fargli visita e, dopo molta persuasione, ottenne che gli divulgasse il segreto della sua soluzione dell'equazione cubica. Cio' fu fatto da Tartaglia, ma solo dopo essersi fatto promettere da Cardano di tenere il segreto fino a che Tartaglia non l'avesse pubblicata lui stesso. Cardano non mantenne la promessa. Nel 1545 egli pubblico' Ars Magna il primo trattato di algebra in latino.

Questa e', in notazione moderna, la soluzione di Cardano di
x + mx = n. Notate che

(a - b) + 3ab(a - b) = a - b

b = m/3a cosi' a - m/27a = n,
i.e.
a - na - m/27 = 0.

Cardano noto' qualcosa di strano quando egli applico' la sua formula a certe cubiche. Nel risolvere x = 15x + 4 egli ottenne un'espressione che coinvolgeva 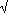-121. Cardano sapeva che non si puo' prendere la radice quadrata di un numero negativo eppure sapeva che x = 4 era una soluzione dell'equazione. Scrisse a Tartaglia il 4 Agosto 1539 in un tentativo di chiarire la difficolta'. Tartaglia certamente non capi'. In Ars Magna Cardano da' un calcolo con "numeri complessi" per risolvere un simile problema, ma in verita' non capiva i propri calcoli che egli disse erano tanto fini da essere inutili.

Dopo che Tartaglia aveva mostrato a Cardano come risolvere le cubiche, Cardano incoraggio' un suo studente, Lodovico Ferrari, ad esaminare le equazioni di quarto grado. Ferrari riusci' a risolverle con un metodo che e' forse il piu' elegante di tutti quelli trovati per risolvere tale problema. Cardano pubblico' tutti e 20 i casi di equazioni di quarto grado in Ars Magna . Ecco, ancora in notazione moderna, la soluzione di Ferrari del caso: x + px + qx + r = 0. Prima completa il quadrato per ottenere

x + 2px + p = px - qx - r + p
i.e.
(x + p) = px - qx - r + p

(x + p + y) = px - qx - r + p + 2y(x + p) + y

= (p + 2y)x - qx + (p - r + 2py + y) (*)

(-q) -4(p + 2y)(p - r + 2py + y) = 0.

(q - 4p + 4 pr) + (-16p + 8r)y - 20 py - 8y = 0

Ora sappiamo come risolvere le cubiche e cosi' risolviamo per y. Con questo valore di y il lato destro di (*) e' un quadrato perfetto e cosi', prendendo la radice quadrata dei due lati, otteniamo una quadratica in x. Risolvi questa quadratica ed avrai la soluzione richiesta per l'equazione quartica.

Il caso irriducibile della cubica, e cioe' il caso dove la formula di Cardan porta alla radice quadrata di numeri negativi, fu studiato in dettaglio da Rafael Bombelli nel 1572 nel suo lavoro Algebra .

Negli anni dopo l'Ars Magna di Cardan molti matematici contribuirono alla soluzione di equazioni cubiche e di quarto grado. Viète, Harriot, Tschirnhaus, Eulero, Bezout e Descartes tutti inventarono dei metodi. I metodi di Tschirnhaus vennero estesi dal matematico svedese E S Bring verso la fine del 18mo secolo.

Thomas Harriot apporto' parecchi contributi. Uno dei piu' elementari per noi, ma che mostra un notevole miglioramento nella comprensione, fu l'osservazione che se x = b, x = c, x = d sono soluzioni di una cubica, allora la cubica e'

(x - b)(x - c)(x - d) = 0.

x + 3bx = 2c

e - 2ce = b

e = c +(b + c).

e(e - 2c) = b cosicche' b/e = -c +(b + c).

Leibniz scrisse una lettera a Huygens nel marzo 1673. In essa egli fece molti contributi alla comprensione delle equazioni cubiche. Forse quella che piu' colpisce e' una verifica diretta della formula di Cardan-Tartaglia. Questo Leibniz fece ricostruendo la cubica dalle sue tre radici (come date dalla formula) secondo come Harriot riteneva in generale. Nessuno prima di Leibniz sembrava avesse pensato a questo metodo diretto di verifica. Quella fu la prima vera dimostrazione algebrica della formula, dacche' tutte le dimostrazioni precedenti erano state di natura geometrica.