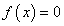
以
x=k
作初始值
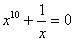
以
x = i
作初始值
| <CMPLX> |
|---|
| Goto 3: Lbl 0: M M ³ ³ + M -1 → A: Goto 2: |
| Lbl 3: ? → M: ? → B: Lbl 4: 0 → C: |
| Lbl 1: Goto 0: Lbl 2: |
| C = 0 => B M– => A → C => Goto 1: |
| A = C => B M+ => Goto 5: |
| B + BC ÷ ( A – C M+: |
| Lbl 5: M ◢ Goto 4 |
| 86 Bytes |
註:
冪運算子 "^" 並不適用於複數
k EXE dx EXE
x1 EXE
x2 EXE
x3 EXE ...
0.354295012 + 1.01790267i EXE
0.212871259 + 0.940495832i EXE
0.129042893 + 1.00798382i EXE
0.133029109 + 0.9853219i EXE
0.144559063 + 0.985614051i EXE
0.143970985 + 0.990866787i EXE
0.141878954 + 0.990489856i EXE
0.142038603 + 0.98963589i EXE
...
(正確答案 = 0.14231481085+0.989821431509i)