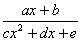
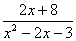
a EXE b EXE
c EXE d EXE e EXE
1 EXE -2 EXE -3 EXE
m EXE n EXE
A EXE B EXE
(即
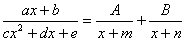 )
)
3.5 EXE -1.5 EXE
(
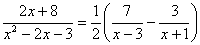 )
)
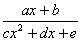
( cx²+dx+e有重根)
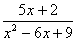
a EXE b EXE
c EXE d EXE e EXE
1 EXE -6 EXE 9 EXE
m EXE m EXE ( 重根)
A EXE B EXE
(即
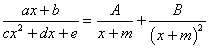 )
)
5 EXE 17 EXE
(
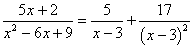 )
)
Casio50 » fx-3x50P » Programs 程式集 » Polynomials 多項式 »
本式可把一分數 —— 其分子為一線性方程而分母為二次方程 —— 化為兩個部份分式.
| <COMP> |
|---|
| ? → A : ? → B : ? → C : ? → D : ? → M : |
| D ² – 4 C M : |
| ( D – √ Ans ) ÷ 2 C → X ◢ D ÷ C – X → Y ◢ |
| Y – X → D => Goto 1 : |
| B C – A X → B : A C → A : Goto 2 : |
| Lbl 1 : ( B – A X ) ÷ C D → M : ( A Y – B ) ÷ C D → B : M → A : |
| Lbl 2 : A ◢ B |
| 109 Bytes |
| 一般操作 | 例子 |
|---|---|
把以下化為部份分式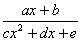 |
把以下化為部份分式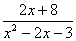 |
| 啟動程式 | 按 Prog 1 |
| 輸入係數 a EXE b EXE c EXE d EXE e EXE |
2 EXE 8 EXE 1 EXE -2 EXE -3 EXE |
| 顯示答案 m EXE n EXE A EXE B EXE (即 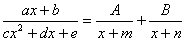 ) )
|
-3 EXE 1 EXE
3.5 EXE -1.5 EXE ( 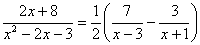 ) )
|
把以下化為部份分式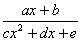 ( cx²+dx+e有重根) |
把以下化為部份分式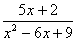 |
| 啟動程式 | 按 Prog 1 |
| 輸入係數 a EXE b EXE c EXE d EXE e EXE |
5 EXE 2 EXE 1 EXE -6 EXE 9 EXE |
| 顯示答案 m EXE m EXE ( 重根) A EXE B EXE (即 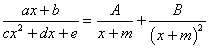 ) )
|
-3 EXE -3
EXE (重根) 5 EXE 17 EXE ( 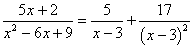 ) )
|
| A | A |
|---|---|
| B | B |
| C | c |
| D | n-m |
| X | m |
| Y | n |
| M | e or A |