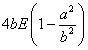
m EXE
E
(即是橢圓周界約為 4 × 3 × 1.3221 = 15.8652)
Casio50 » fx-3x50P » Programs 程式集 » Special Functions 特殊函數 »
本式求 Complete Elliptic Integral of the Second Kind E(m) 的約值.
| <COMP> |
|---|
| ? → A : |
| A = 0 => π ÷ 2 → B => Goto 0 : |
| A = 1 => 1 → B => Goto 0 : |
| ( .5976254639 A ² – 2.022567615 A + 1.570797835 ) ÷ ( .0142816 A ³ + .167474 A ² – 1.03755 A + 1 → B : |
| Lbl 0 |
| 106 Bytes |
| 一般操作 | 例子 |
|---|---|
| 求 E(m) 的值 | 求一個長短半軸分別為 2 和 3 的橢圓的周界. |
若一個橢圓的長短半軸分別為 a 和 b, 則其周界為 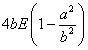 |
|
| 啟動程式 | 按 Prog 1 |
| 輸入資料 m EXE |
1 – 2² ÷ 3² EXE |
| 顯示答案 E |
1.322111804 (即是橢圓周界約為 4 × 3 × 1.3221 = 15.8652) |
| A | m |
|---|---|
| B | E |
| C | |
| D | |
| X | |
| Y | |
| M |
Complete Elliptic Integral of the Second Kind 的定義為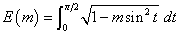 ,
其中 0 ≤ m ≤ 1.
,
其中 0 ≤ m ≤ 1.
本式可在 m = 0 或 1 時給出準確值; 0 < m ≤ 0.8 時約四至五個小數位; 0.8 < m < 1 時約兩至三個小數位, 且誤差會隨著 m 增大.