複角公式

--------------------(1)--------------------

sinA/cosA=(a/c)/(b/c)=a/b=tanA

--------------------(2)--------------------

a²+b²=c²

a²/c²+b²/c²=1

∴sin²A+cos²A=1

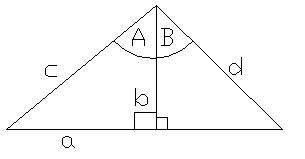
--------------------(3)--------------------

(1/2)[sin(A+B)](cd)=(1/2)[sin(A)](bc)+(1/2)[sin(B)](bd)

sin(A+B)=[sin(A)](b/d)+[sin(B)](b/c)

∴sin(A+B)=sinAcosB+cosAsinB

--------------------(4)--------------------

代B=-B入(3)

sin[A+(-B)]=sinAcos(-B)+cosAsin(-B)

∴sin(A-B)=sinAcosB-cosAsinB

--------------------(5)--------------------

代A=π/2-A入(4)

sin[(π/2-A)-B]=sin(π/2-A)cosB-cos(π/2-A)sinB

cos[π/2-(A+B)]=cosAcosB-sinAsinB

∴cos(A+B)=cosAcosB-sinAsinB

--------------------(6)--------------------

代B=-B入(5)

cos[A+(-B)]=cosAcos(-B)-sinAsin(-B)

∴cos(A-B)=cosAcosB+sinAsinB

--------------------(7)--------------------

根據(1)，tan(A+B)=sin(A+B)/cos(A+B)

=(sinAcosB+cosAsinB)/(cosAcosB-sinAsinB)

=[(sinAcosB)/(cosAcosB)+(cosAsinB)/(cosAcosB)]/[(cosAcosB)/(cosAcosB)-(sinAsinB)/(cosAcosB)]

=[tanA+tanB]/[1-tanAtanB]

∴tan(A+B)=(tanA+tanB)/(1-tanAtanB)

--------------------(8)--------------------

代B=-B入(7)

tan[A+(-B)]=[tanA+tan(-B)]/[1-tanAtan(-B)]

∴tan(A-B)=(tanA-tanB)/(1+tanAtanB)

--------------------(9)--------------------

根據(3)，代入B=A

sin(A+A)=sinAcosA+cosAsinA

∴sin(2A)=2sinAcosA

--------------------(10)--------------------

根據(5)，代入B=A

cos(A+A)=cosAcosA-sinAsinA

∴cos(2A)=cos²A-sin²A

--------------------(11)--------------------

根據(10)，代入sin²=1-cos²A

cos(2A)=cos²A-(1-cos²A)

∴cos(2A)=2cos²A-1

--------------------(12)--------------------

根據(10)，代入cos²=1-sin²A

cos(2A)=(1-sin²A)-sin²A

∴cos(2A)=1-2sin²A

--------------------(13)--------------------

根據(7)，代入B=A

tan(A+A)=(tanA+tanA)/(1-tanAtanA)

∴tan(2A)=(2tanA)/(1-tan²A)

--------------------(14)--------------------

sin(3A)=sin(A+2A)

=sinAcos(2A)+cosAsin(2A)

=sinA[1-2sin²A]+cosA[2sinAcosA]

=sinA-2sin³A+2sinAcos²A

=sinA-2sin³A+2sinA[1-sin²A]

=sinA-2sin³A+2sinA-2sin³A

=3sinA-4sin³A

∴sin(3A)=3sinA-4sin³A

--------------------(15)--------------------

cos(3A)=cos(A+2A)

=cosAcos(2A)-sinAsin(2A)

=cosA[2cos²A-1]-sinA[2sinAcosA]

=2cos³-cosA-2sin²AcosA

=2cos³-cosA-2[1-cos²A]cosA

=2cos³-cosA-2cosA+2cos³A

=4cos³A-3cosA

∴cos(3A)=4cos³A-3cosA