正弦公式、餘弦公式

--------------------(28)--------------------

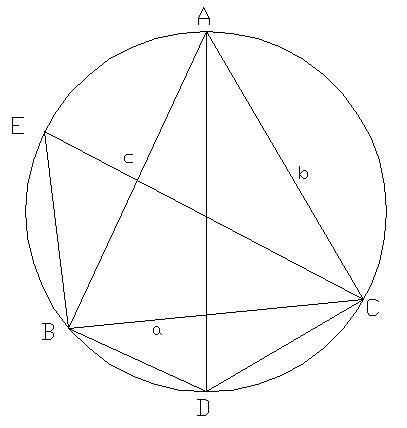
在上圖，∠ABD=∠ADC=∠CBE=90^。，∠BAC=∠BEC，∠ABC=∠ADC，∠ACB=∠ADB，AD=CE=2r

∴sin∠BAC=sin∠BEC=a/(2r)

sin∠ABC=sin∠ADC=b/(2r)

sin∠ACB=sin∠ADB=c/(2r)

∴a/sin∠BAC=b/sin∠ABC=c/sin∠ACB=2r

∴(sin∠A)/a=(sin∠B)/b=(sin∠C)/c

--------------------(29)--------------------

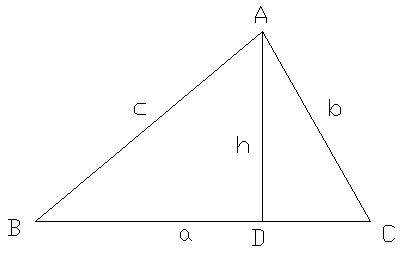
在上圖，∠ADC=∠ADB=90^。

在△ACD，h²=b²-CD²，CD=bcos∠C

在△ABD，h²=c²-(a-CD)²

∴b²-CD²=c²-[a²-2aCD+CD²]

b²=c²-a²+2abcos∠C

∴a²+b²-c²=2abcos∠C