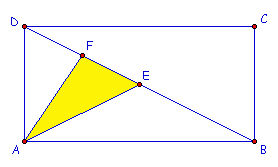
Question 4

In rectangle ABCD, E is the midpoint of BD, F is the midpoint of ED, AD is 10 cm, and AB is 20 cm. What's the area of AEF?

First Solution:

The yellow triangle is 1/8 of the rectangle.

1. The area of the triangle ABD is 1/2 of the area of

the rectangle ABCD because triangle ABD is congruent to the triangle

BCD because of the property SSS.

2. Area of the triangle ADE is 1/2 of the area of the triangle ABD

because area of the triangle ADE is the same as the area of triangle

AEB. The triangles have equal bases ED = EB and the same height (

AE)

3. Area of the triangle AEF is 1/2 of the area of the triangle ADE as

triangles AEF and AFD have equal area because bases FE = FD and they

share the same height (AF).

4. The area of the rectangle is 20 x 10 = 200. So the area of the yellow triangle is 200 / 8 = 25 sq. cm

Second Solution:

Triangle ABD has a base of 20cm and a height of 10cm.  The area of the triangle is 200/2= 100 sq. cm.

Looking at the triangle ABD, create point P on DB so that AP is

perpendicular to DB.  It would be the height of both triangles ADE and ABE.

The bases BE and DE are congruent, because E is a midpoint.

. So Triangle AED=AEB.

Triangle AED+AEB=100 sq. in.

Also, AF is the median of the triangle, therefore triangle AEF=triangle ADF.

The area of AEF= 100/2/2= 25 sq. cm.