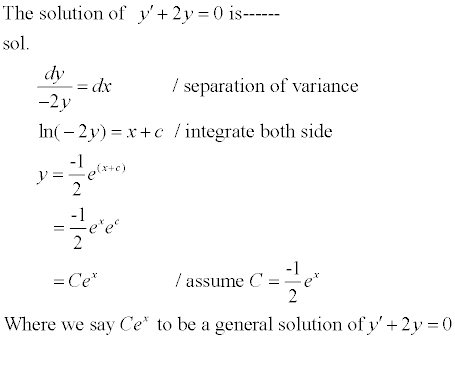The concept of Differentiable Equation

The concept of Differentiable Equation

1. Introduction

Classically, the meaning of derivative is how many of y (dependent variable) be change while x (independent variable) has a little increment. That is, it implies, differentiable equation just can describe a short term phenomena. However in real world, some phenomena just can be formulated by short term information. When we seek to obtain a long term description from a short term description, it means integrating a differentiable equation so as to evaluate the general solution. And it is the meaning of solving a differential equation.

2. Solution of differentiable equation

Normally, we usually distinguish the solution of differentiable equation to be general solution or particular solution.

2.1 General Solution

When a anti-derivative of a differentiable equation be find out without a particular constant of integration (denote its as c, in here) .

for instance

2.2 Particular Solution

Particular solution is derived from general solution which restrict by a set of initial conditions. For example, in the pervious example, if we point out that the initial condition of the general solution is y(1)=2, then

So ,then, one can find that the difference between general and particular solution is is it has a particular constant of integration (normally, denoted as c)