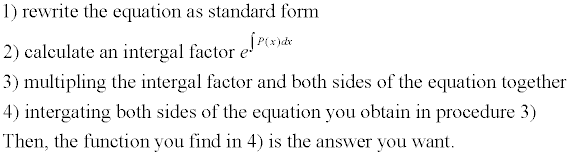Solving The First-Order Linear Differentiable equation

¡@

1. Introduction

      First-order linear differentiable equation usually be used for formulating some financial and physical phenomena, sure as Annuities, Bank Accounting Model and air resistance (as you see later). In this text, we will illustrate how to solve this kind of equation.

¡@

¡@

2. Solving first-order linear differentiable equation

¡@
¡@ 2.1 Standard Form of first-order linear differentiable equation
The standard form of first-order linear differentiable equation is side to be:

Where P(x) and Q(x) is a differentiable function of x.
     

      Note that when Q(x)=0, we said the function to be homogeneous, whereas to be non-homogeneous. If a function is a homogeneous equation, one can solve its by separation variables. However, if it is a alternative form, then the solving approach is illustrated as following procedure:

¡@
Approach of solving first-order linear non-homogeneous equation:

Or be written mathematically

<-----The proof of this formula is somewhat complicated. However if one see mathematics as his/er mind (as I do), then please click the following link:

¡@

PROOF

¡@

Rather than remember this formula, one can see that :

Therefore we can rewrite the procedure 4 of the pervious Approach:
Approach of solving first-order linear non-homogeneous equation:

¡@

¡@

3. Application------Annuities
¡@ ¡@

(sorry, this part is under construction)

¡@

¡@

Reference

In fact following references just are undergraduate level, lacking advanced mathematical treatment.
¡@
About first-order linear differentiable equation with several application, see
1.<<Calculus of a Single Variable>> 8th editon, by Larson, Hostetler, Edwards, pp432-438
¡@
About the proof of the first-order linear differentiable equation-formula, we recommend that
2.<<Calculus volume II>>(in Chinese) QingHun University Pass, edited by SunYi, ZhaoJianHua, WangGuoMing, HanYan,  pp170-171
¡@
About Annuities without serious mathematical treatment, see
3.<<Finance>> by Zvi Bodie, Robert C.Merton, pp118-125

¡@