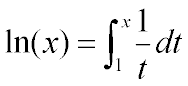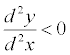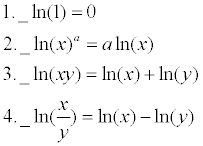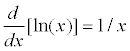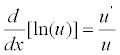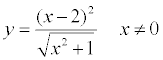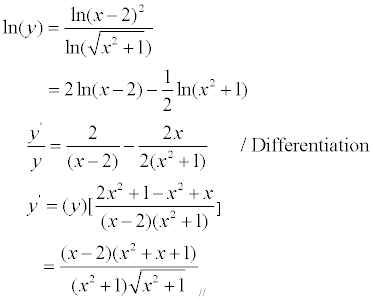The basic level of Natural Logarithmic Function, its Differentiation and Integration

　

1. Introduction
　

 

　

 　

1.1 The definition of natural logarithmic (log, for short, in here) function

The definition of natural log function

where x >0

So by this definition. we obtain those following properties of natural log function:

(1)The domain and the range of the function is    and  respectively
　 (2)The function is continuous, increasing, and one to one
　

(3)  

　

　 　

1.2 The logarithmic law

The log law

where x and y are positive numbers; u  is rational

One will find that how those laws are useful, when we study about differentiation and integration later. 

2. Differentiation of natural log function

　 　

2.1 derivative of natural log function

let u be a function of x, then by the chain rule, obtain

　

So, then, combating those natural log law (1.2) and derivative (2.1) is a useful approach to solve some differentiation problems.

e.g.  

sol.

      At the first glance, one may be solve this problem depend on some basic rule of differentiation------solving the problem by Quotient rule firstly, then using Chain rule to find the answer out. However, by the natural log law, you can rewrite the problem to be:

so that, obtain the answer.

　

3. Log rule for integration

　 　

3.1 Log rule for integration

By the differentiation of natural log, we are able to obtain:

This is, hence, by this log rule for integration, we can derive Six basic integration of trigonometric function. However, the proof and the detail are not within the scope in this text. (Perhaps I will introduce its later)

　

This is the end of this text.