Bandul Terbalik

Bandul terbalik adalah bandul yang pusat massanya berada di atas titik poros. Biasanya titik poros dilekatkan pada sebuah pengangkut yang dapat bergerak bebas secara horisontal sehingga disebut pula kereta dan tiang (cart and pole). Bandul biasa (yaitu bandul yang digantung) bersifat stabil, sedangkan bandul terbalik pada dasarnya bersifat tidak stabil. Agar tetap tegak, bandul terbalik harus secara aktif diseimbangkan, antara lain dengan memberi torsi pada titik poros atau dengan menggeser-geser titik poros secara horisontal dengan menggunakan sistem kendali umpan balik.

Bandul terbalik pada sebuah kereta pengangkut

Catatan

Bandul terbalik merupakan problem klasik yang sering dimunculkan dalam pembahasan teori kendali dinamis. Problem ini dijadikan tolok ukur dalam pengujian algoritma kendali (kontroler PID, jaringan syaraf tiruan, kontrol fuzzy, algoritma genetik, dan lain-lain). Problem dapat divariasi dengan menyertakan banyak link sehingga memungkinkan pengendalian gerak kereta untuk menyeimbangkan bandul pada sebuah jungkit.
Bandul terbalik mempunyai kaitan dengan pengendalian roket atau rudal, di mana pendorong roket diposisikan pada bagian bawah benda yang tinggi. Penerapan juga terdapat pada teknik Segway, yaitu perangkat pemindahan barang yang mampu menyeimbangkan diri. Contoh aplikasinya adalah pada menara (crane) pengangkat kontainer di pelabuhan. Ketika menggerakkan kontainer maju atau mundur, menara menggerakkan boks mengikuti gerak kontainer sedemikian rupa sehingga boks tidak pernah terlontar atau berayun. Boks tetap berada secara tepat di bawah operator meskipun digerakkan atau dihentikan mendadak.

Terdapat satu teknik lagi yang mampu menyeimbangkan bandul terbalik, yaitu dengan menggerakkan poros bawahnya secara cepat ke atas dan ke bawah. Jika gerak ini cukup kuat dan cepat maka bandul dapat menstabilkan diri menuju posisi keseimbangan, fenomena yang secara awam sukar dipahami.

Bandul pada poros statis

Persamaan gerak bandul terbalik sama dengan persamaaan untuk bandul normal tapi dengan tanda minus untuk posisi sudut jika diukur dari sumbu vertikal: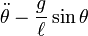

atau:

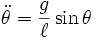
Persamaan di atas ini menyatakan bahwa pendulum terbalik akan bertambah kecepatan jika posisi bandul menjauh dari titik keseimbangan vertikal. Percepatan gerak bandul setara dengan panjang bandul, yang artinya bandul yang panjang akan jatuh lebih lambat dari pada bandul yang pendek. (Oh begitu ya, pantas pemain sirkus memilih galah yang panjang...)

Bandul pada kereta

Persamaan gerak diturunkan menggunakan persamaan Lagrange. Seperti tampak pada gambar, x(t) adalah posisi kereta, q(t) adalah sudut bandul terhadap posisi vertikal dan gaya yang terlibat adalah gravitasi dan gaya luar pada arah sumbu x. Persamaan Lagrange adalah L = T - V dengan L adalah Lagrangian, T adalah energi kinetik dalam sistem dan V adalah energi potensial. L dapat ditulis menjadi: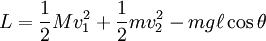

dengan v₁ adalah kecepatan kereta dan v₂ adalah kecepatan gerak massa m. v₁ dan v₂ dapat dinyatakan dalam variabel x dan q dengan menuliskan kecepatan sebagai turunan waktu dari posisi:

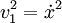
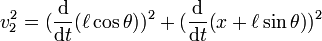
Penyederhanaan persamaan untuk v₂ menghasilkan::

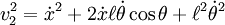
Ekspresi untuk Lagrangian sekarang menjadi:

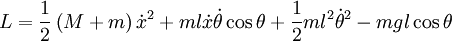
sedangkan persamaan geraknya adalah:

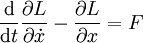
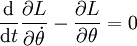
Dengan menukar L pada persamaan-persamaan ini dan melakukan penyederhnaan, akan diperoleh persamaan yang menggambarkan gerak bandul terbalik:

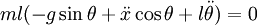
Kedua persamaan ini adalah nonlinier, tetapi karena tujuan sistem kendali adalah untuk menjaga bandul tetap tegak, persamaan ini dapat dilinierkan yang berlaku untuk .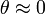

Bandul pada poros osilatif vertikal

Please refer to Wikipedia.

Mengendalikan kereta supaya bandul tetap tegak vertikal

Yang jadi pertanyaan sekarang adalah bagaimana mengendalikan gerak kereta supaya bandul tetap tegak vertikal? Diskusikan dan cobalah buat simulasinya. Gunakan EasyJava Simulation, MatLab, atau software simulasi lainnya (catatan: jangan gunakan software bajakan).