Sistem Linier

Linear Systems

Sistem Linier

Representasi sinyal dalam impuls

Representasi sinyal dalam impuls artinya adalah menyatakan sinyal sebagai fungsi dari impuls, atau menyatakan sinyal sebagai kumpulan dari impuls-impuls. Sembarang sinyal diskret dapat dinyatakan sebagai penjumlahan dari impuls-impuls diskret dan sembarang sinyal kontinyu dapat dinyatakan sebagai integral impuls.

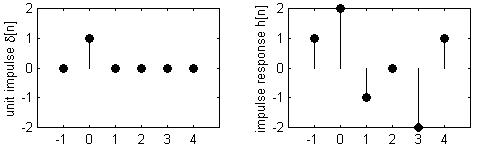
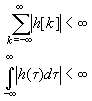Gambar 4.1. Sinyal x[n] (kiri atas) dan sinyal-sinyal penyusunnya Pada gambar kiri atas, terlihat sinyal x[n] terdiri atas lima impuls. Gambar yang lain adalah impuls-impuls penyusun gambar kiri atas. Impuls-impuls penyusun dapat diperoleh dengan mengalikan sinyal x[n] dengan impuls satuan yang digeser. Sinyal impuls x[0]d[n] diperoleh dengan mengalikan x[n] dengan d[n]. Sinyal impuls x[1]d[n-1] diperoleh dengan mengalikan x[n] dengan d[n-1]. Dan akhirnya tampak jelas bahwa:
x[n] = x[0]d[n] + x[1]d[n-1] + x[2]d[n-2] + x[3]d[n-3] x[4]d[n-4]

Secara umum, sebuah sinyal diskret sembarang x[n] dapat dinyatakan sebagai penjumlahan impuls-impuls:

Seperti pada sistem diskret, sebuah sinyal kontinyu sembarang dapat dinyatakan sebagai integral dari impuls-impuls:

Konvolusi

Keluaran sebuah sistem disebut juga respon. Jika sinyal berupa unit impulse masuk ke dalam sistem, maka sistem akan memberi respon yang disebut respon impuls (impulse response). Respon impuls biasa diberi simbol h. Jika sistemnya diskret, respon impulsnya diberi simbol h[n] dan jika sistemnya kontinyu, respon impulsnya diberi simbol h(t). Di bawah ini adalah gambar sinyal impuls satuan d[n] dan contoh respon impuls sebuah sistem diskret h[n].

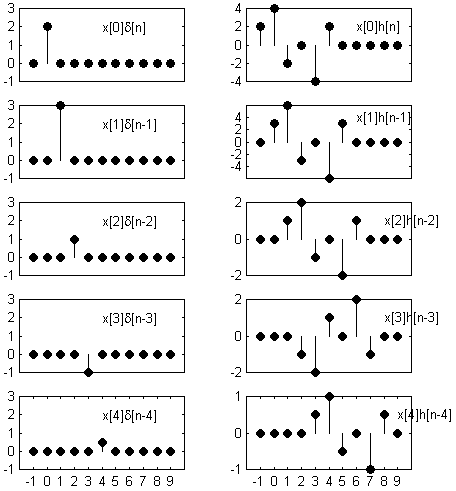
Gambar 4.2. Sinyal impuls satuan (kiri) dan contoh respon impuls (kanan) Jika respon impuls sebuah sistem linier diketahui, maka respon sistem terhadap sembarang bentuk sinyal dapat dihitung. Gambar di bawah ini memperlihatkan bagaimana respon sistem terhadap masukan x[n] dicoba dihitung untuk sistem dengan respon impuls h[n] seperti gambar 4.2 di atas. konvolusi

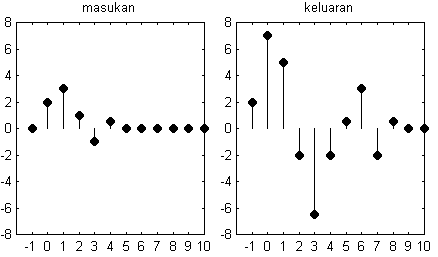
Gambar 4.3. Respon (kanan) terhadap berbagai impuls (kiri). Impuls-impuls merupakan penyusun sinyal x[n]. Respon-respon yang ditunjukkan adalah untuk sistem dengan respon impuls seperti pada gambar 4.2 Pada penghitungan respon sistem terhadap masukan sinyal sembarang x[n], sinyal x[n] diurai menjadi sinyal-sinyal penyusunnya. Setiap sinyal penyusun kemudian dicari responnya. Respon sistem diperoleh dengan menjumlahkan seluruh respon terhadap sinyal penyusun. Dengan kata lain, Sinyal x[n] diurai menjadi sinyal-sinyal x[0]d[n], x[1]d[n-1], x[2]d[n-2] dan seterusnya. Setiap sinyal penyusun akan menghasilkan respon yang mirip dengan respon impuls, tapi berbeda pada letak dan nilai besarnya. Bentuk sinyal x[0]d[n] sama dengan impuls satuan dikali 2, maka responnya sama dengan respon impuls dikali dua atau x[0]h[n]. Bentuk sinyal x[1]d[n-1] sama dengan impuls satuan digeser satu ke kanan dan dikali tiga, maka responnya sama dengan respon impuls digeser satu ke kanan dan dikali tiga atau x[1]h[n-1]. Dan seterusnya. Karena sinyal x[n] dapat disusun dari impuls-impuls penyusun, maka respon sistem terhadap sinyal x[n] dapat disusun dari respon-respon impuls penyusun, yaitu x[0]h[n] + x[1]h[n-1] + x[2]h[n-2] + ... . Setelah dilakukan penjumlahan seperti ini diperoleh gambar respon sistem di bawah ini: hasil

Gambar 4.4. Respon sistem (kanan) terhadap masukan x[n] (kiri). Respon sistem merupakan penjumlahan respon-respon pada gambar 4.3

Jika h[n] adalah respon impuls sistem linier diskret, dan x[n] adalah sinyal masukan maka sinyal keluaran adalah

Rumusan di atas disebut penjumlahan konvolusi.

Jika h(t) adalah respon impuls sistem linier kontinyu, dan x(t) adalah sinyal masukan maka sinyal keluaran adalah

Rumusan di atas disebut integral konvolusi.

Operasi konvolusi mempunyai beberapa sifat operasional:
1. Komutatif : x * h = h * x
2. Asosiatif : (x * g) * h = x * (g * h)
3. Distributif: x * (h1 + h2) = x * h1 + x * h2

Telah disebutkan bahwa jika respon impuls sebuah sistem diketahui, respon sistem terhadap sembarang sinyal dapat dihitung. Sebuah sistem linier dan time-invariant hanya mempunyai satu respon impuls yang tidak pernah berubah. Jadi hubungan antara sebuah sistem dengan respon impuls adalah berkawan satu-satu. Itulah sebabnya respon impuls dapat digunakan menyatakan sebuah sistem dalam pemodelan seperti terlihat pada gambar di bawah ini.

Respon sistem terhadap masukan berupa tangga satuan (unit step) disebut respon step. Hubungan antara unit step dengan unit impulse berkawan satu-satu. Sehingga seperti respon impuls, respon step juga dijadikan gambaran sistem. Penggunaan respon step dalam penggambaran sistem banyak dilakukan pada analisis dan desain sistem kontrol. Sedangkan penggunaan respon impuls lebih banyak dilakukan pada analisis dan desain tapis (filter).

Latihan 4. Sistem Linier.

Buatlah sebuah sinyal diskret sembarang yang paling sedikit mempunyai enam impuls. Beri nama sinyal tersebut x[n]. Setiap mahasiswa tidak diperkenankan membuat bentuk sinyal yang sama. Uraikan sinyal x[n] itu menjadi sinyal-sinyal penyusunnya (seperti contoh pada gambar 4.1 di atas). Gunakan tinta biru atau kertas double folio bergaris biru.

Misalkan terdapat sebuah sistem diskret dengan respon impuls seperti pada gambar. Perhatikan bahwa impuls ketiga mempunyai tinggi sebesar b yaitu digit terakhir NIM saudara (tinggi impuls harap disesuaikan dengan nilai b). Gambarlah respon sistem terhadap masukan sinyal x[n] dari soal 1. Dalam mencari respon sistem, tempuhlah proses seperti pada contoh gambar 4.3 dan gambar 4.4 di atas.

Properti Sistem Linier

Kepemilikan memori. Sistem disebut tanpa memori bila keluaran pada suatu saat hanya tergantung masukan pada saat yang sama. Jadi keluaran tidak tergantung masukan pada saat yang lalu atau masukan pada saat sesudahnya. Karena unit impuls hanya mempunyai nilai di n=0 maka respon impuls sistem linier tanpa memori hanya mempunyai nilai di n=0. Dengan kata lain h[n]¹0 untuk n=0 dan h[n]=0 untuk n¹0. Untuk sistem linier tanpa memori, persamaan sistem adalah y[n]=kx[n] dengan k konstanta, dan respon impulsnya adalah h[n]=kd[n]. Untuk sistem linier kontinyu tanpa memori, persamaan sistem adalah y(t)=kx(t) dengan k konstanta, dan respon impulsnya adalah h(t)=kd(t). Apakah resistor merupakan sistem linier tanpa memori? Jika demikian, manakah konstanta sistemnya?

Invertibilitas. Sistem invertibel adalah sistem yang dapat dicari sistem inversnya. Sistem invers membalik proses sistem utama. Jika keluaran sebuah sistem dimasukkan ke sistem invers, maka keluaran sistem invers itu akan sama dengan masukan dari sistem utama. Ide sistem invers banyak dipakai pada pemodelan sistem dengan menggunakan fungsi polynomial.

Pada gambar terdapat dua sistem dengan respon impuls h dan hI. Jika hI adalah sistem invers dari h, maka akan berlaku bahwa z = y * h, y = x * hI, dan z = x.
Bayangkan h adalah sebuah sistem fisik dan hI adalah rangkaian op-amp. Maka keluaran z dari sistem fisik dapat diperoleh dengan memberi masukan x sebesar nilai z yang diinginkan. Konsep seperti ini diterapkan pada teknik kontrol dengan model invers.

Kausalitas. Sistem kausal adalah sistem yang memberi respon setelah ada masukan. Pengaruh suatu masukan terasa pada saat itu juga dan atau terasa kemudian. Sebuah nilai keluaran dipengaruhi hanya oleh masukan pada saat yang sama atau pada saat yang lalu sehingga

Sinyal impuls satuan mengandung nilai di n = 0 atau t = 0, sehingga respon impuls sistem kausal hanya mengandung nilai di n ³ 0 (diskret) atau di t ³ 0 (kontinyu).

Stabilitas. Sebuah sistem yang stabil akan memberikan respon yang berhingga jika masukannya berhingga. Jika masukan berhingga, maka agar keluaran berhingga haruslah respon impulsnya berhingga. Artinya

=Jangan berhenti berbuat=