LA DELTA DE DIRAC
1.0. Definición intuitiva.
La definición que a continuación expongo de la Delta
de Dirac es la que normalmente se expone en una carrera de ingeniería.
Es una definición que parte de una "abstracción física": un choque
o golpe en mecánica o un "chispazo" en electricidad.
Supongamos que tenemos que empujar un objeto: para ello podemos aplicarle una fuerza
durante un periodo de tiempo t. Si queremos comunicarle una determinada energía
cinética la fuerza f aplicada nos determina la duración t para alcanzar
dicha energía cinética. Si aumentamos f el tiempo necesario será menor.
En el límite cuando t tiende a 0 tendremos que aplicarle una fuerza infinita. Sería
el equivalente físico a un "martillazo": un golpe instantáneo de gran fuerza.
De esta forma definimos la Delta de Dirac como una "función" que vale 0 en todos los
puntos salvo en el origen que vale infinito y cuya area (integral de -infinito a +infinito)
vale 1:

Gráficamente la Delta de Dirac se dibuja como una flecha vertical en el lugar en
que toma el valor infinito.
Los matemáticos más "teóricos" en el tema consideran un sacrilegio
matemático el referirse a la Delta de Dirac como una función. Nótese
que una función es una aplicación de un conjunto en otro y para definir una
función basta con dar la imagen que tiene cada elemento del dominio (conjunto sobre
el que está bien definida nuestra función). Sin embargo para la Delta de Dirac
no es suficiente con dar el valor de sus imágenes: es necesario indicar que su area
vale 1. De hecho la función Delta y la función 2*Delta toman los mismos valores
y sin embargo las consideraremos funciones distintas. Así mismo en determinados contextos
se suele decir que dos funciones son iguales para casi todo t si sólo difieren en
un conjunto finito o numerable de elementos del dominio. En nuestro caso no aplicaremos esta
relación de equivalencia nunca, ya que entonces la función Delta y la función
identicamente nula ( f(t)=0 ) serían equivalentes y no tendríamos entonces nada de
que hablar.
Igual como se define la Delta tendremos que 2*Delta vale 0 en todos los puntos, infinito en el origen
y tiene area 2, -Delta vale 0 en todos los puntos menos en el origen en que vale - infinito y tiene area -1
y Delta(t-a) toma el valor infinito en t=a. Notemos además que la Delta es una "función" par.
2.0. Propiedades inmediatas.
En este apartado se expondrán las propiedades que hacen del conocimiento de la Delta de Dirac algo necesario en el estudio del procesado de señal. Muchas de estas propiedades aparecen en algunos textos como la definición de la delta ( "La Delta es la función que cumple una determinada propiedad, como por ejemplo ser elemento neutro del producto de convolución" ). De hecho en el apartado 4 de este documento se definirá la Delta de Dirac de una forma más rigurosa basándose en una de estas propiedades:
Propiedad 1: Propiedad de muestreo integral.
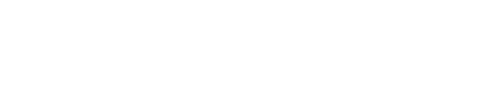
Propiedad 2: Elemento neutro de la Convolución.
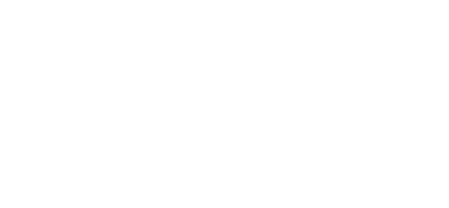
(La convolución puede tener intervalos distintos según el uso que se haga de ésta: en el documento "La transformada de Laplace" se habla de la convolución entre 0 y t ya que todas las funciones allí utilizadas se suponen nulas para t < 0.)
Propiedad 3: La Delta es la Derivada de un escalón.

Propiedad 4: La Transformada de Laplace y de Fourier de la Delta es la función unidad f(t)=1.






