Euclidean Geometry -
Postulates

Euclid - (Third Century B.C.)
Postulates
- The Distance Postulate
- The Ruler Postulate
- The Ruler Placement Postulate
- The Line Postulate
- The Place-Space Postulate
- The Flat Plane Postulate
- The Plane Postulate
- Intersection of Planes Postulate
- The Plane Separation Postulate
- The Space Separation Postulate
- The Angle Measurement Postulate
- The Angle Construction Postulate
- The Angle Addition Postulate
- The Supplement Postulate
- The SAS Postulate
- The ASA Postulate*
- The SSS Postulate*
- The Parallel Postulate**
- The Area Postulate
- The Congruence Postulate
- The Area Addition Postulate
- The Unit Postulate
*The ASA and SSS Postulates can be proved indirectly, so they are theorems as well as postulates. See the Theorem section for more information.
**This Postulate is what defines Euclidean geometry. Otherwise, it could be elliptic geometry (0 parallels) or hyperbolic geometry (infinitly many parallels).
Postulate 1. The Distance Postulate - To every pair of different points there corresponds a unique positive number.
Postulate 2. The Ruler Postulate - The points on a line can be placed in correspondence with the real numbers in such a way that
1. To every point on the line there corresponds exactly one real number;
2. To every real number there corresponds exactly one point of the line; and
3. The distance between any two points is the absolute value of the difference of the corresponding numbers.
Postulate 3. The Ruler Placement Postulate - Given two points P and Q of a line, the coordinate system can be chosen in such a way that the coordinate P is zero and the coordinate of Q is positive.
Postulate 4. The Line Postulate - For every two points there is exactly one line that contains both points.
Postulate 5. The Plane-Space Postulate -
1. Every plane contains at least three non-collinear points.
2. Space contains at least four noncoplanar points.
Postulate 6. The Flat Plane Postulate - If two points of a line lie in a plane, then the line lies in the same plane.
Postulate 7. The Plane Postulate - Any three points lie in at least on plane, and any three noncollinear points lie in exactly one plane.
Postulate 8. Intersection of Planes Postulate - If two different planes intersect, then their intersection is a line.
Postulate 9. The Plane Separation Postulate - Given a line and a plane containing it. The points of the plane that do not lie on the line form two sets such that
1. Each of the sets is convex, and
2. If P is in one of the sets and Q is in the other, then the segment  intersects the line.
intersects the line.
Postulate 10. The Space Separation Postulate - The points of space that do not lie in a given plane form two sets, such that
1. Each of the sets is convex, and
2. If P is in one of the sets and Q is in the other, then the segment  intersects the plane
intersects the plane
Postulate 11. The Angle Measurment Postulate - To every angle there is a real number between 0 and 180.
Postulate 12. The Angle Construction Postulate - Let 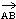 be a ray on the edge of the half-plane H. For every number r between 0 and 180 there is exactly on ray
be a ray on the edge of the half-plane H. For every number r between 0 and 180 there is exactly on ray  , with P in H, such that m< PAB = r
, with P in H, such that m< PAB = r
Postulate 13. The Angle Addition Postulate - If D is in the interior of < BAC,
then m < BAC = m < BAD + m < DAC.
Postulate 14. The Supplement Postulate - If two angles form a linear pair, then they are supplementary.
Postulate 15. SAS Postulate - Every SAS correspondence is a congruence.
Postulate 16. ASA Postulate - Every ASA correspondence is a congruence.
Postulate 17. SSS Postulate - Every SSS correspondence is a congruence.
Postulate 18. The Parallel Postulate - Through a given external point, there is at most one line parallel to a given line.
Postulate 19. The Area Postulate - To every polygonal region there corresponds a unique positive real number.
Postulate 20. The Congruence Postulate - If two triangles are congruent, then the triangular regions determined by them have the same area.
Postulate 21. The Area Addition Postulate - If two polygonal regions intersect only in edges and vertices (or do not intersect at all), then the area of their union is the sum of their vertices.
Postulate 22. The Unit Postulate - The area of a square region is the square of the length of its edges.

