Zenon's Paradoxon

Греческий философ Зенон жил в 490-430 г.г. до нашей эры и был известен своими пародоксами. Бег на перегонки Ахиллеса и черепахи, наверное, самый известный его парадокс.

Греческий герой Ахиллес пытается догнать черепаху, которая находится на некотором расстоянии от него. Но как только он пробегает это расстояние, черепаха успевает проползти вперед. Он пробегает и эту дистанцию, а в это время упорная черепаха снова немного проползает и т.д.
Зенон заключает: Ахиллес никогда не догонит черепаху.

Сегодня математики легко решают этот парадокс практически при помощи школьной математики.

0. D₀ = D ;
1. t₁ = D₀/Va ;
2. D₁ = V_ч * t₁ = D₀(V_ч / V_a) ;
3. t₂ = D₁ / V_a;    D₂ = V_ч * t₂ = D₀(V_ч / V_a)² ;
   ...............

Получается ряд:
D₀[1 + (V_ч/V_a)¹ + (V_ч/V_a)² + ... + (V_ч/V_a)ⁿ + ...] = D₀/(1-V_ч/V_a),     0 < V_ч/V_a < 1 ,
где V_ч - скорость черепахи, V_a - скорость Ахиллеса, D₀ - расстояние между ними в начальный момент времени.
Для V_ч/V_a = 1/2 имеем пункт обгона x = 2D₀.

Но так ли просто решается парадокс Зенона? Вероятно, сам философ подразумевал другое.
Составим алгоритм решения:

...............................
for(i = 1; i < ...; i++){
t_(i) = D_(i-1) / V_a;
D_(i) = V_ч * t_(i);
x_(i) = x_(i-1) + D_(i);
}
............................... [Applet]

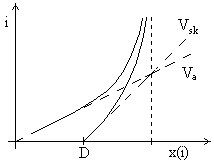
Теперь построим график, где по оси X отложим x_(i) ,а по оси Y - i.
С точки зрения компьютера ось Y будет иметь смысл оси времени t * i . Т.о. для компьютера бег будет происходить все медленнее и медленнее. Так как скорость бегунов постоянная, то речь может идти о кажущемся замедлении времени (примерно как в теории Относительности при движении, приближающегося к скорости света - и это 2500 лет назад!).

Проблема Зенона была в том, что пытаясь представить мысленный эксперимент, он неправильно оперировал с временем:
несмотря на то, что с каждым следующим пробегом отрезки времени уменьшаются, он их рассматривал как постоянные, как следствие, он не имел просто времени, чтобы эту задачу решить в уме до конца.

С другой стороны, ошибка Зенона указывает на физическую невозможность сходимости сходящихся рядов, если одним из их параметров является время. Следовательно, не представляется возможным с помощью компьютера до конца просчитать бесконечные ряды.

Что же делают математики? - Они мысленно перепрыгивают сперва через миллион операций, потом через миллиард, и в конце концов через бесконечность, что скорее всего должно быть связано с идеализмом, чем с такой строгой наукой, как математика. ;-).

---

September 2002, Walter Orlov