Explicación de las Transiciones de Fase del TB.

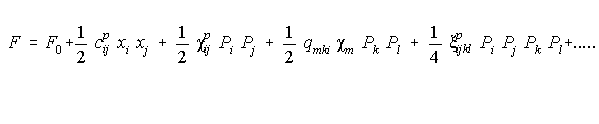
    El estudio en el que se basa lo que a continuación vamos a ver se basa en un trabajo realizado por Devonshire.

    En primer lugar si consideramos la energía libre de Helmholtz y pensamos en la fase cubica del TB. En principio ninguna dirección es preferente con respecto a las demás. Luego los ejes x,y,z, podrán ser considerados por igual.

    Si escribimos la expresión de la energía libre de H y utilizando el convenio de Einstein para sumatorios:

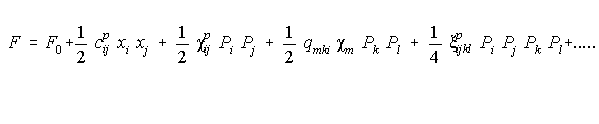
    Donde:

        c_pij Son las constantes elásticas del material.

          c_ij^x Las componentes inversas del tensor de susceptibilidad.

        P_i La componente i de P.

        q_mki Las componentes del tensor de electrostricción ponderado.

        x_i Las deformaciones.

   Donde los tensores se han reducido según unas reglas, de forma que: Si tenemos un tensor con componentes R_ijkl, gracias a las simetrías, podremos convertir este tensor de cuarto orden en otro de segundo, de forma que convertiremos los subíndices (ij Þn) y (kl Þ m), por lo que asignaremos a cada pareja de índices unos nuevos de la forma:

(1•1) Þ 1 ; (2•2) Þ 2 ; (3•3) Þ 3 ; ( 2•3 ) Þ 4; ( 3 • 1) Þ 5; (1 • 2) Þ 6

   Así, las matrices quedarán de la forma: x_ijkl^x =x _nm^x y q_mki = q_nm por lo que obtendremos que:

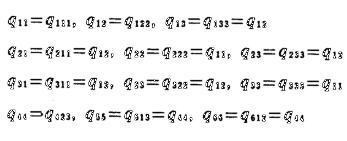
   Por otra parte las matrices para c_pij y para _ij^x sabemos que son de la forma:

   Por lo que para la expresión de F podremos escribir que:

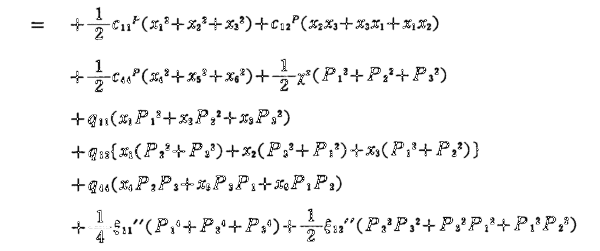
    Donde hemos tomado:

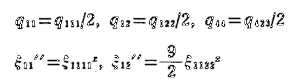
   A partir de esta expresión de F, sabemos que en ausencia de fuerzas externas, podemos escribir la relación:

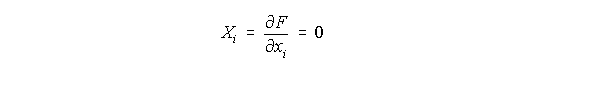
   De donde se obtiene que:

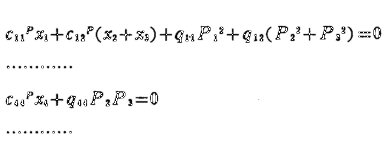
   Despejando las x_i se obtiene que:

   Donde:

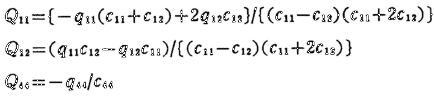
   De estas expresiones se ve que si la polarización espontanea se conoce, entonces podremos conocer la deformación a trabes de las Q_ij. Y si la polarización espontanea, la deformación espontanea y la constante dieléctrica se conoce, entonces podremos determinar los coeficientes q₁₁, q₁₂ y q₄₄.

    Por otra parte, la energía libre de Gibbs, se puede escribir como:

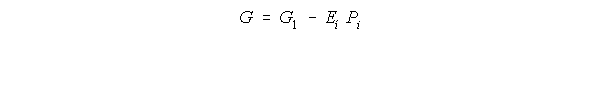
    Donde G₁ es la función elástica de Gibbs. E_i y P_i el campo y la polarización cuando este solo existe en una dirección determinada.

    Si intentamos calcular la función elástica de Gibbs en ausencia de campo externo. Para lo cual, si sustituimos los resultados que hemos obtenido anteriormente para las deformaciones. Los x_i y los valores de las Q_ij en nuestra ecuación de la energía de Helmholtz A1A , obtendremos G₁ hasta el orden cuarto en P. Pero para obtener los resultados que buscamos, necesitamos tener hasta el orden sexto en P. El procedimiento para obtener esto es el mismo seguido para obtener los ordenes inferiores.

   Para el orden sexto en P se obtienen los términos:

   Pero la mayoría de estos términos son despreciables, por lo que se puede hacer una aproximación que nos facilitará las cosas, quedándonos únicamente con el termino:

   Con lo que se llega a la expresión de G₁:

    Donde:

   Donde el hecho de que c=c ^x es una propiedad general de los cristales centrosimétricos por encima del punto de Curie.

   De la expresión de G_l se puede ver que para los términos de orden dos en P son simétricos. Es decir que el sistema cúbico es dieléctricamente isótropo, con tal de que la polarización sea pequeña, mientras que la anisotropía comenzara para valores de la polarización más altos o cuando sea. Por ejemplo, cuando haya alguna dirección anisótropa específica.

   Si consideramos una dirección de polarización específica y aplicamos:

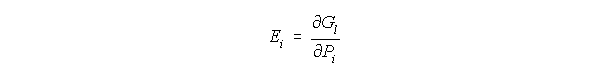
   Obtenemos que:

   De igual forma se hace para las demás componentes del campo eléctrico. Ahora, si consideramos que el campo externo es nulo, eso implica que E₁=E₂=E₃=0. Entonces operando despejamos y obtenemos las siguientes ecuaciones:

   Como podemos ver, tenemos dos posibles soluciones por cada componente nula del campo eléctrico, y como hay tres direcciones, en total podemos tener ocho posibles soluciones. Pero debido a la simetría, sólo podemos tener cuatro soluciones diferentes, que son:

   Como se puede observar, cada una de las soluciones diferentes que hemos encontrado, se van a corresponder con las cuatro circunstancias diferentes que tenemos en TB.

    Pues bien, si recordamos, en ausencia de campo eléctrico, G_l es igual a la energía libre de Gibbs, y como estas situaciones se deben corresponder con mínimos de la Energía libre de Gibbs. Derivando e igualando a "0" dicha expresión, podríamos encontrar las cuatro situaciones diferentes, por lo que se puede deducir que la Energía libre de Gibbs, podrá expresarse por partes de la forma:

   Donde cada uno de las expresiones se corresponden con cada uno de los términos de las expresiones anteriores, de las cuales se pueden derivar directamente.

Por otra parte de los cuatro coeficientes que se observan, tres de ellos se pueden medir cerca del punto de Curie. Para ello sabemos que:

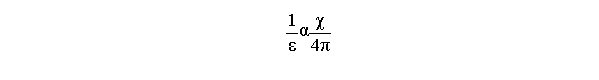
   Luego:

    De aquí, se obtiene valores de C, según el autor, de:

C = 1,25 10⁵ ºC

C = 1,7 10⁵ ºC

   Esto es curioso por que se obtiene que T_c-T₀ = 10 u 11 ºC. Es decir, que la temperatura de Curie, no coincide con T₀, como se puede observar en la siguiente gráfica:

   Por otra parte, si recordamos que:

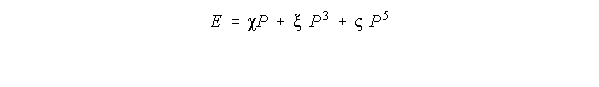
    Y si tenemos que E = 0, entonces, se podrá deducir que:

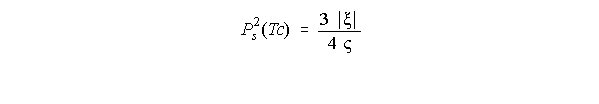
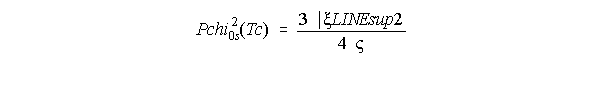
    Con lo que podemos determinar c_0, y x₁₁ de forma que:

   Donde según los autores, tenemos los valores:

V = 3,7 10-21 cgs

x₁₁ = -4.4 10 -12 ;  x₁₁ = -1,17 10 -12

   Ahora, Ga, Gb, Gc y Gd, muestran los valores de G mínimos para T<Tc, de forma que, para cada función G, obtenemos una representación de los mínimos:

   Ahora los valores de V y x₁₁ no dependen de la temperatura en una primera aproximación y x₁₂ = 5.3 10 ^-12.

   Como se puede observar en la gráfica, en cada uno de los tramos, la funciones de Gibbs que es mínima, cambia, pudiéndose deducir de ellas P en dicho tramo, lo que explica las transiciones y la existencia de la polarización espontanea.

   Los resultados de Devonshire están de acuerdo con los resultados experimentales en las tres transiciones de fase. Ahora, considerando cada termino de forma especifica de la expresión de G₁ en cada fase del TB. Vemos que por ejemplo:

   Por encima de la temperatura de Curie, a los 150 ºC, x₁₁ es negativo, por lo que favorece la polarización espontanea de cristal. En cambio otros coeficientes como c , toman valores positivos muy grandes por lo que la contribución total a G₁ es tal que impide la polarización espontanea.

Cuando la T decrece, entonces c toma calores pequeños como se ha visto según la ecuación:

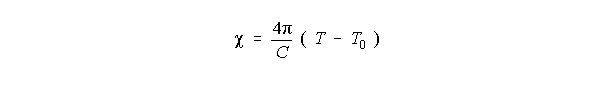
     Donde C = 1,25 10⁵ ºC o C = 1,7 10⁵ ºC y T_c-T₀ = 10 u 11 ºC. Con lo que la oposición a la polarización espontanea se hace despreciable. En este caso si los términos que contienen a ₁₁ en la expresión de G son despreciables, no hay interacciones entre las componentes de la polarización. Luego si la polarización a lo largo de otro eje también reduce G₁ entonces la polarización espontanea podrá darse en la dirección <111>. Sin embargo teniendo términos del tipo:

   Debido a las interacciones entre las componentes de la polarización, la polarización espontanea sólo puede tomar una dirección como la <100>.

   Si la temperatura decrece se hace negativo por debajo de T₀ y ayuda a x₁₁ de forma que hace la polarización espontanea mayor, dando lugar a más componentes. En este caso es V > 0 es quien suprime el incremento de la polarización espontanea y x₁₂ > 0 quien suprime el incremento de las componentes de la polarización.

   Pero como la temperatura disminuye, c decrece. El efecto de c y x₁₁ gana al efecto de x₁₂ cerca de los 0ºC y el numero de componentes de la polarización aumenta a dos. Por otra parte entorno a los -80 ºC por el efecto de c y c₁₁ las componentes de la polarización pueden ser todas.

   Ahora, el hecho de que x₁₁ < 0 y x₁₂ > 0, fue significativamente importante para la transición de fase del T.B. Como puede verse de la Ec.:

A2A

   Los valores x₁₁ y x₁₂ son gobernados por los coeficientes x''₁₁ y x''₁₂ de los términos de orden alto en el aumento de la energía libre del cristal y términos adicionales, originando deformaciones en la red. Como se ha dicho anteriormente en la teoría molecular, las propiedades de la red cristalina del TB sólido, es importante, a diferencia de que sucedería en un líquido o un gas.

   Devonshire, calculó la contribución a la deformación de la red y por sustracción de los términos x₁₁ y x₁₂ obtuvo x''₁₁ y x''₁₂. Al principio, de acuerdo con las ecuaciones:

   La deformación cristalina acompañada por la polarización espontanea en las 3 fases es como sigue:

    Esto se corresponde con la deformación mostrada en la gráfica de parámetros reticulares frente a la temperatura. Y podemos obtener el valor de Q_ij de las ecuaciones anteriores de los resultados experimentales. Sustituyendo, los resultados en las ecuaciones:

   Y usando los valores medios de las q₁₁, q₁₂ y q₄₄ podemos obtener las. Por lo tanto de las ecuaciones A2A podemos obtener x''₁₁ y x''₁₂. Estos toman los siguientes valores:

x''₁₁ = 67,6 10^-12 cgs

x''₁₂ = -0,2 10^-12 cgs

   Por lo que x''₁₁ y x''₁₂ toman signos opuestos a los de x₁₁ y x₁₂ respectivamente. Ahora si pudiéramos observar la transición de fase con x''₁₁> 0 ; quiere decir que la transición de fase seria de 2º orden como se ha debido comentar en un tema anterior y que x''₁₂ < 0 quiere decir que las componentes de polarización, para el mínimo de la energía, daría una polarización espontanea paralela a la dirección <111>.

    son las contribuciones a la electrostricción de la Energía libre de Gibbs. Por lo tanto ''₁₁ - ''₁₂ < 0 significa que los fenómenos que acompañan a la electrostricción por las componentes de la polarización hacen G menor. La electrostricción dada por las ecuaciones b, c y d como se ve en los siguientes valores:

   Q₁₁>0 y Q₁₂<0. Esto es, la red cristalina se expande en la dirección de la polarización y se contrae en las direcciones transversales. Por lo tanto, la electrostricción acompañada por p₁ y otra con p₂ es igual en signo a x₃ pero es opuesto en signo a x₂ y x₃. De esta forma la energía de interacción es positiva.

   En una transición de fase de primer orden, se espera que la relación estre Tcritic y T₀ venga dada por la expresión:

    Lo que está relacionado con que pueda observarse un doble ciclo de histéresis.

   Merz obtuvo la figura de los ciclos de histéresis que vimos anteriormente. Ahora según se muestra en la siguiente gráfica:

    Un ciclo de histéresis proporciona información acerca del campo eléctrico inducido en la transición. Este campo eléctrico se muestra en la gráfica anterior y corresponde al diagrama:

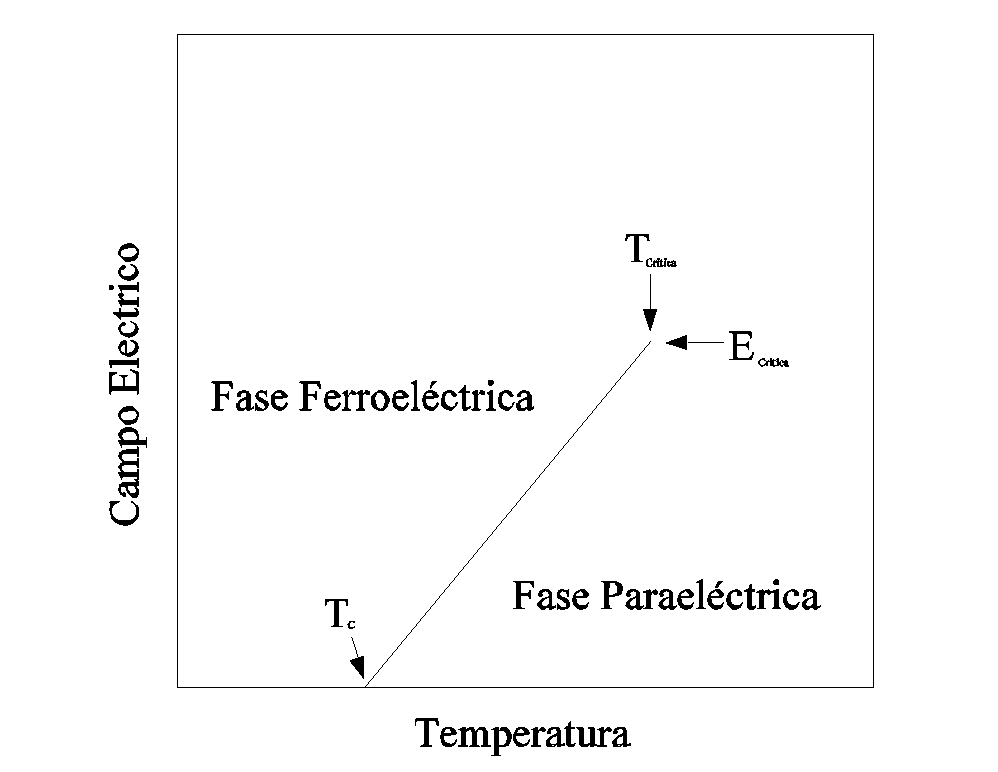
    Como se ha dicho, todas las propiedades del TB están influenciadas por las impurezas. Luego no podemos esperar obtener siempre los mismos resultados.

   En este punto convendría ver de una forma más gráfica algunos de los resultados de esta teoría en relación a los datos experimentales, así, podemos observar las siguientes gráficas en las que se ve que dichos datos se ajustan bastante bien con los experimentos como se puede observar:

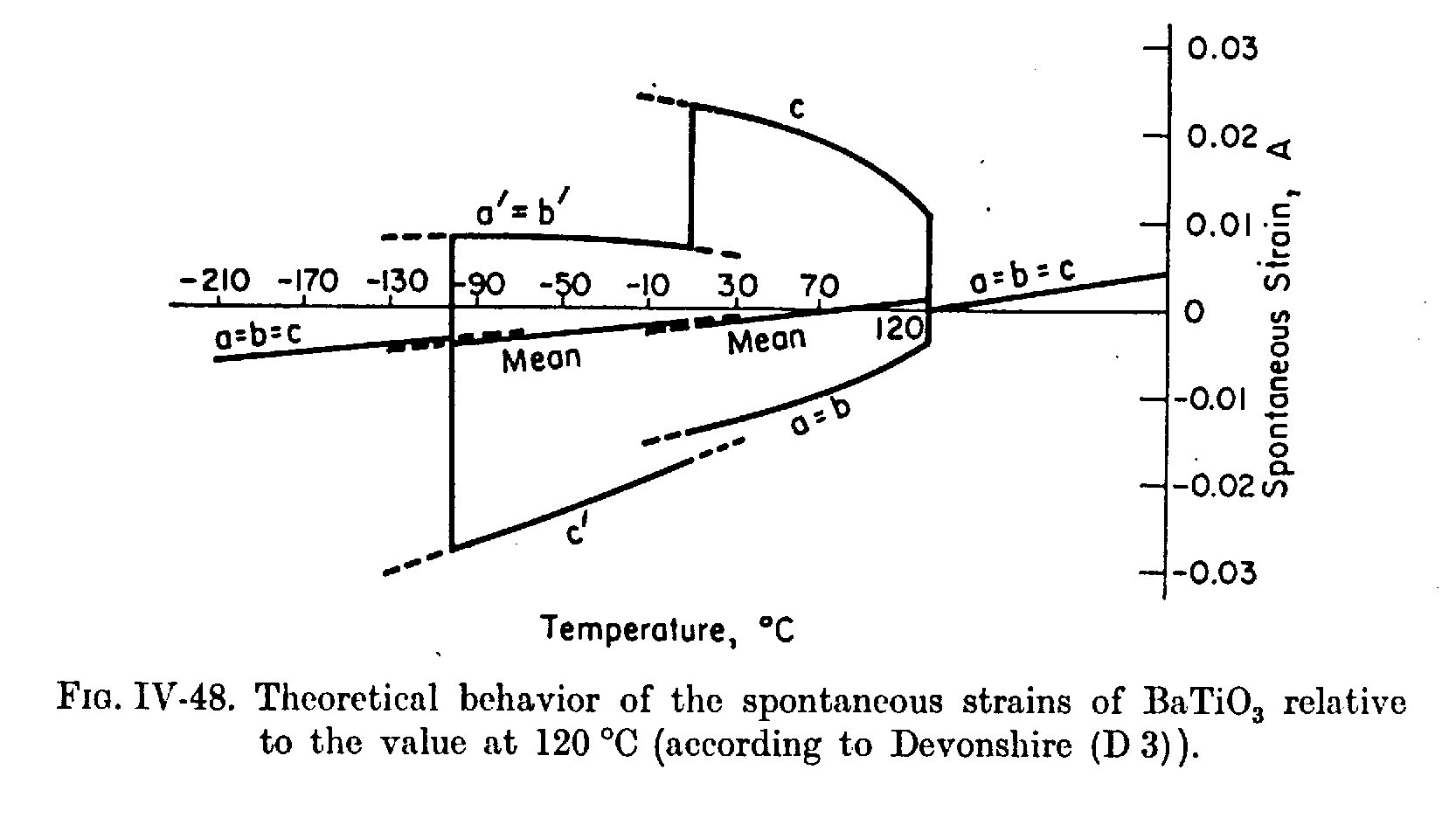
   Vasta con echar un vistazo a las gráficas anteriores en relación a estas.

   Explicaciones relacionadas con la estructura:

   De momento, con lo visto anteriormente, hemos visto una explicación desde el punto de vista energético y usando los resultados experimentales, en definitiva, una teoría fenomenológica para explicar las polarizaciones espontaneas del TB, pero no se ve de una forma clara y concisa por que le TB presenta ferroeléctricidad y cualqueir otro compuesto como puede ser la misma Perovskita (CaTiO₃) no presenta ferroeléctricdad.

    Una de las ideas que se han seguido es:

    Podemos situar el TB dentro de los grupos de compuestos del tipo: A⁺B⁵⁺O₃, A²⁺B⁴⁺O₃ y A³⁺B³⁺O₃, y mezclas entre ellos, donde A⁺ es un ion metálico monovalente Etc. como ya se ha visto.

    Estos óxidos pocas veces presentan una estructura cubica ideal y las transiciones de fases son comúnmente observadas.

    Si ordenamos los A²⁺B⁴⁺O₃ tridimensionalmente deacuerdo con el radio de los iones A²⁺ y B⁴⁺ y colocamos en el otro eje la polarizabilidad del ión A²⁺. Se puede ver que los cristales que tienen un grupo estructural similar se encuentran en la misma región.

    El ordenamiento de los cristales de acuerdo con el radio iónico parece que está más claramente definido si los iones A y B tiene delimitada las estructuras.

    Si seleccionamos los cristales de las estructuras ionicas dadas por A⁺B⁵⁺O₃, A²⁺B⁴⁺O₃. Ordenando estos cristales de acuerdo con el radio iónico de A y B, podemos obtener la siguiente gráfica:

   Donde:

            - Los círculos representan los cristales con un volumen de la celda unidad aproximadamente el mismo que el de la Perovskita.

          - Los puntos negros, los que tienen un volumen que representan un numero entero de veces el volumen de la celda unida de la Perovskita de forma aproximada.

          - Los puntos con una cruz son los que presentan ferroeléctricidad.

    Por ejemplo, si recordamos la estructura de la Perovskita ideal, teníamos esta figura:

   Bien, pues para la temperatura ambiente, el TB presenta esta estructura:

Mientras que la Perovskita, presenta esta otra:

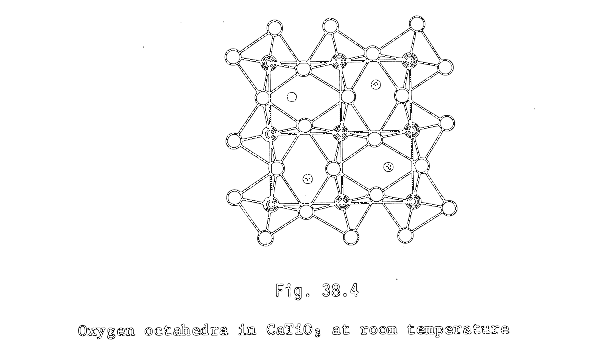
    El hecho que los bordes de los octahedros de oxígeno a lo largo de una dirección reticular valla describiendo un "zig-zag", en vez de ser rectos como en el TB, hace que el parámetro reticular sea del orden del doble que en el TB.

   Luego en la gráfica anterior, pondríamos un punto para la Perovskita y un circulo al TB.

    A la estructura de los exígenos observada en la Perovskita se le suele llamar: Estructura fruncida o arrugada (puckered structure).

   Un criterio para determinar donde deben encontrarse las estructuras de las Perovskitas es el factor de tolerancia definido como:

   Donde R_A, R_B y R_O son los radios reticulares de los iones A, B y del Oxígeno, respectivamente.

Esto se puede deducir por consideraciones geométricas simples a partir de la figura de la Pervskita que teníamos más arriba,(ver apendice I), donde:

                t = 1 Cuando cada ion entra en contacto con sus vecinos

            t > 1 Sobra espacio para el ion B

            t < 1 Sobra espacio para el ion A

   En la representación de los radios iónicos que teníamos, se a dibujado la línea para t = 0,855. Esto sugiere que la estructura fruncida hace reducir el espacio para los iones A. Como se puede ver por la gráfica, por la distribución de los ferroeléctricos, el factor de tolerancia no es un factor esencial para determinar si un material va a ser ferroeléctrico o no. Por otra parte, un radio iónico de B del orden de 0,6 ó 0,7 , vemos que es más favorable para que se de la ferroeléctricidad que cualquier otro.

   La aplicación de un campo eléctrico, puede inducir fases ferroléctricas en la estructura fruncida del PbZrO₃ y NaNbO₃ en un determinado rango de temperaturas. Por lo tanto, la energía libre de la estructura fruncida puede estar muy próxima a la de la fase ferroeléctrica.

    Estos cristales son antiferroeléctricos.

    Takagi y Kinase indicaron que la fase ferroeléctrica del TB tiene una interacción electrostática muy cercana a que de las estructura en la cual el desplazamiento de los iones en las celdas vecinas es antiparalela. Sin embargo, las estructuras de PbZrO₃ y NaNbO₃ son más complicadas que lo que la teoría asume y no está claro si las fases antiferroeléctricas de estos materiales, son reducidas de la estructura fruncida del espaciado excesivo disponible para los inones A o causadas por la interacción electrostática discutida por otros autores.

   Proyecciones de los desplazamientos iónicos a las fases antiferro del PbZrO₃ es antiparalela en el plano ab pero son paralelas en la dirección de c, resultando una polarización espontanea en el eje C. Este hecho muestra una interesante conexión con el hecho de que según el radio de los iónes, vamos a tener una disposición perfectamente paralela o no a la P según otros autores.

   Usualmente la Cte. dieléctrica de los materiales antiferroeléctricos obedece a la ley de Curie-Weiss:

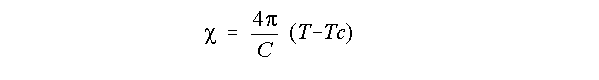
     Como la mayoría de los materiales ferroeléctricos. Experimentalmente observamos que T₀ es positivo en materiales antiferroeléctricos a diferencia de lo que sucede en el ferromagnetismo.

    Bosman y Haviga mostraron que existe una relación lineal en las cantidades de -1/C y la extrapolación de la T de Curie T_c como se muestra en la siguiente gráfica:

    Esto es muy interesante pero no se ha explicado teóricamente.

    Kittle desarrolló una teoría fenomenológica de la antiferroeléctricidad en la que mostró que no puede darse antiferroeléctricidad si T₀ es negativo.

   Hasta aquí en cuanto a lo que se refiere a la teoría fenomenológica del T.B. hay que tener en cuenta que: UNA TEORÍA FENOMENOLÓGICA IMPLICA QUE DADOS UNOS HECHOS SE DAN OTROS, PERO MÁS IMPORTANTE AÚN: DADOS UNOS HECHOS, ENTONCES OTROS DETERMINADOS NO SE PUEDEN DAR.

   ¿Donde está realmente el origen de la Ferroeléctricidad en el TB.?

   Bien, cuando estamos por encima de la temperatura de Curie. Hemos visto que la estructura es simétrica, por lo que evidentemente no vamos a tener polarización, pero cuando el TB pasa a ser Tetragonal, entonces, ¿Donde se genera la polarización? Ya tenemos una idea intuitiva. Tenemos una explicación termodinámica y fenomenológica, pero si se realiza un análisis de la estructura de la celda unidad se puede observar que la disposición simétrica que tenía la base atómica del material en la fase Cúbica Simple ha desaparecido, esto es, se puede obtener una tabla como la siguiente:

   Como podemos ver, lo que ha sucedido, es que los átomos de Oxígeno y el de Ba se han desplazado ligeramente, en la dirección de la polarización.

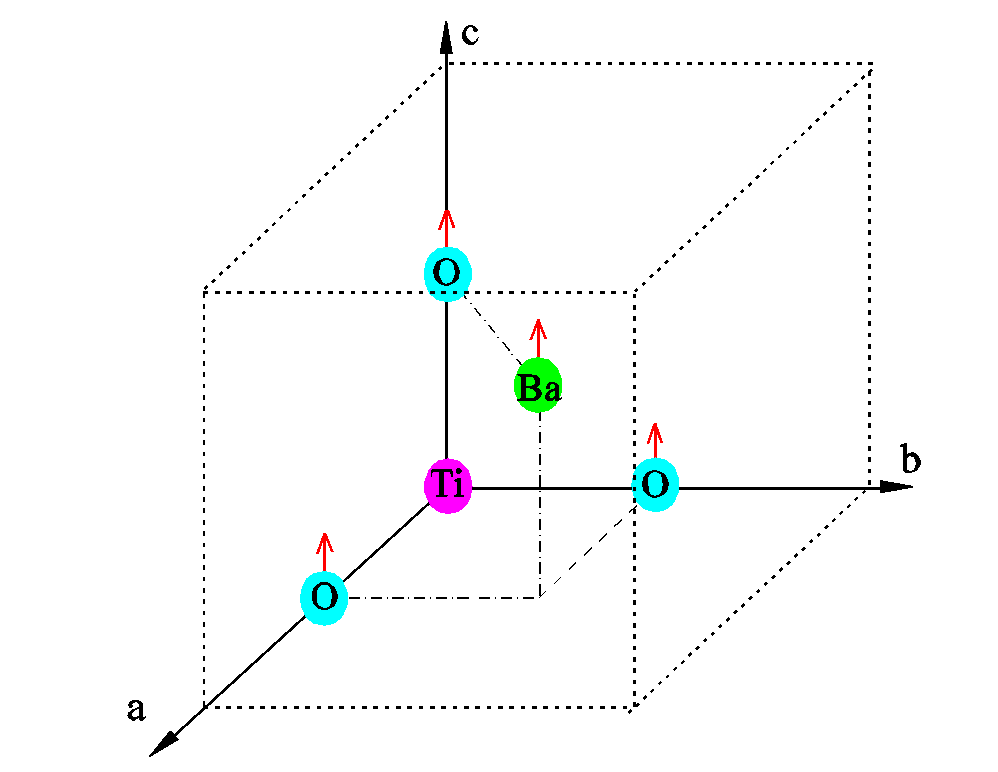
   De igual forma, cuando el TB pasa a la fase Ortorrónbica, obtenemos la tabla:

   Obsérvese, que hay representado 10 posiciones, y es que la celda unidad pasa a contener dos formulas unidad.

   Finalmente, cuando el TB pasa a la fase Romboédrica o Trigonal, obtenemos los siguientes desplazamientos:

   Que como se indica en el titulo de la tabla, se ha tomado una celda exagonal para realizar las medidas, con lo que contiene tres formulas unidad.

    En definitiva, la polarización a parece como consecuencia de un desplazamiento de la red formada por los Titanios con respecto al la red de Oxígenos y Barios. Esto se deberá a la existencia de unos mínimos de potencial para esas posiciones, que han sido explicados en otras exposiciones.

    Observese:

    Recordemos que con anterioridad se comento que las deformaciones son del orden del cuadrado de la polarización. Esto es, que pequeñas deformaciones van a generar grandes polarizaciones.

   Evidentemente, esto nos hace pensar que una presión aplicada va a generar comportamientos muy característicos.

   Como hemos dicho no existe una relación lineal entre la presión y el campo aplicado a diferencia de otros materiales.

   Si Aplicamos una presión en el plano (100) en la fase Tetragonal, debería favorecerla y así incrementar la T de Curie. Los datos experimentales, originalmente, sugieren que el incremento de la Tc es proporcional al cuadrado de la presión. Esto se puede explicar en base a la teoría fenomenológica.

   El efecto de la presión en la temperatura de Curie, Tc, es difícil de obtener de la teoría, pero el efecto de la temperatura de Curie-Weiss (T₀), puede ser determinado fácilmente. Dentro de las limitaciones usuales impuestas sobre la presión axial.

    El valor de la temperatura, puede ser determinado a partir del conocimiento de la Cte. elástica y elctrostrictiva del cristal.

    Un resultado similar es predicho por la teoría de los efectos de la presión hidrostática, para la T de Curie-Weiss.

Las medidas fueron llevados a fin por Merz en un monocristal de TB las cuales se muestran en la siguiente tabla:

     La temperatura de Curie decreció linealmente con la presión, de acuerdo con la Ec. de Claussius-Clapeyron en base a los datos de la dilatación térmica y al calor específico.

   Se encontró un buen acuerdo entre los valores teóricos y experimentales por efecto de la presión en la transición Tragonal y Ortorrombica.

nº:

Pág Siguiente,