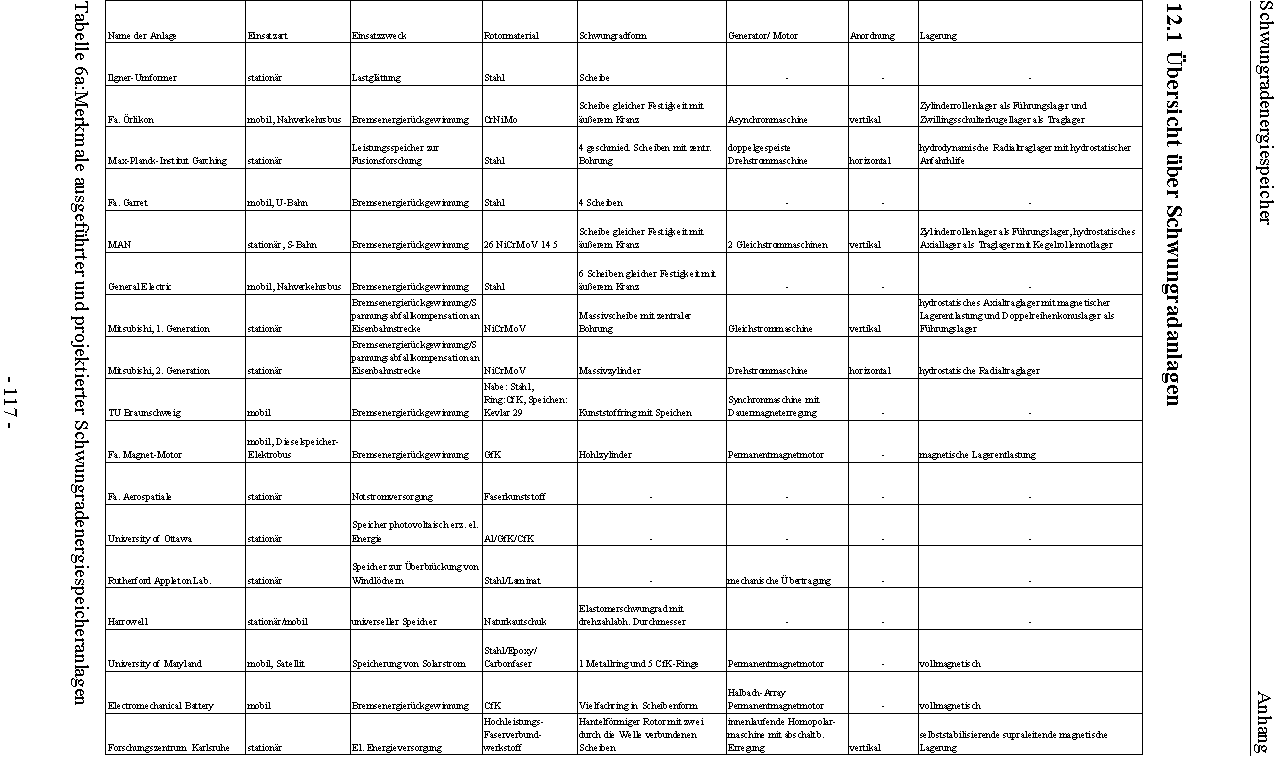
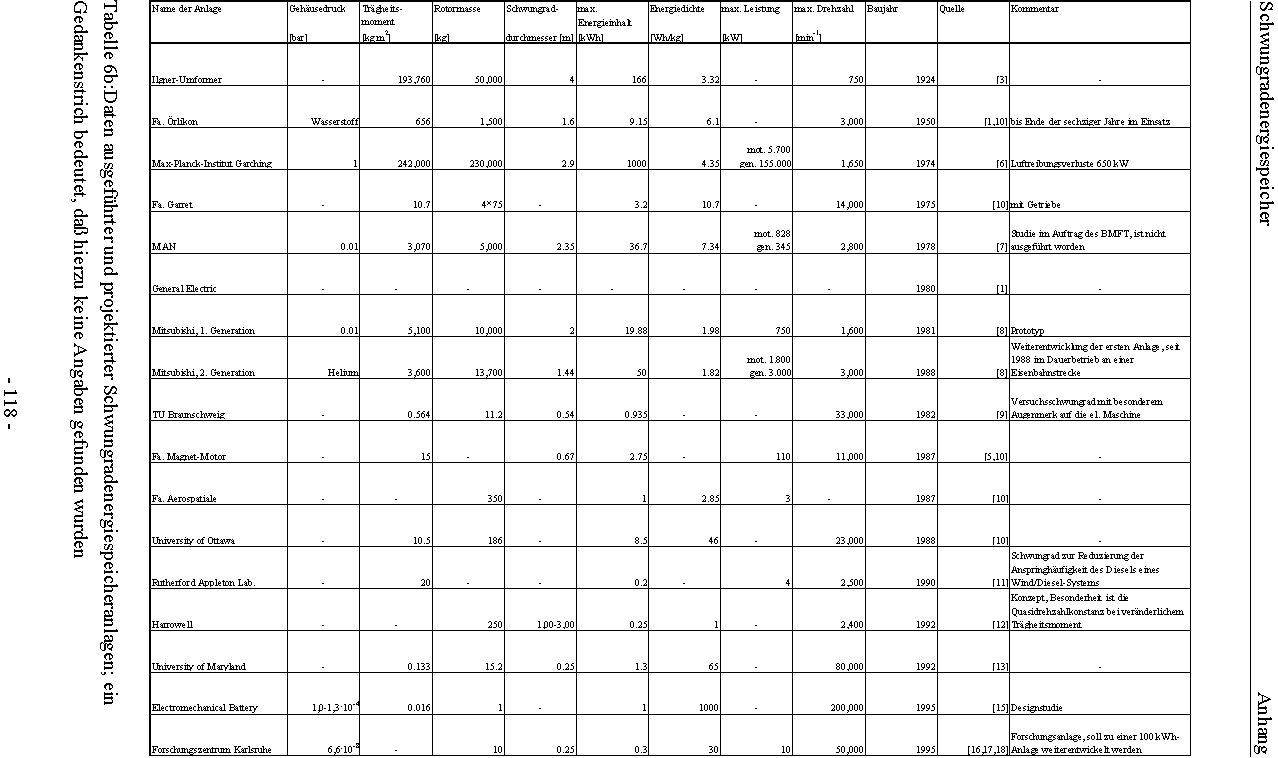
12.1 Übersicht über Schwungradanlagen
12.2 MATLAB-Programme
12.3 SIMULINK-Blöcke
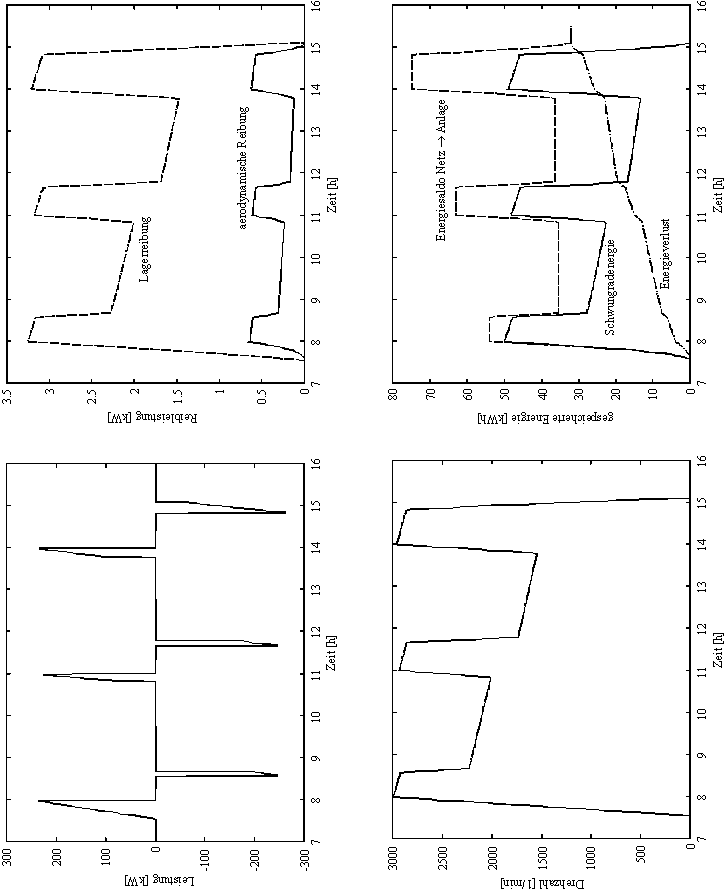
12.4 Simulationsergebnisse
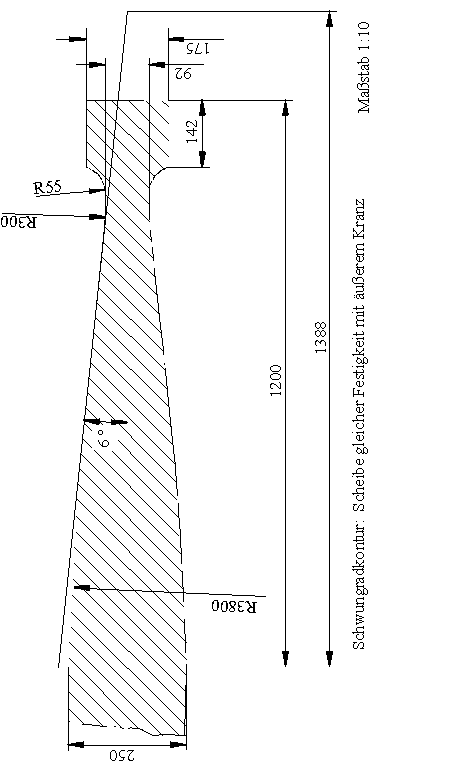
12.5 Konstruktionszeichnungen
% Programm zur Berechnung der Spannungsverteilung in einem Schwungrad mit
% beliebigem Dickenverlauf, benötigt die Kreisfrequenz und die Kontur des
% Schwungrades in Form der Vektoren r (Radius) und h (Dicke am Radius r)
% als Eingangsgrößen, wobei beide Vektoren die gleiche Länge haben müssen
% Definition des Inkrementes
dr=max(r)/100;
% Diskretisierung der Schwungradkontur
ri=0:dr:max(r);
y=interp1(r,h,ri);
bi=y/2;
ri=ri';
% Querkontraktionszahl
ny=0.3;
% Randbedingungen der Lösung I
sr1(1)=200e8; %[N/m^2] Radialspannung
st1(1)=sr1(1); % Tangentialspannung
% Berechnung der Lösung I
sr1(2)=sr1(1)+sr1(1)*(y(2)-y(1))/y(1);
st1(2)=st1(1)+ny*(sr1(2)-sr1(1));
for i=2:(length(y)-1)
sr1(i+1)=sr1(i)+(st1(i)-sr1(i)-rho*(ri(i)*omega)^2)*dr/ri(i)-...
sr1(i)*(y(i+1)-y(i))/y(i);
st1(i+1)=st1(i)+ny*(sr1(i+1)-sr1(i))-(1+ny)*(st1(i)-sr1(i))*dr/ri(i);
end
% Randbedingungen der Lösung II
sr2(1)=1;
st2(1)=1;
% Berechnung der Lösung II
sr2(2)=sr2(1)+sr2(1)*(y(2)-y(1))/y(1);
st2(2)=st2(1)+ny*(sr2(2)-sr2(1));
for i=2:(length(y)-1)
sr2(i+1)=sr2(i)+(st2(i)-sr2(i))*dr/ri(i)-sr2(i)*(y(i+1)-y(i))/y(i);
st2(i+1)=st2(i)+ny*(sr2(i+1)-sr2(i))-(1+ny)*(st2(i)-sr2(i))*dr/ri(i);
end
% Linearkombination von Lösung I und II
C=-sr1(length(y))/sr2(length(y));
sr=sr1+C*sr2;
st=st1+C*st2;
% graphische Ausgabe des Ergebnisses
% trägt die Spannungen über dem Radius auf
plot(ri,sr.*1e-6,ri,st.*1e-6)
% Programm zur Berechnung des Volumens, der Masse, des Trägheitsmomentes
% und des Formfaktors eines Schwungrades, benötigt die Kontur des
% Schwungrades in Form der Vektoren r (Radius) und h (Dicke am Radius r)
% als Eingangsgrößen, wobei beide Vektoren die gleiche Länge haben müssen
% Diskretisierung der Schwungradkontur
ii=100;
deltar=max(r)/ii;
ri=0:deltar:max(r);
h=b.*2;
hi=interp1(r,h,ri);
% Berechnung des Volumens
Vo=0;
Vu=0;
for i=1:(length(ri)-1)
Vo=Vo+(2*pi*hi(i)*(ri(i)+deltar/2)*deltar);
Vu=Vu+(2*pi*hi(i+1)*(ri(i)+deltar/2)*deltar);
end
V=(Vo+Vu)/2;
% Berechnung der Masse
rho=7860; %[kg/m^3] Dichte
m=rho*V;
% rechnet das Massenträgheitsmoment aus
Jo=0;
Ju=0;
for i=1:(length(ri)-1)
Jo=Jo+(2*pi*rho*hi(i)*(ri(i)+deltar/2)^3*deltar);
Ju=Ju+(2*pi*rho*hi(i+1)*(ri(i)+deltar/2)^3*deltar);
end
J=(Jo+Ju)/2;
% Berechnung des Formfaktors
k=0.5*J*omega^2*rho/(m*max(st));
% Ausdruck der errechneten Werte
disp([' Volumen ',num2str(V),' [m^3]'])
disp([' Masse ',num2str(m),' [kg]'])
disp([' Trägheitsmoment ',num2str(J),' [kg*m^2]'])
disp([' Formfaktor ',num2str(k),' []'])
% Programm zu Berechnung der Kontur einer Scheibe gleicher Festigkeit mit
% äußerem Kranz
sigmad=350e6; %[N/m^2] zulässige Vergleichsspannung
rho=7830; %[kg/m^3] Dichte
alpha=2.4; %[] Verhältnis von Kranzdicke zur äußeren
% Scheibendicke
ra=1.2 %[m] Außenradius
yi=0.25 %[m] Scheibendicke im Zentrum
n=3000; %[min^-1] Maximaldrehzahl
ny=0.3; %[] Querkontraktion
omega=2*pi/60*n; %[s^-1] Kreisfrequenz
% dimensionsloser Geometrieparameter
B=rho*omega^2*ra^2/(2*sigmad); %[]
% Berechnung der Kranzdimensionen nach G. Genta
% Verhältnis von Kranzinnen- zu Außendurchmesser
beta=sqrt((alpha-1+2*sqrt((alpha^2*B*(B-1+ny))/(1-ny)^2)+...
(alpha-1)^2/4)/(B*alpha)-(1+ny)/(1-ny))%[]
% äußere Scheibendicke
yd=yi*exp(-B*beta^2);
% Scheibenkontur nach Genta
r1=0:ra/1000:(beta*ra-ra/1000);
h1=yi*exp(-B*(r1/ra).^2);
r2=beta*ra:ra/1000:ra;
h2=alpha*hd*ones(size(r2));
r=[r1 r2];
% Ergebnisplot
figure(1)
b=[0.5*h1 0.5*h2];
plot(r,b,'w',r,-b,'w')
axis('equal')
hold on
% Berechnung nach Zwerenz und Schauberger
% Kranzbreite
a=(1-beta)*ra
% Kranzdicke
ya=alpha*yd/2
% Anpassungsfaktor
lambda=50
% Scheibenkontur nach Zwerenz und Schauberger
i=1000;
delta=ra/i;
r1=0:delta:ra-a-delta;
bs=(yi/2).*exp(-B.*(r1/ra).^2);
bk=(yi/2).*(ya/(yi)-exp(-B*(r1-a)/ra)).*...
(exp(lambda.*(r1/(ra-a))))/(exp(beta)-1);
b1=bs+bk;
r2=ra-a:delta:ra;
b2=(ya/2)*ones(size(r2));
r3=ra;
b3=ba;
r=[r1 r2 r3];
b=[b1 b2 b3];
% Ergebnisplot
plot(r,b,r,-b,r1,bs,r1,bk)
line([ra ra],[ya/2 -ya/2])
set(gca,'Units','centimeters','Position',[1.5 1.5 13 10],'FontName','Times-Roman','FontSize',10)
axis([0 1.3 -0.5 0.5])
figure(1)
hold
% Ausdruck der errechneten Konturparameter
disp([' Außendurchmesser ',num2str(ra),' [m]'])
disp([' Dicke/Mitte ',num2str(yi),' [m]'])
disp([' Dicke/Kranz ',num2str(ba),' [m]'])
disp([' Breite/Kranz ',num2str(a),' [m]'])
% Aufruf des Programms LOEFFLER.M zur Berechnung des tatsächlichen Spannungsverlaufes und zur graphischen Darstellung
loeffler
% Aufruf des Programms INERTIA.M zur Berechnung des Volumens, der Masse,
% des Trägheitsmomentes und des Formfaktors
inertia
function Pa = reibaero(omega)
% berechnet die aerodynamische Reibleistung eines Schwungrades,
% Eingangsgröße ist die Kreisfrequenz des Schwungrades
% Definition der Parameter
p=1e1; %[N/m^2] Gehäuseinnendruck
T=313; %[K] Temperatur
ro=1.2; %[m] Schwungradradius
Rstern=287.2; %[J/(kg*K)] Gaskonstante
m=4.782e-26; %[kg] Molekülmasse
a=3.68e-10; %[m] effektiver Moleküldurchmesser
K=1.38e-23; %[J/K] Bolzman-Konstante
% Beginn der Berechnung
n=30/pi*omega; % Schwungraddrehzahl
rho=p/(Rstern*T); % Dichte
v=sqrt((8*K*T)/(pi*m)); % Durchschnittsgeschwindigkeit der Moleküle
lambda=m/(sqrt(2)*a^2*rho*pi); % freie Weglänge der Moleküle
eta=0.5*rho*v*lambda; % dynamische Viskosität
Re=ro^2*rho*(pi/30*n)/eta; % Reynoldszahl
% Berechnung des Reibmomentes
if Re>5e4 % turbulente Strömung
Ma=0.146*rho^(4/5)*ro^(23/5)*eta^(1/5).*(pi/30.*n).^(9/5);
else % laminare Strömung
Ma=3.87*ro^4*sqrt(rho*eta*(pi/30*n).^3);
end
% Berechnung der Reibleistung
Pa=Ma*(pi/30.*n);
function Plg = reiblagr(omega)
% berechnet die Reibleistung eines Schwungrades in Abhängigkeit der
% Kreisfrequenz des Schwungrades
% Definition der Parameter
Fa=9.81*5465; %[N] Axialkraft
Fr=7.4e3; %[N] Radialkraft
% Umrechnung von Kreisfrequenz in Drehzahl
n=30/pi*omega;
% axiales Schrägkugellager in Tandemanordnung
% Parameter:
foa=4; %[] Koeffizient für die Lagerart
ny=20; %[mm^2/s] dynamische Viskosität
dma=175; %[mm] mittlerer Lagerdurchmesser
Coa=224*1e3; %[N] statische Tragzahl des Lagers
Poa=33.14*1e3; %[N] statisch äquivalente Last
% Berechnung des drehzahlabhängigen Reibmomentes
Moa=foa*1e-7*(ny*n).^(2/3)*dma^3*1e-3; %[Nm]
% Berechnung des lastabhängigen Reibmomentes
M1a=0.001*(Poa/Coa)^0.33*(1.4*Fa-0.1*Fr)*dma*1e-3; %[Nm]
% Gesamtreibmoment des Axiallagers
Ma=Moa+M1a;
% radiales Zylinderrollenlager
% Parameter:
fora=3; %[]
ny=20; %[mm^2/s]
dmr=60; %[mm]
Cor=32.5*1e3; %[N]
% Berechnung der drehzahlabhängigen Lagerlast
Por=5465*2e-5*omega.^2/2; %[N]
% Berechnung des drehzahlabhängigen Reibmomentes
Mor=fora*1e-7*(ny*n).^(2/3)*dmr^3*1e-3; %[Nm]
% Berechnung des lastabhängigen Reibmomentes
M1r=0.00025*Por*dmr*1e-3; %[Nm]
% Gesamtreibmoment des Radiallagers
Mr=Mor+M1r;
% Gesamtreibleistung der Schwungradlagerung
Plg=(Ma+Mr).*omega;