- Lebensdauer und Dauerfestigkeit
Die Lebensdauer des Schwungrades ist von der Höhe der Belastung, der Zahl der Lastspiele und den Zähigkeitseigenschaften des Materials abhängig. Es gibt mehrere Möglichkeiten der Lebensdauerbestimmung. Dazu zählen die lineare Bruchmechanik und die Berechnung nach Wöhler. Soll ein Schwungrad dauerfest ausgelegt werden, so wird bei Traupel eine Auslegungsregel vorgeschlagen, die im Turbinenbau zu Anwendung kommt. Die allgemein übliche Methode ist die Auslegung nach dem Dauerfestigkeitsschaubild, auch Smith-Diagramm genannt.
- Lineare Bruchmechanik
Zentraler Bestandteil der linearen Bruchmechanik ist die Ultraschalluntersuchung des Bauteils. Dadurch können Materialfehler im Inneren des Schwungrades entdeckt werden. Die Genauigkeit der Ultraschalluntersuchung hat jedoch ihre Grenzen, deshalb bleiben Fehler unterhalb dieser Genauigkeitsgrenze unentdeckt. Der größte, gerade nicht mehr erkennbare Fehler ist entscheidend für die lineare Bruchmechanik und heißt Ersatzfehlergröße. Es wird nun angenommen, daß sich ausgehend von diesem Fehler mit zunehmender Lastspielzahl ein Riß im Bauteil ausbreitet. Diese Rißausbreitung kann anhand von Rißfortschrittskurven mit einem analytischen Ansatz berechnet werden. Ein bekannter Ansatz ist die Formulierung der Rißausbreitungsgeschwindigkeit nach Paris [39,40]:
 (28)
(28)
a Rißlänge
N Lastspielzahl
C Werkstoffkennwert nach Paris
n doppelt logarithmische Steigung der Rißfortschrittskurve, übliche Werte für Stahl liegen zwischen 2 und 3
und mit
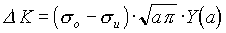 (29)
(29)
s
o,u Ober- und Unterspannung eines Lastwechsels
Y Geometriebeiwert des Risses
Wenn die Rißlänge einen bestimmten Wert übersteigt, wird die Rißausbreitung instabil, und es kommt nach wenigen weiteren Lastwechseln zu einem Bruch des Bauteils. Dieser Wert wird kritische Rißlänge ac genannt und ist wie folgt definiert:
 (30)
(30)
KIc Bruchzähigkeit
Die Ersatzfehlergröße wird unter Annahme einer ungünstigen elliptischen Fehlergeometrie in eine Anfangsrißlänge umgerechnet. Durch Integrieren der Paris-Gleichung mit der Anfangsrißlänge und der kritischen Rißlänge als Integrationsgrenzen kann man nun die Lastspielzahl errechnen, bei der die kritische Rißlänge erreicht wird. Dieses Verfahren hat den Nachteil, daß es theoretisch und mit einiger Unsicherheit behaftet ist. Auch sind die Rißfortschrittskurven und Zähigkeitswerte schwer zugänglich, da sie von der Stahlherstellern nicht veröffentlicht werden.
In der MAN-Studie ist die Lebensdauer nach der linearen Bruchmechanik berechnet worden. Als Material für das MAN-Schwungrad war der Vergütungsstahl 26 NiCrMoV 14 5 vorgesehen. Dieser Stahl besitzt eine Streckgrenze von 700 N/mm2. Die Lebensdauer dieses Schwungrades wurde mit Hilfe der linearen Bruchmechanik zu 14 Jahren berechnet. Dabei wurde eine Ultraschall-Ersatzfehlergröße von 2 mm und eine Zykluszahl von 1,125·106 angenommen.
Die maximal zulässige Spannung lag bei 258 N/mm2. Somit ergibt sich ein Verhältnis von maximaler Spannung zur Streckgrenze von 0,37. Auf die Streckgrenze von 30 CrNiMo 8 von 1050 N/mm2 übertragen, würde dies eine maximale Spannung von 387 N/mm2 bedeuten. Das hier auszulegende Schwungrad wird gemäß dem hypothetischen Lastzyklus zur Maximumüberwachung mit drei Zyklen pro Arbeitstag belastet. Nach 20 Jahren hätte das Schwungrad also 15600 Zyklen erfahren.
- Wöhlerlinie
Ein mehr praxisorientiertes Verfahren ist die Lebensdauerbestimmung nach Wöhler.

Bild 28: Wöhlerkurve mit Spannungskollektiv
In einem Einstufen-Versuch wird die jeweilige Bruchlastspielzahl in Abhängigkeit von der Ausschlagsspannung experimentell ermittelt. Die Ausschlagsspannung wird so lange herabgesetzt, bis Bruchlastspielzahlen im Bereich von 0,5-1·106 erreicht werden. Belastungen, deren Bruchlastspielzahlen oberhalb von 0,5-1·106 liegen, nennt man dauerfest. Man erhält die Wöhlerlinie durch Auftragen der Ergebnisse in einem doppelt-logarithmischen Diagramm.
Wirkt nun in einer realen Belastung statt einer konstanten Ausschlagsspannung im Einstufenversuch ein Beanspruchungskollektiv mit ständig wechselnder Ausschlagsspannung auf das Bauteil, geht die rechnerische Lebensdauervorhersage nach Wöhler auch von einem linearem Schädigungszuwachs aus.
Nach der von Palmgren und Miner aufgestellten Hypothese kommt es bei jedem Schwingspiel, dessen Spannungsausschlag oberhalb der Dauerfestigkeit liegt, zu einer Teilschädigung 1/Ni, wenn Ni die Bruchlastspielzahl der Wöhlerkurve für diesen Spannungsausschlag ist. Bei einem Beanspruchungskollektiv werden die einzelnen Teilschädigungen aufsummiert:
 (31)
(31)
Das Versagen eines Bauteils tritt ein, wenn die Schadenssumme gleich eins wird. Da diese Vorhersage jedoch mit einer großen Unsicherheit behaftet ist, werden Schadenssummen von S = 0,3 zur Vordimensionierung empfohlen [39].
Für die Zugänglichkeit von Wöhlerkurven gilt dasselbe wie für die lineare Bruchmechanik, es ließ sich keine Literatur über quantitative Wöhlerkurven für die verschieden Stahlsorten finden. Auch eine diesbezügliche Nachfrage im Institut für Werkstoffkunde blieb ohne Erfolg [38]. Man kann sich jedoch aus der Zugfestigkeit und der Streckgrenze eine synthetische Wöhlerlinie berechnen. Dieses Berechnungsverfahren stützt sich auf eine statistische Auswertung einer großen Anzahl von Wöhlerlinien. Nähere Informationen finden sich in [41].
- Verfahren nach Traupel
Die Berechnung nach Traupel ist für Turbinenläufer entwickelt worden und ist keine Lebensdauerberechnung, sondern eine Auslegungshilfe. Die Berechnung besagt, daß die maximale Drehzahl einer rotierenden Scheibe erreicht ist, wenn die Streckgrenze im gesamten Bauteil erreicht ist. Diese Drehzahl läßt sich anhand der Geometrie und der Streckgrenze des Materials bestimmen. Die Auslegungsregel besagt nun, daß die maximale Drehzahl ungefähr 1,5-mal größer als die Betriebsdrehzahl sein soll. Damit kann man die sichere Betriebsdrehzahl errechnen [42]. Diese Methode eignet sich aber nur für einen iterativen Auslegungsprozeß, da die Geometrie wiederum von der zulässigen Höchstdrehzahl abhängig ist.
- Dauerfestigkeitsschaubild
Das in Bild 29 dargestellte Dauerfestigkeitsschaubild ist in seinen äußeren Umrissen [39] entnommen. Es erfolgte anschließend eine Reduktion mit dem Größenbeiwert b1 und dem Oberflächenbeiwert b2. Somit erhält man das Gestaltdauerfestigkeitsschaubild. Da bei einer Überlastung des Bauteils sowohl die Ausschlagsspannung sVa als auch die Mittelspannung sVm ansteigen, muß die Sicherheit gegen Erreichen der Grenzoberspannung sGo gleich der Sicherheit gegen Erreichen der Grenzausschlagsspannung sGa sein. Mit einer Sicherheit von S = 2 ergibt sich somit aus dem Gestaltdauerfestigkeitsschaubild eine Vergleichsoberspannung von 332 N
/mm2.

Bild 29: Gestaltdauerfestigkeitsschaubild von 30 CrNiMo 8 bei Zugbeanspruchung
- Zulässige Materialbelastung
Da keine Wöhlerkurven bzw. Rißfortschrittskurven und Bruchzähigkeitswerte für die Lebensdauerberechnung verfügbar waren, und aus Zeitgründen eine Berechnung einer synthetischen Wöhlerlinie nicht mehr möglich war, wird die zulässige Vergleichsspannung anhand der Berechnung der MAN-Studie und des Gestaltdauerfestigkeitsschaubildes festgelegt. Nach ersterer wäre eine Vergleichsspannung von 387 N/mm2 und nach letzterer eine Vergleichsspannung von 332 N/mm2 angebracht. Bezieht man die Unsicherheiten beider Berechnungen mit ein, liegt man bei einer Vergleichsspannung von 350 N/mm2 in einem realistischen Bereich. Dieser Wert ist, wie oben schon erwähnt, ein Schätzwert und bedarf bei einer endgültigen Auslegung einer sorgfältigeren Berechnung.
- Festigkeitsberechnung
Bei der Festigkeitsberechnung von Schwungrädern geht man in der Regel von einem zweiachsigen, achsensymmetrischen Hauptspannungszustand aus. Das Schwungrad dreht mit konstanter Drehzahl, so daß kein Moment in axialer Richtung wirkt. Die Normalspannungen in axialer Richtung und daraus resultierende Schubspannungen werden vernachlässigt. Diese Annahme ist nur gültig, wenn die Dicke eines Schwungrades klein gegenüber dem Radius ist. Es wird weiterhin angenommen, daß die Temperatur im gesamten Schwungrad konstant ist.

Bild 30: Gleichgewichtsbetrachtung am Element einer rotierenden Scheibe mit beliebiger Form
Das in Bild 30 gezeigte Raumelement erfährt somit aufgrund seiner Masse dm und der Rotation eine Fliehkraft dZ:
 (32)
(32)
w
Kreisfrequenz
r Radius
y(r) Scheibendicke
j
Zentriwinkel
r
Dichte
Die Tangentialspannungen bewirken eine Kraftkomponente R am Raumelement in radialer Richtung (siehe Krafteck in Bild 30):
 (33)
(33)
Das Kräftegleichgewicht in radialer Richtung ergibt sich somit zu:
 (34)
(34)
Durch Differentiation gelangt man schließlich zur folgenden Form:
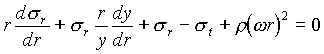 (35)
(35)
s
r Radialspannung
s
t Tangentialspannung
Zusätzlich zum Kräftegleichgewicht werden die Zusammenhänge zwischen Spannungen und Verformungen über das Hook´sche Gesetz in radialer und tangentialer Richtung ausgedrückt:
 (36)
(36)
 (37)
(37)
e
r Dehnung in radialer Richtung
e
t Dehnung in tangentialer Richtung
E Elastizitätsmodul
n
Querkontraktionszahl
v örtliche Radialverschiebung
Die Gleichung (37) wird nach r abgeleitet und in die Gleichung (36) eingesetzt:
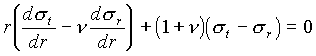 (38)
(38)
Die Gleichungen (35) und (38) bilden ein Differentialgleichungssystem. Anhand dieses Systems kann bei gegebener Form des Schwungrades y(r) die Spannungsverteilung berechnet werden. Es ist aber auch möglich, eine Spannungsverteilung vorzugeben und dann die Form des Schwungrades zu bestimmen.
- Scheibe gleicher Dicke
Die einfachste Schwungradform ist die Scheibe gleicher Dicke. Hierfür gilt die Bedingung:
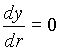 (39)
(39)
Die Gleichung (35) wird hiermit vereinfacht, nach s
t aufgelöst und in die Gleichung (38) eingesetzt. Es ergibt sich eine lineare Differentialgleichung zweiter Ordnung in s
r:
 (40)
(40)
Die Lösung dieser Differentialgleichung hängt davon ab, ob die Scheibe ein zentrales Loch besitzt oder nicht. Bei einer Scheibe mit zentralem Loch erhält man mit der Randbedingung, daß die Radialspannungen am Außen- und Innenrand der Scheibe null sind, folgende Radialspannungsverteilung:
 (41)
(41)
mit b
= ri /ra
c
= r /ra
Die Tangentialspannungsverteilung erhält man durch Einsetzen von Gleichung (41) in Gleichung (35):
 (42)
(42)
Mit b
= 0 ergibt sich die Lösung für die Scheibe konstanter Dicke ohne zentrales Loch:
 (43)
(43)
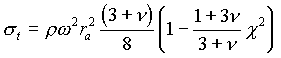 (44)
(44)
Bei einem Vergleich der Lösungen für die Scheibe mit und ohne Loch fällt auf, daß die Spannungsverläufe für die Scheibe mit Loch für b ®
0 nicht identisch mit denen für die Scheibe ohne Loch sind. Die maximalen Spannungen in tangentialer Richtung treten am inneren Rand bzw. in der Scheibenmitte auf:
 , mit Loch und b ®
0 (45)
, mit Loch und b ®
0 (45)
 , ohne Loch (46)
, ohne Loch (46)
Die maximale Spannung der Scheibe mit Loch ist also doppelt so hoch wie die maximale Spannung der Scheibe ohne Loch. Dieses wird auch aus dem Bild 30 deutlich:

Bild 31: Spannungsverteilung in einer Scheibe konstanter Dicke
Hierin sind die dimensionslosen Spannungen sr,t/rw2ra2 in Abhängigkeit von dem Verhältnis von Innenradius zu Außenradius b über den relativen Radius c aufgetragen. Die Spannungsverläufe für b ®
0 nähern sich immer mehr dem Verlauf für b = 0 an, spreizen sich aber in unmittelbarer Nähe des Innenrandes auseinander. Das bedeutet, daß eine noch so kleine Bohrung eine Verdoppelung der Tangentialspannung zur Folge hat, weshalb durchgehende Bohrungen zur Befestigung der Wellenflansche vermieden werden sollen. Bei der Scheibe ohne Loch sind die Tangential- und Radialspannungen maximal und einander gleich, nämlich 0,4125 rw2ra2.
- Scheibe gleicher Festigkeit
Die einfachste Lösung des aus den Gleichungen (35) und (38) gebildeten Differentialgleichungssystems ist die Scheibe gleicher Festigkeit, die bereits im letzen Jahrhundert von de Laval hergeleitet wurde. Es wird angenommen, daß innerhalb der Scheibe die Tangential- und die Radialspannung einander gleich sind:
 (47)
(47)
Damit fällt die Gleichung (38) weg und die Gleichung (35) vereinfacht sich zu:
 (48)
(48)
Diese Differentialgleichung hat die einfache Lösung:
 (49)
(49)
mit 
yi Scheibendicke im Zentrum

Bild 32: Kontur der Scheibe gleicher Festigkeit in Abhängigkeit von B
Im Bild 32 ist der Verlauf der relativen Dicke dimensionslos über den relativen Radius aufgetragen. Zunehmende Werte von B bedeuten dabei eine Zunahme des Produktes von Kreisfrequenz und äußerem Radius. Die Voraussetzung für die Scheibe gleicher Festigkeit ist nur erfüllt, wenn auch am äußeren Rand Radialspannung und Tangentialspannung gleich sind. Die Radialspannung ist aber am äußeren Rand null. Daher muß eine Radialspannung am äußeren Rand erzeugt werden.
Man erreicht dies durch einen Kranz, der so bemessen ist, daß seine Radial- und Tangentialspannung an seinem Innenrand gleich der Spannung innerhalb der idealen Scheibe gleicher Festigkeit ist. Der Kranz ist dabei dicker als die Scheibe an ihrem Außenrand. Um die Spannungskonzentration zu vermindern, die durch die sprunghafte Dickenänderung entsteht, wird die Scheibendicke mit Hilfe einer Korrekturkurve sanft an den Kranz angepaßt.

Bild 33: Geometrische Definition der Scheibe gleicher Festigkeit
Bei Genta [1] wird für die näherungsweise Bestimmung der Kranzdimensionen folgende Formel herangezogen:

(50)
Durch den Parameter B (siehe Gleichung (49)) sind die maximale Spannung, die Dichte, der Außenradius und die Drehzahl vorgegeben. Wählt man ein beliebiges Verhältnis von Kranzdicke zu Scheibendicke am Außenrand a, so erhält man aus Gleichung (50) das Verhältnis von Scheibenradius zu Gesamtradius b, und die Abmessungen des Kranzes sind festgelegt. Nun muß noch eine Funktion gefunden werden, die den Sprung der Scheibendicke entschärft. Genta hat dafür eine Arkustangensfunktion vorgeschlagen, deren Wendepunkt bei rD liegt, eleganter ist aber eine aus Exponentialfunktionen gebildete Korrekturkurve, die von Zwerenz und Schauberger [7] benutzt wurde. Diese soll in leicht abgewandelter Form auch in dieser Arbeit zur Anwendung kommen.
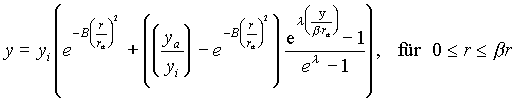 (51)
(51)
Scheibe gl. Festigkeit Korrekturkurve
Für kleine Werte von r dominiert der erste Teil der Gleichung (51). Wenn die Werte von r in die Nähe von bra kommen, steigt der zweite Teil der Gleichung rasch an, bis schließlich für r = bra die Scheibendicke y gleich der Kranzdicke ya wird. Der Parameter l bestimmt, wie sanft die Scheibenkontur an den Kranz angepaßt wird. Kleine Werte von l sorgen für einen sanfteren, größere Werte für einen härteren Übergang.
- Numerisches Verfahren nach Löffler
Die hier vorgestellten Lösungen sind nur Sonderfälle von Scheibenformen. Will man die Spannungen in einer Scheibe beliebiger Form berechnen, so ist eine Lösung des aus den Gleichungen (35) und (38) gebildeten Gleichungssystems nicht mehr analytisch möglich. Als der Computer noch keinen Einzug in die Ingenieurwissenschaft gehalten hatte, setzte man Scheiben beliebiger Form aus kegeligen Teilringen zusammen, für die wiederum geschlossene Lösungen existieren (Verfahren nach Keller und Salzmann [42]).
Mit Hilfe des Computers kann man das Differentialgleichungssystem auch numerisch lösen. Wandelt man das Differentialgleichungssystem in Differenzengleichungen um, so kann man mit wenig Rechenaufwand die Spannungsverläufe berechnen:
 (52)
(52)
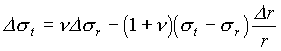 (53)
(53)
Dieses Verfahren nach Löffler [42] eignet sich für Scheiben mit zentralem Loch und ohne zentrales Loch. Je kleiner die Schrittweite Dr ist, desto genauer ist auch die Lösung. An dieser Stelle soll das Verfahren anhand einer Scheibe ohne Loch beschrieben werden. Bei einer ersten Lösung der Differenzengleichungen werden die Spannungen im Zentrum zu sr(0) = sr(0) = s beliebig gewählt. Nun löst man ausgehend vom Zentrum die Differenzengleichungen für jeden Schritt Dr und erhält die Spannungen srI und stI an der Stelle r + Dr zu
s(r + Dr) =s(r) + Ds . Dann setzt man w = 0 und sr(0) = sr(0) = 1 und berechnet die Lösungen srII und stII . Die gesuchte Gesamtlösung ergibt sich aus einer Linearkombination von Lösung I und II :
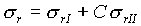 (54)
(54)
 (55)
(55)
Die unbekannte Konstante C wird aus der Grenzbedingung für die Radialspannung am Außenrand berechnet.
 (56)
(56)
Somit ist die Spannungsverteilung über die gesamte Scheibe bestimmt.
Es ist zu erwähnen, daß die hier aufgeführten Lösungen auf der Annahme des ebenen Spannungszustandes basieren.
Sowohl bei der Scheibe gleicher Dicke als auch bei der Scheibe gleicher Festigkeit sind die größten Tangential- und Radialspannung einander gleich. Axialspannungen und Schubspannungen treten definitionsgemäß nicht auf. Die Vergleichsspannung an den Stellen maximaler Belastung ist daher gleich der Tangential- oder Radialspannung, unabhängig davon, ob die Vergleichsspannung mit der Normalspannungs-, der Schubspannungs- oder der Gestaltänderungsenergie-Hypothese ermittelt worden ist.
Die Annahme des ebenen Spannungszustandes ist aber nur erlaubt, wenn das Verhältnis von Scheibendicke zu Scheibenradius hinreichend klein und die Steigung der Scheibenkontur hinreichend flach ist. Bei einer Scheibe gleicher Festigkeit mit B = 1,23 (siehe Gleichung (49)) und yi/ra = 0,22 ist die maximale Spannung in tangentialer Richtung bei einer dreidimensionalen Berechnung 5 % größer als mit der Annahme des ebenen Spannungszustandes. Die maximale Axialspannung beträgt ca. 10 % der Auslegungsspannung. Wird die Gestaltenergieänderungs-Hypothese angewendet, so wird die Auslegungsspannung schon bei einer um 6 % reduzierten Drehzahl erreicht [1]. Dieses macht deutlich, daß die hier beschriebenen Lösungen nur für eine Vorauslegung geeignet sind und unbedingt mit einer Finite-Elemente-Berechnung
überprüft werden müssen.
- Schwungradform
Nach den vorhergehenden theoretischen Überlegungen sollen nun die für dieses Projekt am besten geeignete Schwungradform und die Schwungradabmessungen festgelegt werden.

|
Linienart |
Formfaktor |
Masse [kg] |
Mtm J [kgm 2] |
Drehzahl [min -1] |
Radius [mm] |
Dicke [mm] |
|
durchgezogen |
0,77 |
5465 |
3668 |
3000 |
1200 |
250 |
|
strichpunktiert |
0,606 |
6922 |
3668 |
3000 |
1033 |
260 |
|
gestrichelt |
0,606 |
6922 |
4984 |
2566 |
1200 |
190 |
Bild 34: Daten von drei Schwungrädern mit 50 kWh Energieinhalt
Dazu wurden die oben aufgeführten formelmäßigen Zusammenhänge in den MATLAB-Programmen LOEFFLER.M und KONTUR.M zusammengefaßt und verschiedene Schwungradformen berechnet.
Im Bild 34 sind die Konturen von drei Schwungrädern abgebildet, die einen Energieinhalt von 50 kWh besitzen und deren maximale Spannung 336 N/mm2 beträgt. Das durchgezogen gezeichnete Schwungrad ist als Scheibe gleicher Festigkeit nach Gleichung (51) mit folgenden Parametern berechnet worden:
yi = 250 mm, ya = 175 mm, ra = 1200 mm, B = 1.59, b = 0,88 und l = 50.
Der Vergleich der beiden Scheiben gleicher Dicke zeigt, daß eine dünnere Scheibe mit größerem Radius bei gleicher Masse langsamer dreht als eine dickere mit kleinerem Radius. Das bedeutet für die dünnere Scheibe, daß die Lagerreibung geringer, die Luftreibung aber größer ist. Da die Luftreibung durch den Unterdruck um einiges kleiner ist als die Lagerreibung, ist eine dünnere Scheibe zu bevorzugen. Allerdings steigt mit zunehmendem Radius die Belastung des Gehäuses durch den Druckunterschied quadratisch an, so daß hier ein Kompromiß zwischen Reibungsarmut und Aufwand für das Gehäuse gefunden werden muß.
Es ist zu erkennen, daß die Scheibe gleicher Festigkeit um ca. 1,5 t leichter als die Scheibe gleicher Dicke ist. Mit der Scheibe gleicher Dicke können also Materialkosten gespart und die Lagerreibung verringert werden.
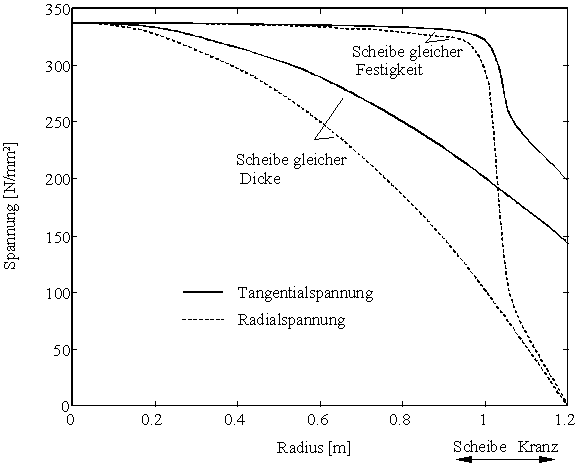
Bild 35: Spannungsverlauf in der Scheibe gleicher Dicke und gleicher Festigkeit
Im Bild 35 sind die mit dem Verfahren nach Löffler errechneten Spannungen in den beiden Scheiben gleichen Durchmessers über den Radius aufgetragen. Die Voraussetzung für die Scheibe gleicher Festigkeit, daß Tangential- und Radialspannung gleich groß und konstant über den Radius sind, kann bis in Kranznähe sehr gut erfüllt werden. Die maximale Spannung tritt im Scheibenzentrum auf und weicht von der Auslegungsspannung nur um 14 N/mm2 ab.
Die Drehzahl von 3000 min-1 ist nicht ungewöhnlich für große Stahlscheiben. Für Dampfturbinenläufer ist dies die Standarddrehzahl, so daß genügend Erfahrungen mit der Fliehkraftbelastung und der Materialermüdung vorhanden sind. Die Belastung von Schwungrädern ist zudem geringer, da die thermische Belastung entfällt. Auch für den elektrischen Anlagenteil ist ein Drehstrom im Bereich von 16,6-50 Hz und die Umrichtung auf die Netzfrequenz von 50 Hz ein gängiger Bereich.
Daher wird die Scheibe gleicher Festigkeit mit den obigen Daten für die weitere Konstruktion gewählt.
- Anordnung des Schwungrades

 (28)
(28) (30)
(30)
 (31)
(31)

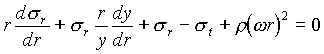 (
( (
( (37)
(37)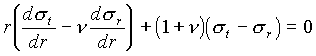 (
(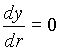 (39)
(39) (40)
(40) (41)
(41) (42)
(42) (43)
(43)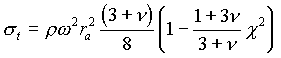 (44)
(44) , mit Loch und b ®
0 (45)
, mit Loch und b ®
0 (45) , ohne Loch (46)
, ohne Loch (46)
 (48)
(48) (
(


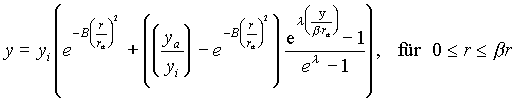 (51)
(51)
 (52)
(52)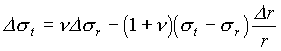 (53)
(53) (56)
(56)
