5. Schwungrad als Energiespeicher

1. Energiefluß

Um die im Schwungrad bei der Energiespeicherung und -entnahme stattfindenden Vorgänge zu verdeutlichen, wird zunächst nur das mechanische System betrachtet und der Drallsatz für das reibungsfrei laufende Schwungrad mit konstantem Massenträgheitsmoment aufgestellt:



Bild 14: Prinzipbild der Energiespeicherung

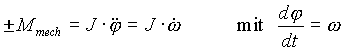(8)

mechanisches Moment der Welle

J Massenträgheitsmoment

w Winkelgeschwindigkeit

j Drehwinkel

 

Ist das mechanische Moment positiv, so wird das Schwungrad beschleunigt, es wird Energie eingespeichert. Umgekehrt wird bei einem negativen Moment dem Schwungrad Energie entzogen. Die dabei erbrachte mechanische Leistung ist proportional zur Winkelgeschwindigkeit und zum Moment:

(9)

Pmech mechanische Leistung

 

Die während eines Zeitraums t2 - t1 gespeicherte bzw. entnommene Energie ergibt sich aus der Integration der Leistung über diesen Zeitraum und ist bekanntermaßen abhängig vom Massenträgheitsmoment und von der Winkelgeschwindigkeit, mit der es rotiert:

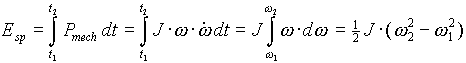(10)

Esp gespeicherte bzw. entnommene Energie

 

Im Betrieb unterliegt die Schwungradanlage mehreren Beschränkungen. Zum einem darf die maximale Drehzahl nicht überschritten werden, da sonst das Schwungradmaterial zu stark durch die Fliehkraft belastet würde und es zu einem Materialversagen des Schwungrades käme. Diese Drehzahlgrenze wird durch die Forderung nach einer langen Schwungradlebensdauer noch weiter herabgesetzt. Zum anderen ist die maximale Leistungszufuhr und -abgabe durch den elektrischen Anlagenteil und die Schwungradwelle eingeschränkt.

Bei der elektrischen Maschine unterscheidet man zwischen einer Kurzzeitbelastung und einer Dauerbelastung, wobei die Kurzzeitbelastung weit höher als die Dauerbelastung sein kann. Ausschlaggebend für die Belastungsgrenze ist der durch die Maschinenströme hervorgerufene Temperaturanstieg, der zu einer Schädigung der Wicklungsisolierungen führt. Weiterhin ist das von der Maschine und der Schwungradwelle übertragbare Moment leistungsbegrenzend. Im folgenden Bild sind die Begrenzungen im Fall der Leistungsaufnahme des Schwungrades schematisch dargestellt:



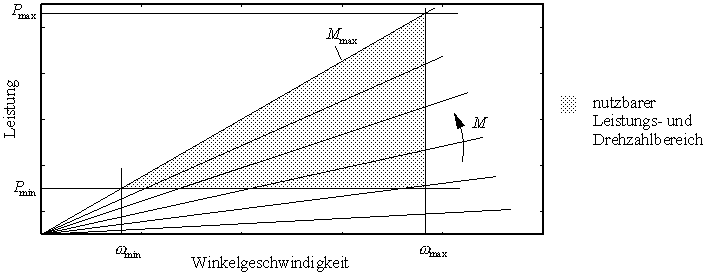
Bild 15: Begrenzungen bei der Leistungsaufnahme

Die strahlenförmig auseinandergehenden Geraden geben den linearen Zusammenhang zwischen Leistung und Winkelgeschwindigkeit nach Gleichung (9) mit dem Moment als Parameter wieder. Die größte mögliche Steigung ist demnach bei maximalen Moment gegeben. Soll das Schwungrad im Arbeitsbereich stets eine Mindestleistung zu Verfügung stellen können, so muß die Drehzahl auch nach unten begrenzt werden. Die Grenze ergibt sich aus dem Quotienten aus der Mindestleistung und dem maximal zulässigen Moment.

Ist der elektrische Anlagenteil entsprechend groß dimensioniert, kann man dem Schwungrad nach Gleichung (9) eine beliebig hohe Leistung entnehmen oder zuführen. Man bezeichnet daher einen Schwungradenergiespeicher auch als "Leistungsspeicher", auch wenn dies formal nicht korrekt ist, da man eine Leistung nicht speichern kann. Es wird allerdings bei niedrigen Drehzahlen zunehmend schwieriger, dem Schwungrad Energie zuzuführen und zu entnehmen.

2. Verluste

Das oben betrachtete mechanische System ist unvollständig, da außer dem von der elektrischen Maschine erzeugten Moment noch weitere durch Reibung hervorgerufene Momente auf das Schwungrad wirken. Die Lagerreibung erzeugt ein Lagerreibmoment MLager, das von der Lagerbelastung und der Drehzahl abhängig ist. Ebenso entsteht durch Luftreibung an dem Schwungrad ein von Drehzahl und Gehäuseinnendruck abhängiges Reibmoment Maero. Wenn die elektrische Maschine außerhalb des Gehäuses angebracht ist, kommt noch das drehzahlabhängige Dichtungsreibmoment MDicht hinzu. Mit diesen zusätzlichen Momenten ändert sich der Drallsatz nach Gleichung (8) wie folgt:

(11)

Diese Gleichung wird mit der Winkelgeschwindigkeit erweitert und man erhält die Differentialgleichung für die Energiespeicherung im reibungsbehafteten Schwungrad:

(12)

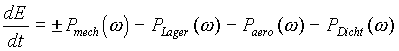
Die Schwungradanlage besitzt zudem einige Hilfsaggregate, die eine Versorgungsleistung PHilf benötigen. Zu den Hilfsaggregaten zählen je nach Bedarf der Steuerschrank, eine Niederdruckpumpe für die Ölschmierung und Kühlung bei Wälzlagerung, eine Hochdruckpumpe zur Druckölversorgung und Wärmeabfuhr bei hydrostatischer Lagerung, die Gleichstromversorgung der Elektromagnete bei magnetischer Lagerung, eine Vakuumpumpe für die Gehäuseevakuierung, die abhängig von der Dichtigkeit des Gehäuses auch nur im intermittierenden Betrieb laufen kann, und eine Kühleinrichtung für die elektrische Maschine.



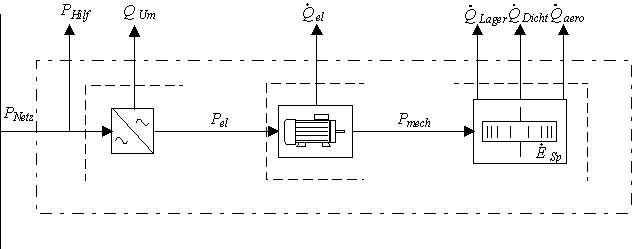
Bild 16: Leistungsfluß in der Schwungradspeicheranlage beim Laden

Im elektrischen Anlagenteil wird beim Laden die aus dem Drehstromnetz entnommene elektrische Leistung PNetz in die mechanische Leistung der Schwungradwelle umgewandelt. Zuerst wird die Versorgungsleistung der Hilfsaggregate von der Netzleistung abgeführt. Die Umwandlung der Netzleistung in die mechanische Wellenleistung ist verlustbehaftet, und der Leistungsfluß kann aus einer Leistungsbilanz um die elektrische Maschine und den Umrichter erhalten werden:

(13)

Bei der Umwandlung der Netzleistung in die mechanische Wellenleistung entstehen in der elektrischen Maschine und im Umrichter Verluste, die sich im Maschinenwirkungsgrad h el,L und im Umrichterwirkungsgrad h Um,L für den Ladevorgang ausdrücken lassen:

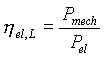(14)

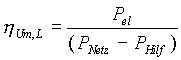(15)

Die Gleichungen (14) und (15) werden nun in die Gleichung (12) eingesetzt, und man erhält den Zusammenhang zwischen der Änderung der Speicherenergie und der aus dem Netz entnommenen Leistung während des Ladevorgangs:

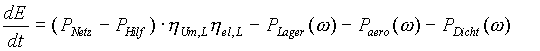(16)



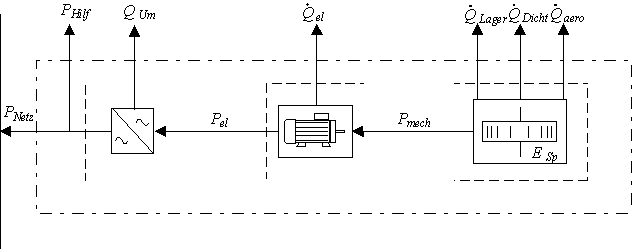
Bild 17: Leistungsfluß in der Schwungradspeicheranlage beim Entladen

Betrachtet man nun den Entladevorgang der Schwungradanlage, so kehrt sich der Leistungsfluß im elektrischen Anlagenteil um. Der Maschinenwirkungsgrad h el,E und der Umrichterwirkungsgrad h Um,E für den Entladevorgang ergibt sich zu:

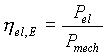(17)

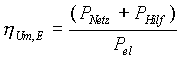(18)

In die Gleichung (12) eingesetzt, ergibt sich somit der Zusammenhang zwischen der Änderung der eingespeicherten Energie und der ins Netz eingespeisten Leistung:

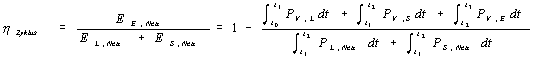(19)

Die innerhalb des Schwungradgehäuses, in der elektrischen Maschine und im Umrichter auftretenden Verlustleistungen wandeln sich vollständig in Wärme um, die über die Wärmeströme Verlust an die Umgebung abgeführt werden.

3. Wirkungsgrad und Speichergüte

Der Wirkungsgrad der Schwungradenergiespeicheranlage ist von der jeweiligen Betriebsart abhängig. Allgemein ist der Wirkungsgrad als Quotient aus Nutzen zu Aufwand definiert. Da sich die Verlustleistungen mit der Drehzahl ändern, müssen sie über die Zeit aufintegriert werden. Der Wirkungsgrad wird daher mit den Energiedifferenzen gebildet. In der folgenden Abbildung werden der Schwungradenergieinhalt und der Energiesaldo zwischen dem Netz und der gesamten Anlage während eines Speicherzyklus dargestellt:



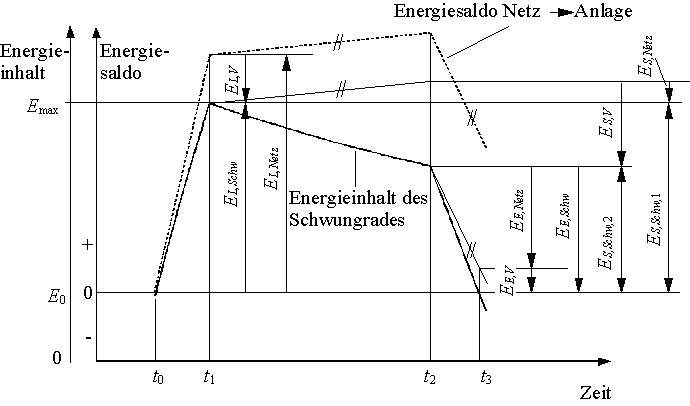
Bild 18: Energieinhalt eines schematischen Speicherzyklus

Beim Ladevorgang ist der Nutzen die Zunahme der Schwungradrotationsenergie EL,Schw und der Aufwand die aus dem Netz entnommene elektrische Energie EL,Netz während des Zeitraumes t1 - t0. Dabei wird die Energie EL,V als Wärme an die Umgebung abgegeben. Der Ladewirkungsgrad ist daher nach Gleichung (9) (im folgenden werden die Wirkungsgrade von Umrichter und Maschine für Lade- und Entladevorgang als gleich angenommen):

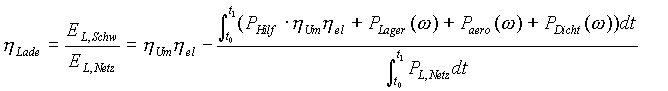(20)

Während der Speicherung wird das Schwungrad durch die Reibung im mechanischen Anlagenteil abgebremst. Dabei kommt die Leerlaufverlustleistung der Maschine PM,Leer als zusätzliche Verlustleistung in der Bilanz hinzu. Es fließt keine elektrische Energie vom Netz in das Schwungrad. Trotzdem wird die zur Versorgung der Hilfsaggregate notwendige Leistung PHilf aus dem Netz entnommen, und der Energiesaldo steigt. Die zum Zeitpunkt t2 übriggebliebene Rotationsenergie ES,Schw,2 ist als Nutzen und die zum Zeitpunkt t1 im Schwungrad eingespeicherte Energie zuzüglich der aus dem Netz entnommenen Energie ES,Netz ist als Aufwand anzusehen:

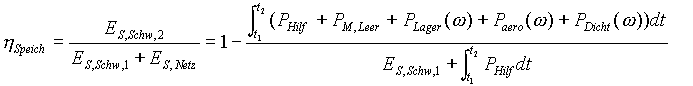(21)

Beim Entladevorgang ist der Nutzen die an das Netz abgegebene elektrische Energie EE,Netz und der Aufwand die Abnahme des Schwungradenergieinhaltes EE,Schw. Der Entladewirkungsgrad ergibt sich zu:

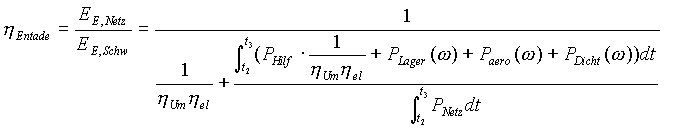(22)

Schließlich läßt sich formal auch noch ein Zykluswirkungsgrad aufstellen, in dem die zum Ende des Zyklus an das Netz abgegebene elektrische Energie EE,Netz ins Verhältnis zur der während des gesamten Zyklus von Netz aufgenommenen Energie EL,Netz + ES,Netz gesetzt wird.

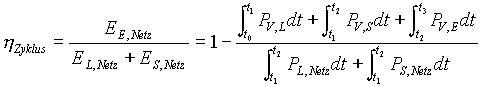(23)

Aus der formelmäßigen Betrachtung der hier hergeleiteten Wirkungsgrade lassen sich folgende Schlüsse ziehen:

· Werden die mechanischen Verlustleistungen und die Leistung für die Hilfsantriebe vernachlässigt, so ist der beste erreichbare Wirkungsgrad beim Laden und Entladen jeweils gleich dem Produkt aus Umrichter- und Maschinenwirkungsgrad.

· Der beste erreichbare Zykluswirkungsgrad ist unter Vernachlässigung der mechanischen Verlustleistungen gleich dem Produkt aus Umrichter- und Maschinenwirkungsgrad zum Quadrat.

· Bei einem reibungsbehafteten Schwungradsystem ist der Wirkungsgrad bei Aufladung und Entladung auf hohem Niveau, das heißt bei einem großen Verhältnis von Netzleistung zu Verlustleistung, günstiger als auf niedrigem Niveau.

· Der Wirkungsgrad ist wegen der Reibleistungen bei niedrigen Drehzahlen besser als bei hohen Drehzahlen.

· Der Speicher- und der Zykluswirkungsgrad sind abhängig vom gewählten Zyklus und können daher für ein- und dieselbe Schwungradanlage bei verschiedenen Fahrweisen völlig unterschiedlich sein.

Der Speicher- und der Zykluswirkungsgrad eignen sich daher nicht als zyklusunabhängige Vergleichsgrößen für die Speichergüte einer Anlage. Das nächste Bild zeigt qualitativ die Abnahme des Energieinhaltes von zwei unterschiedlichen Schwungrädern, nachdem die äußere Energiezufuhr eingestellt worden ist.



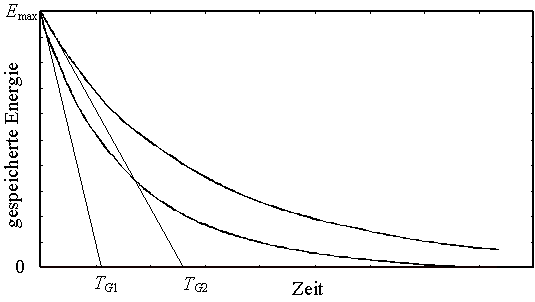
Bild 19: Auslaufkurven von zwei unterschiedlichen Schwungrädern gleichen Energieinhalts

Die Steigung der Auslaufkurve ist zu jedem Zeitpunkt gleich der Verlustleistung des Schwungrades. In [22] wird nun die Speichergüte als Quotient aus dem maximalem Energieinhalt (in kWh) und der Verlustleistung (in kW) bei maximaler Drehzahl definiert:

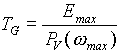(24)

Die Speichergüte TG hat die Dimension einer Zeit und entspricht der theoretischen Zeitdauer in Stunden, in der ein Schwungrad bei konstanter Verlustleistung zum Stillstand kommen würde. Die Speichergüte ist somit allein eine Eigenschaft des mechanischen Teils einer Schwungradanlage, und man kann damit verschiedene Schwungräder bezüglich ihrer Verluste zyklusunabhängig vergleichen.

4. Speicherstrategien

Die vorangegangenen Überlegungen machen deutlich, daß ein Einsatz von Schwungrädern als Energiespeicher nur bei gewissen Arbeitszyklen oder Aufgaben sinnvoll sein kann.

Bei einem Betrieb, bei dem ein aufgeladenes Schwungrad sich solange dreht, bis ein zufällig eintretendes Ereignis den Entladevorgang auslöst, kann es dazu führen, daß der Zykluswirkungsgrad negativ wird. Das heißt, die Verlustenergie wird größer als die zu Beginn des Zyklus eingespeicherte Energie. Ein zur Notstromversorgung eingesetztes Schwungrad kann trotzdem wirtschaftlich sein, wenn der wirtschaftliche Nutzen einer Sofortreserve z.B. die Verhinderung von Datenverlusten bei Computern oder die Vermeidung von Schäden an empfindlichen technischen Einrichtungen ist, und die dadurch vermiedenen Kosten größer als die Kosten für die Deckung der ständigen Verlustleistung sind. Ein als reiner Energiespeicher arbeitendes Schwungrad kann weder wirtschaftlich noch energieeffizient bei zufälligen Speicherfällen eingesetzt werden.

Im exakt vorherbestimmten Speicherfall ist selbst eine Anlage mit hohen Speicherverlusten sinnvoll, da man hier das Schwungrad unmittelbar nach dem Aufladen auch wieder entladen kann. Ein Beispiel hierfür ist die Garchinger Schwungradanlage [6].

Der sinnvollste Einsatzbereich für Schwungradenergiespeicher sind die zyklisch auftretenden Speicherfälle, bei denen sich jeder einzelne Zyklus in bezug auf Speicherbedarf und Speicherdauer unterschiedlich verhält. Es ist jedoch statistisch ein mittlerer Bedarf ermittelbar, für den der Speicher ausgelegt wird. Um einen sinnvollen Speichereinsatz zu gewährleisten, sollte daher die Laufzeit im aufgeladenen Zustand so kurz wie möglich sein, und die Energieeinspeicherung und Entladung sollte bei hohen Leistungen stattfinden.