Abstract

A brief analysis on the perfect reconstruction theory of 2- channel filter bank using polyphase representation. It is found that the down sampling does not introduce aliasing or any other distortion in the reconstruction process but rather it avoids the redundancy factor. The perfect reconstruction is solely dependent on the analysis and synthesis filters. We can arrive at the same aliasing-free perfect reconstruction condition without using down-sampling and up-sampling scheme. Theoretically it is much simpler, and also the filters satisfying this condition can also be used in the 2-channel filter bank scheme using down-sampling and up-sampling scheme to achieve perfect reconstruction.

Introduction

A 2-channel filter bank is the foundation for the subband coding. It’s still being used in various applications of signal processing. Its importance has increased tremendously with the advent of multi-resolution concept. The popularity of 2- channel filter bank is because of its ability to achieve perfect reconstruction using QMF filter and hence is also popularly known as QMF bank. It was first introduced by Crosier et al,[ 2] in mid nineties, since then it has been a good topics of many researchers. It has been used in the multi-resolution analysis, for the compression and coding of speech and images. We will study here basically the perfect reconstructibilty issue of 2-channel filter bank and some interesting theoretical aspects.

A single stage 2-channel filter bank consists of analysis and synthesis parts. In the analysis part, a signal is first decomposed into two sub-sampled signals and using two analysis filters and followed by decimation by a factor of 2 as shown in figure 1.a.

In the synthesis part, the signal is reconstructed back from its decomposed components. To reconstruct the signal from its decomposed or sub-sampled signal and , these two components are first up-sampled by 2, which are then passed through two synthesis filters and to produce the reconstructed signal. It is usually assumed that the reconstructed signal may suffer three major distortions, aliasing, amplitude and phase distortion. The perfect reconstruction of the signal lies in the elimination of these three distortion such that the reconstructed signal becomes the exact replica of the original.

For 2-channel case it was in Crosier, et al[2] aliasing can be completely eliminated by a simple choice of synthesis filters. Smith and Barnwell [4] and Mintzer [3] showed that all the three distortions can be eliminated with properly designed FIR filters. But we will see later that in actual practice no aliasing term appears in the reconstruction.

Perfect reconstruction theory in 2-Channel filter bank

We will produce here briefly the existing perfect reconstruction using polyphase representation. The decomposed components and in figure-1 are represented as

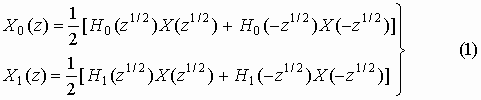
Coming to the synthesis part, the reconstructed signal is usually expressed as

Expanding and rearranging, we can write the reconstructed signal as

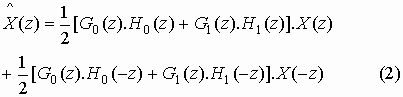
The second term is assumed to be aliasing component. Its removal is necessary to reconstruct the signal . This can be achieved by putting the second term in the equation (2) zero. That

then equation (2) becomes

Equation (3) can be modified as

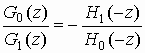
These equations can be satisfied in four ways.

Case-1: When , then 

Equation (3) is satisfied easily by this choice. But we can’t take this choice because the right hand side of equation (4) becomes zero. That is, we can’t reconstruct with this choice even if we can eliminate the aliasing terms altogather.

Case-2: When , then 

For the same reasoning as in case-1, we can’t go for this option. We have two more options to satisfy equation (3).

Case-3: When , then 

We can make both equation (3) and (4) satisfied, this leads to conjugate Quadrature Mirror Filter.

Case-4: When , then 

This choice of filters leads to the Quadrature Mirror Filter. Removing the aliasing term is not the only condition for reconstructing the original signal from its decomposed parts, we have to impose one more condition in equation (4). That is,

Where is the delay factor and c is some constant.

If we can find analysis and synthesis filters that satisfy equation (5), we can decompose a signal using the analysis filters and get back the signal from its decomposed components using the reconstruction filters.

Irrelevancy of Aliasing term

Let us briefly analyze the role of aliasing term in perfect reconstruction. In actual practice, aliasing term is removed before reconstruction, it  can be anything and will have no role in the perfect reconstruction. For example, we can write equation (2) as

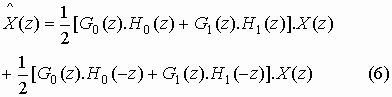
Equation (6) does not disturb the equation (3), (4) and (5). Or even we can write,

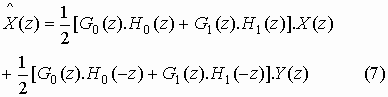
This expression also does not disturb the equation (3), (4) and (5). This clearly shows that the concept of aliasing terms in 2-channel filter bank is irrelevant and hence nothing to do with the perfect reconstruction.

Aliasing-free Reconstruction Scheme

From the above reconstruction scheme, we know that our main aim is to obtain equation (4) in any case. If we can obtain equation (4), under any circumstance and then it would be possible to obtain the original signal, provided we could find analysis and synthesis filters satisfying equation (5).

We can directly obtain equation (4) using the following structure in Figure-2.

We decompose the signal  into and using the same two analysis filters and . That is,

In the synthesis part, we reconstruct the signal using the synthesis filters and . That is,

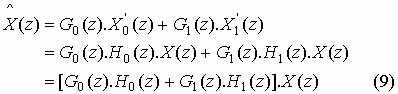
Equation (9) is the same as equation (4), except the factor ½ . This shows that, if we can find the analysis and synthesis filters such that equation (5) is satisfied, then we would be able to perfect reconstruction in the figure-2 as we get perfect reconstruction as in figure-1. But the reconstruction scheme based on figure-2 is much simpler as it involves no aliasing term. There is no reason to say that figure-2 of reconstruction scheme is wrong in z-domain.

The question now is, is figure-2 true in time domain also? If the figure-2 is true in z-domain, it should also be true in time domain. Converting the equation (9) in time domain we can write

That is, if we can find and such that

where c is some constant and is the delay factor, then we would be able to get perfect reconstruction.

This clearly shows that equation (3) has nothing to do with the perfect reconstruction. Equation (5) or (9) is sufficient condition for perfect reconstruction, nothing more is required.

Practical Examples

We have practically found that we can get perfect reconstruction from both the filter bank schemes of figure-1 and figure-2, using the filters obtained from equation (11).

Let , ,

and be the analysis and synthesis filters. They satisfy equation (11) since

.

In other words

Let be a sequence of length 8. Then from the figure-2, we have

That is,

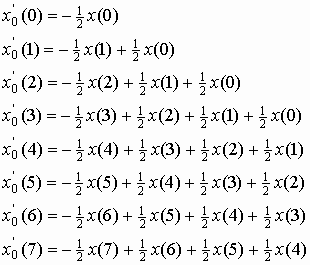
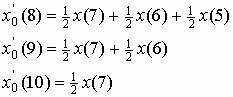
and

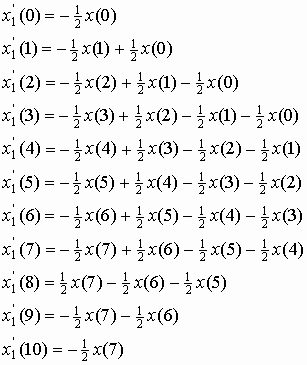
then the reconstructed signal is

substituting the values of and in the above equation (12), we get

Thus we can obtain the sequence by multiplying the reconstructed signal with ½.

In case of figure-1, we have

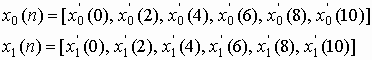
and corresponding up-sampled components are

Then we have

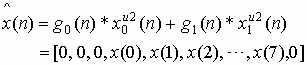
Thus we can get the perfect reconstruction from the figure-1 also using the filters that satisfy equation (11). This consolidates the claim that aliasing does not occur in the down-sampling process of figure-1. In other words, equation (3) has no role in the perfect reconstruction process.

Discussion and Remarks

We have discussed the perfect reconstruction theory of 2-channel filter bank. And it is found that the aliasing term has no role in reconstruction. It is introduced just to make the perfect reconstruction theory more complex, as we can arrive at the same perfect reconstruction relation without introducing the aliasing term. The irrelevancy of aliasing terms in 2-channel perfect reconstruction theory is also proved clearly. We then arrive at the reconstruction scheme of figure-2, which preserves the perfect reconstruction condition without aliasing terms. The time domain version of the condition of perfect reconstruction is then provided in equation (11). We have also shown with practical examples that we can achieve perfect reconstruction without imposing any condition to cancel aliasing term. This clearly shows that aliasing does not occur in down sampling. From this discussion, it is also clear that perfect reconstruction can be achieved without down sampling. Down sampling is only to remove the redundancy factor in the signal reconstruction. In our example, the reconstructed signal becomes 2 times of the original signal if we reconstruct without down sampling. The reconstruction of the signal can be achieved either by retaining odd components or even components of in each of the analysis filter output. This does not introduce any kind of distortion contrary to what most of the signal processing experts believe. This can be easily from our example of reconstruction in time domain.

Conclusion

Aliasing term in the perfect reconstruction theory of 2-channel filter bank is a fictitious term, it does not occur because of the down sampling and hence we need not concern for it. This term appears only in theory because of the polyphase representation of the down-sampled components in z-domain and makes the theory of perfect reconstruction unnecessarily complex. This questions the suitability of the polyphase representation in expressing analysis and synthesis filter bank.

References

[1] A.N. Akansu, R.A. Hadad, Multiresolution Signal Decomposition. Boston: Academic Press, 1992

[2] Crochiere R. E., Webber S.A., and Flanagan J.L. "Digital Coding of Speech in Subbands," Bell System. Tech, J., Vol-55, pp. 1069-1085, Oct. 1976

[3] F. Mintzer ,"Filters for Distortion-free Two Band Filter Banks", IEEE Trans. ASSP, Vol-ASSP-33, pp. 626-630, June 1985.

[4] M.J.T.Smith, T.P. Barnwell III, "A Procedure for Designing Exact Reconstruction Filter Banks for Tree-structured Subband Coders", Proc. IEEE Int. Conf.Acoust. Speech and Signal Proc., pp. 27.1.1-27.1.4, San Diego, CA, March 1984.

[5] M. Vetterli, "Filter Banks Allowing for Perfect Recostruction", Signal Processing, Vol-10., pp. 219-244, April 1986.

[6] M. Vetterli, D. Le Gall, "Perfect Reconstruction FIR Filter Banks: Some Properties and Factorizations", IEEE ASSP, Vol-ASSP-37, pp. 1057-1071, July 1989.

[7] N.J. Fliege, Mutirate Signal Processing, Accademic Press, 1992.

[8] P.P. Vaidyanathan, "Quadrature Mirror Filter Banks, M-Band Extensions and Perfect Reconstruction Techniques",IEEE ASSP megazine, Vol-4, pp. 4-20,July 1987.

[9] P.P. Vaidyanathan. Multirate Systems and Filter Banks., Englewood Cliffs: Prentice Hall,

1993

[10] V.K. Jain and R.E. Crochiere, " Quadrature Mirror Filter Design in Time Domain", IEEE Trans. ASSP, Vol-ASSP-32, pp. 353-361, April 1984.