Criteria For Perfect
Reconstructiblity of Filters of QMF Types.
Yumnam Kirani Singh
& Swapan Kumar Parui
Indian Statistical
Institute,
Computer Vision &
Pattern Recognition Unit.
203 B.T. Road,
Cal-35, India
email: kiranisingh@hotmail.com, skp@www.isical.ac.in
Abstract:
Prefect reconstructibility is the
main criteria for all transforms. In the case of wavelets and filter bank, we
used two filters for decomposition and two filters for reconstruction process.
Any set of such four filters, which can be used for decomposition and the
perfect reconstruction process is called a perfectly reconstructible filter
(PRF) set. We propose here new
criteria for finding the decomposition and reconstruction filters from a set of
real numbers. Following the trend of ISITRA, any set of real numbers, which
satisfies the criteria is a member of a PRF set. And all other members of the
PRF can be obtained from it using the QMF rule. Once a filter is found out, it
can be used for finding different sets of PRF. We describe how the sets of
perfectly reconstructible filter can be obtained easily using our new criteria
being proposed here.
1. Introduction
Perfect reconstruction is an
important issue for transforms. Transforms, such as FFT, DCT, GHT, GWT, etc are
perfectly reconstructible from their decomposed components. In the case of
wavelets and filter bank, we used two filters for decomposition and two filters
for reconstruction process. We will call any set of filters, which can be used
for decomposition and perfect reconstruction, a perfectly reconstructible
filter set. In the case of wavelets,
there are wavelets, where perfect reconstruction is not possible from their
decomposed components. Maxican Hat wavelet, Meyer Wavelets belong to such
wavelets. The perfectly reconstructible wavelets are those compactly supported
wavelets constructed or proposed by Daubechies. Because of their perfect
reconstructible properties, DB wavelets are commonly used in various
applications. In short, inversibility and practical utility has direct
relation. The main theoretical background of wavelets and filter banks is also
to find those PRF sets. In order to find a PRF, we have to know the clue what
makes perfectly Db-wavelet filter perfectly reconstructible? What are the main
criteria for wavelets or filter banks to be perfectly reconstructible? We will
address this problem mainly.
Different researchers in the
fields of wavelets and filter-banks have done a lot of works in searching the
criteria for perfect reconstructiblity. The work of Croiser and Esteban [1],
proposal of QMF, is worth mentioning. It helps us in finding other members of a
PRF set in an easier way if we know a member of it. But nothing was mentioned
about how to know that a set of real numbers will be a member of PRF set.
Daubechies,[2],[3] has also done remarkable works on this and established a
relation known as admissibility condition based on Fourier transform on the
possibility of perfect reconstruction of a wavelet. According to Daubechies,
for a wavelet to be inversible or perfectly reconstructible, the wavelet has to
satisfy the admissibility condition. Testing admissibility condition for a new
wavelet is not an easy task and hence finding a wavelet that satisfies the
admissibility condition is still a problem. We propose here new criteria, which
can be used in general for testing whether a particular set of real number can
be a member of a PRF set. These criteria were derived based on using Bino’s
Model of Multiplication [5], [6] in a section of ISITRA-1. Once a member of PRF
is found out, we can easily find the other members of PRF using QMF rule. But
QMF is not the only criteria for a perfect reconstruction to be made possible. That
means we can have different sets of decomposition and reconstruction filters,
which does not satisfy the QMF criteria yet make the perfect reconstruction
possible. Many other possible ways of producing perfectly reconstructible
filter sets are studied in ISITRA [7]. Here we discuss only those PRF sets of
QMF types, as the commonly used compactly supported Db-wavelet filters are of
QMF types. We also discuss why perfect reconstruction is possible in the case
of DB wavelets and some cases of filter banks on the basis of our newly found
criteria.
This paper is mainly aimed at the
introduction of flexibility of ISITRA-1 in finding filter coefficients. We give
here equations required for finding filter coefficients as well as equations
for doing decomposition and reconstruction using those filters. Also to show
the various possibilities of PRF sets once a filter is found out, some tables
are provided as well for different length of filters. The paper is divided into
four sections. Section 2 gives the formulations and procedures of finding
filter coefficients of first few filters of even lengths. Section 3 gives the
generalization of the problem. Some examples are also given for better
understanding of readers in section 2 and 3. An elaborate discussion is given in
section 4 and conclusion in section 5.
2. PRF of first few even
lengths.
2.1 Filter of length 2:
We know in FIR filters, the
components of filters are real numbers. The same is true for wavelet filters.
The question here is how to choose those real numbers for filter coefficients.
In the case of wavelets and filter coefficients, a signal is decomposed into an
approximation and a detail component using two decomposition filters. Then it
is reconstructed using two reconstruction filters. Thus we require four filters
in the decomposition and the reconstruction process. In the case of ISITRA, a
signal is decomposed into two components 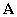 and
and 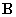 , not necessarily into an approximation and a detail.
Following the trend of ISITRA, we will denote the decomposition filters by
, not necessarily into an approximation and a detail.
Following the trend of ISITRA, we will denote the decomposition filters by  and
and 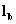 and the
reconstruction filters respectively by
and the
reconstruction filters respectively by 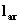 and
and  . The set of these four filters will be known as perfectly
reconstructible filter of length 2 (PRF2) set in the rest part of the paper.
. The set of these four filters will be known as perfectly
reconstructible filter of length 2 (PRF2) set in the rest part of the paper.
Let  be a discrete signal and
be a discrete signal and  and
and  , be any two decomposition filters of length 2, where
, be any two decomposition filters of length 2, where  and
and  are any two real
numbers. Then using Bino’s Model of Multiplication, we can write,
are any two real
numbers. Then using Bino’s Model of Multiplication, we can write,
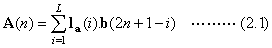
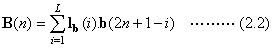
where  is the length of the
filter and
is the length of the
filter and  .
.
Thus, 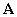 and
and  are the decomposed components of
are the decomposed components of 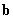
The above two equations gives the
decomposed components of the signal filtered using  and
and 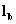 . The corresponding filters components for reconstruction of
the signal from
. The corresponding filters components for reconstruction of
the signal from 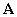 and
and  are the mirror image of the corresponding filters, i.e.,
are the mirror image of the corresponding filters, i.e., 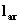 is the mirror image of
is the mirror image of  and
and  is the mirror image of
is the mirror image of 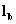 . Thus we have,
. Thus we have,  and
and  as the reconstruction
filters. Finally, we can reconstruct back the original signal
as the reconstruction
filters. Finally, we can reconstruct back the original signal 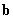 from its decomposed components
from its decomposed components 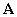 and
and  using the following relations
using the following relations


where  and m, the length of
the signal.
and m, the length of
the signal.
Equation (2.3) gives the odd
values and equation (2.4), the even values of the signal 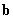 . We have put no restriction on the value of the two elements of the vector of the PRF2 set, which means that any non-zero real vector of length 2 can be a member of PRF2 set.
. We have put no restriction on the value of the two elements of the vector of the PRF2 set, which means that any non-zero real vector of length 2 can be a member of PRF2 set.
Thus we can see that any non zero real vector of length 2 can be used as a filter for perfect reconstruction. Haar’s Wavelet is perfectly reconstructible, because it is also a vector of length 2. We don’t bother about orthonormalization of vectors, because that is always possible. So, instead of thinking and using Haar’s wavelet for analysis of different signals, we can use any two real numbers of our choice and use it for our analysis purpose. Moreover, the role of decomposition and the reconstruction filters can be interchanged. That means, we can decompose a signal using reconstruction filter sets and then reconstruct using decomposition filters. Which way we perform decomposition and reconstruction depends on the problem of the application.
How to find members of the
PRF2 set?
For choosing decomposition and
reconstruction filters, we proceed as follows
- Find any vector of non-zero vector of length 2. This
is one of the decomposition filters (say
 ).
).
- Change the sign in the vector in such a way that the
element-wise multiplication of the vector you chose and the new vector
results in alternate changes in sign. Then reverse the vector. This gives
you another decomposition filter
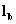 .
.
- Find the vector whose elements are the mirror images
of the elements of the vector in step 1. This gives you the reconstruction
filter
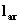 corresponding to the decomposition filter
corresponding to the decomposition filter  .
.
- Similarly find the mirror image of the
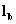 , which will give you the reconstruction filter
, which will give you the reconstruction filter  .
.
Example-1. If we choose  then we find
then we find  or
or 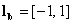 , according to step 2. And the corresponding reconstruction filters are
, according to step 2. And the corresponding reconstruction filters are  and
and  or
or 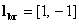 . Once we get the decomposition filters, we can use it for decomposing any signal using equations (2.1) and (2.2). And after some processing operations are done on the transformed data, they are used for reconstruction of the signal using the corresponding reconstruction filters.
. Once we get the decomposition filters, we can use it for decomposing any signal using equations (2.1) and (2.2). And after some processing operations are done on the transformed data, they are used for reconstruction of the signal using the corresponding reconstruction filters.
Example-2. The DB1’s wavelet
filters are  ,
,  ,
,  and
and  .
.
Thus we see that any vector of
length 2 can be used for the generation of the perfectly reconstructible filter
set. Thus choosing becomes much more interesting fun than ever.
2.2 Filter of length 4:
In the case of filters of length
2, we see that any non-zero real vector can be a member of PRF2 set. Is it
possible for any non-zero vector of length 4 too? That is, can any vector of
length 4 be a member of PRF4 set? The answer is no. For a non-zero real vector
of length 4 to be a member of PRF4 set, it has to satisfy the following
condition.
Member condition:
- The product of the 1st and the 3rd
elements of the vector should be equal in magnitude but opposite in sign
to the product of the 2nd and the 4th elements of
the vector.
Mathematically, if  is a non-zero real vector of length 4, then to be member of PRF4 set, it should satisfy the following relation.
is a non-zero real vector of length 4, then to be member of PRF4 set, it should satisfy the following relation.
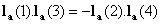
Any vector, which satisfies the
above condition, can be used for the generation of a perfectly reconstructible
filter set.
Exampe-1: The low pass decomposition filter of Db-2 wavelet (of length 4) satisfies the above two conditions. Let’s take the elements of the low pass filter up to four decimal places only. Then  satisfies the above two conditions, as the elements of
satisfies the above two conditions, as the elements of
 are not of same sign and
are not of same sign and
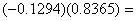 -0.1082
-0.1082
 0.1082,
0.1082,
i.e., (1).
(1).  (3)= -
(3)= -  (2).
(2).  (4)
(4)
So,  can be used for the
generation of the perfectly reconstructible filter set. The process of finding the other three filters of the set from
can be used for the
generation of the perfectly reconstructible filter set. The process of finding the other three filters of the set from  is similar to that of finding
is similar to that of finding
 ,
, and
and  from
from  in the case of length 2 filters in the previous section.
in the case of length 2 filters in the previous section.
Let 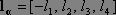 be a vector such that
be a vector such that  , then as usual we get,
, then as usual we get, 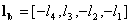
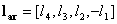 and
and 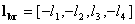 . These four filters are said to be QMF in terms of filter
bank and wavelets, but in our case these four filters are said to form a
perfectly reconstructible set. Once we get such a filter set, then we can decompose
a discrete signal,
. These four filters are said to be QMF in terms of filter
bank and wavelets, but in our case these four filters are said to form a
perfectly reconstructible set. Once we get such a filter set, then we can decompose
a discrete signal, , into two parts substituting the filters or vectors
, into two parts substituting the filters or vectors  and
and 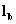 in the following relations.
in the following relations.


where  is the length of the corresponding filter and
is the length of the corresponding filter and  +1.
+1.
The two decomposed components
indeed correspond to the approximation and the detail parts of the signal.
The reconstruction of the
original signal from these decomposed components using the corresponding
reconstruction filters 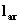 and
and  involves the following steps. For simplicity and ease of
computation, let’s define the following
involves the following steps. For simplicity and ease of
computation, let’s define the following

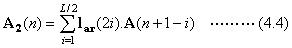

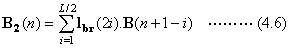
Once we get the above four terms,
from the Model of ISITRA, then the reconstruction of the original is
straightforward and is given by the following two equations.

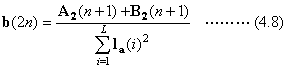
Equation (4.7) gives the odd
values and equation (4.8), the even values of the original signal.
A few PRF sets of length 4 are
given in table-1.
Thus once we can find a vector 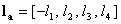 that satisfies the condition
that satisfies the condition 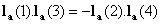 , then we can find a number of filter sets as in the table-1.
As in the case of length 2 filters, the role of decomposition and
reconstruction filter sets can be interchanged.
, then we can find a number of filter sets as in the table-1.
As in the case of length 2 filters, the role of decomposition and
reconstruction filter sets can be interchanged.
How to find the member of PRF4
set?
- Choose any two real numbers and let it be your
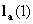 and
and  .
.
- Choose another real number as your
 , and then find
, and then find  from the relation
from the relation 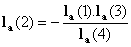 .
.
- Find
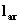 from the relation,
from the relation,  =
= 
- Find
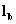 from the relation,
from the relation, 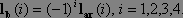
- Then find
 from the relation,
from the relation, 
Thus finding a PRF4 set here,
following the concept of ISITRA, is much simpler than the finding of any
reconstructible filter set from wavelets.
2.3 Filter of length 6:
We have seen how to find the
coefficients of a filter of length 2 and length 4. In the case of length 2
filters, any non-zero vector of length 2 can be used as a filter. But in the
case of length 4, that were not as simple as in case of length 2 filters. For a
non-zero real vector of the length 4 to
be a member of PRF4 set, it has to satisfy an important condition that, the
product of the 1st and the 3rd elements should be equal
in magnitude but opposite in sign to the product of the 2nd and the
4th elements of the vector. In the case of filter of length 6, what
are the conditions to be satisfied by a vector to be a member of PRF6 set?In case of filter of length 6, it has to satisfy following two conditions to be a member of perfectly reconstructible
filter set.
Let  be a vector of length 6. Then it should satisfy the following
two conditions to be member of perfectly reconstructible filter (PRF6) set.
be a vector of length 6. Then it should satisfy the following
two conditions to be member of perfectly reconstructible filter (PRF6) set.
Member condition:
Condition 1:
Condition 2: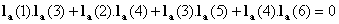
Any vector of length 6 which
satisfy the above two conditions is a member of PRF6 set. Once we find a member
of PRF6 set, then we can find the other filters in the set as in the usual way.
A few PRF6 sets are given in table-2.
The PRF set of length 6 are not
limited to the 12 sets given in table-2. One may find more PRF6 sets that
satisfy the condition 1 and 2. Once we find a PRF6 set, we can use equation
(4.1) and (4.2) for decomposition of a signal, with 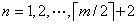 . And the original signal can be reconstructed from equations
(4.7) and (4.8) by substituting the denominator index by
. And the original signal can be reconstructed from equations
(4.7) and (4.8) by substituting the denominator index by 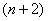 in place of
in place of  . Once a non-zero real vector for a filter is obtained, we
can find a number of PRF6 set from it by arranging the elements of the filter
in different ways. This flexibility is not mentioned in the case of wavelet
filters and filter banks.
. Once a non-zero real vector for a filter is obtained, we
can find a number of PRF6 set from it by arranging the elements of the filter
in different ways. This flexibility is not mentioned in the case of wavelet
filters and filter banks.
How to find the members of a PRF6
set?
- From the condition 1, find
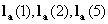 and
and  as finding a member of in PRF4 set.
as finding a member of in PRF4 set.
- Substitute the values of
 and
and  in condition 2 and find the values
in condition 2 and find the values  for different values of
for different values of  . Thus we find
. Thus we find  , a member of PRF6 set.
, a member of PRF6 set.
- Find
 from the relation,
from the relation, 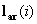 =
= 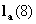
- Find
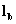 from the relation,
from the relation, 
- Then find
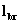 from the relation,
from the relation, 
2.4 Filters of length 8:
We know, for a set of real
numbers of even length greater than 2, to be a member of a PRF of corresponding
length, it has to satisfy the member conditions. The same is true for a member
of PRF8. The following three conditions are to be satisfied by a non-zero real
vector  of length 8 to be a member of PRF8.
of length 8 to be a member of PRF8.
Member Condition:
Condition 1: 
Condition 2: 
Condition 3: 
Any vector of length 8, which
satisfies the above three conditions is a member of PRF8 and other members can
be found out from it as usual. The table-3 gives some of the PRF8 sets.
How to find the members of a
PRF8 set?
- Find
 and
and  from the first
condition as in the case of PRF4 set.
from the first
condition as in the case of PRF4 set.
- And substitute these values in the last two
conditions and solve for
 and
and  . Thus we find
. Thus we find  , a member of PRF8 set.
, a member of PRF8 set.
- Find
 from the relation,
from the relation,  =
= 
- Find
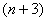 from the relation,
from the relation,
- Then find
 from the relation,
from the relation,

From the above procedure, we can find easily the members of PRF8 sets. Once we found out a PRF8 sets we can use equations (4.1) and (4.2) for decomposition of a signal of length  . The values of
. The values of 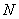 , in the above two equations, range from 1 to
, in the above two equations, range from 1 to  . The reconstruction of the original signal from the decomposed components can be done using equation (4.7) and (4.8) by substituting the numerator indices by
. The reconstruction of the original signal from the decomposed components can be done using equation (4.7) and (4.8) by substituting the numerator indices by  .
.
3. Filter of any even length N.
We have seen that any non-zero
real vector of length 2 can be used as member of PRF of length 2. For a
non-zero real vector of length 4, to be member of PRF of length 4, then the
vector has to satisfy one condition. For a non-zero real vector of length 6, to
be a member of a PRF set of length 6, it has to satisfy two conditions, for
length 8, three conditions and so on. That is the number of conditions to be
satisfied by a vector increases with the increase in the length of the vector
to be used as a filter. For a vector of
even length  , the number of conditions to be satisfied by it to be member of PRFN is
, the number of conditions to be satisfied by it to be member of PRFN is 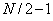 .
.
Let  be a non-zero real vector of even length
be a non-zero real vector of even length  . Then it has to satisfy the following
. Then it has to satisfy the following  conditions to be a member of PRF of length
conditions to be a member of PRF of length 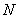 .
.
Member condition:
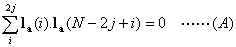

Where  and
and 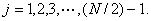
Equation (A) gives the general conditions to be satisfied by a non-zero vector of any even length 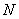 . From the conditions of equation (
. From the conditions of equation ( ), we can find a vector of real numbers of any even length by successively solving member condition equations as in previous sections.
), we can find a vector of real numbers of any even length by successively solving member condition equations as in previous sections.
Example-1: Generation of conditions to be satisfied by a vector of length 10.
Here 
When  , we get,
, we get,


 , first condition.
, first condition.
When  , we get the second condition as
, we get the second condition as

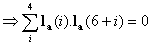
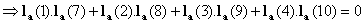 , second condition.
, second condition.
When  , we get the third condition as
, we get the third condition as


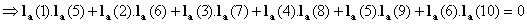 , third condition.
, third condition.
And when  , we get the fourth condition as
, we get the fourth condition as
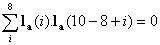

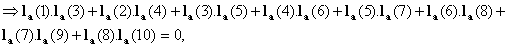
Fourth condition.
Thus from the above four
conditions, one can easily find a non-zero real vector of length 10, which will
be a member of PRF10 set. Once we obtain such a vector, then we can generate a
number of PRF sets of corresponding length by changing the signs or the
positions of the elements of the vector as in the previous section. Similarly
we can find various PRF sets of any higher lengths.
Once we find a PRFN set which
satisfies the above member condition, we can decompose the signal  as
as
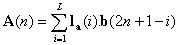
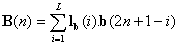
where 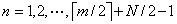 .
.
And the reconstruction can be done from the following two relations

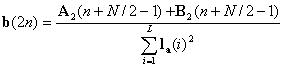
where ,
, 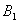 ,
,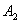 and
and  are obtained in the same way as in equations (4.3)-(4.6).
The above decomposition and the reconstruction formulas are for single level.
The formulas for decomposition can be used repeatedly for two or more levels.
When a signal is decomposed into two or more levels, then the reconstruction
formulas are used repeatedly beginning reconstruction from the components
decomposed last.
are obtained in the same way as in equations (4.3)-(4.6).
The above decomposition and the reconstruction formulas are for single level.
The formulas for decomposition can be used repeatedly for two or more levels.
When a signal is decomposed into two or more levels, then the reconstruction
formulas are used repeatedly beginning reconstruction from the components
decomposed last.
Let  be the length of each of decomposed
components in single level decomposition.
be the length of each of decomposed
components in single level decomposition.
i.e., 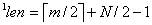 .
.
Then the length of a decomposed
component after  level decomposition
is given by
level decomposition
is given by
 , where
, where  denotes any integer
greater than equal to m. So a signal of length m is said to decomposable upto
level
denotes any integer
greater than equal to m. So a signal of length m is said to decomposable upto
level  using a filter of even length N if
using a filter of even length N if 
4. Discussion:
There is no hard and fixed rule that filters obtained from
the wavelets will always give good results. We also know that infinite number
of wavelets can be generated, which means that we can obtain infinite wavelet
filters. Thus what remains to us is to experiment with different filters and
find or choose the most suitable ones that will give best result for our
applications. Previously, finding the perfectly reconstructible filter
coefficients was itself a great problem. That is why most of the people use Db
wavelets or some established filter banks sets for different applications. But
now, finding the different sets of perfectly reconstructible filter (PRF) is
not a problem but a mere interesting fun. We don’t need to check whether a set
of real numbers can be a wavelet, nor does we need to check the admissibility
condition or the orthogonality condition. What we need is just to choose some
real numbers, which will satisfy equations of member condition of filter of
desired length.
We have given equations for member condition from which
one can find easily the PRF filter coefficients of choice. Those chosen filter
coefficients can be directly substituted in the equations for decomposition and
do the analysis. In none of the decomposition equations, extra process of down
sampling is required. And also no extra process of up sampling is required in
the reconstruction. Hence this feature can be made to improve the scheme of
decomposition and reconstruction in terms of computational speed. In other
words, the computational speed is doubly increased in our process of decomposition
and reconstruction than in that of filter bank scheme.
The decomposition and the reconstruction equations given
in the previous sections are only for single level decomposition. Multilevel
decomposition scheme can also be done as in multi-resolution analysis of
wavelet or pyramid decomposition of filter bank. And multi-channel
decomposition is possible as well but is somewhat different from that of filter
bank Moreover the same Db-wavelets filter-coefficients can be substituted in
the above decomposition and the reconstruction equation to get the same result,
as obtained from using wavelet. In other words, our approach is much more
generalized and those of orthogonal wavelets filters and filter banks cases.
5. Conclusion:
The criteria of obtaining PRF in
this case of ISITRA-1 (i.e., of QMF types), is much simpler than the ways of
obtaining PRF sets from wavelets. Choice of filter coefficients can be done in
many different ways. Once a filter is obtained, many different filters can be
configured from it, unlike in the case of wavelets filters and filter-banks,
which may be more suitable for different applications. Moreover, the
decomposition and reconstruction require less computational operations. It can
be applied in all areas of applications where the wavelets and filter banks are
used.
References:
- A. Croisier, D. Esteban & C. Galland, “Perfect
channel splitting by use of interpolation and decimation techniques”,
Proce. Int. Conf.on Information science and system, NJ, IEEE press, 1996.
- I.Daubechies, “Orthonormal bases of compactly
supported wavelets”, Comm. Pure and Appl. Math, vol-41, pp 906-966,1988.
- I. Daubechies, Ten Lectures on Wavelets,
Philadelphia, SIAM, 1992
- S. G. Mallat, “ A theory of multi-resolution signal
decomposition”, IEEE Trans. Pattern Anal. And Machine Intell., Vol-11, pp
674-693, 1989.
- Y.K. Singh & S.K. Parui, “Multiplication of two
multi-digit numbers using Bino’s Model of Multiplication”, Bulletin,
Calcutta Mathematical Society, submitted.
- Y.K Singh & S.K Parui, “On the level-n
Multiplication of 2 and 3-digit numbers using Bino’s Model of
Multiplication”, International Journal on Algebra and Computation,
submitted
- Y. K. Singh & S.K. Parui, “ISITRA, a better
alternative for signal decomposition and reconstruction”, Presented at ISMA-2001,
Feb.17-19, Saltlake City, Calcutta (INDIA).
Table-1 and Table-2.
Table-3.
My home page: Kirani Singh's Homepage
Also Visit:
center of points
Bino's Model of Multiplication
Any comment or suggestion is always welcome.
Y. Kirani Singh
email: kiranisingh@hotmail.com

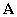 and
and 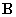 , not necessarily into an approximation and a detail.
Following the trend of ISITRA, we will denote the decomposition filters by
, not necessarily into an approximation and a detail.
Following the trend of ISITRA, we will denote the decomposition filters by  and
and 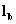 and the
reconstruction filters respectively by
and the
reconstruction filters respectively by 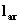 and
and  . The set of these four filters will be known as perfectly
reconstructible filter of length 2 (PRF2) set in the rest part of the paper.
. The set of these four filters will be known as perfectly
reconstructible filter of length 2 (PRF2) set in the rest part of the paper. be a discrete signal and
be a discrete signal and  and
and  , be any two decomposition filters of length 2, where
, be any two decomposition filters of length 2, where  and
and  are any two real
numbers. Then using Bino’s Model of Multiplication, we can write,
are any two real
numbers. Then using Bino’s Model of Multiplication, we can write,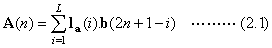
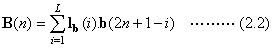
 is the length of the
filter and
is the length of the
filter and  .
. and
and  are the decomposed components of
are the decomposed components of 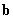
 and
and  as the reconstruction
filters. Finally, we can reconstruct back the original signal
as the reconstruction
filters. Finally, we can reconstruct back the original signal 

 then we find
then we find  or
or 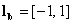 , according to step 2. And the corresponding reconstruction filters are
, according to step 2. And the corresponding reconstruction filters are  and
and  or
or 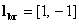 . Once we get the decomposition filters, we can use it for decomposing any signal using equations (2.1) and (2.2). And after some processing operations are done on the transformed data, they are used for reconstruction of the signal using the corresponding reconstruction filters.
. Once we get the decomposition filters, we can use it for decomposing any signal using equations (2.1) and (2.2). And after some processing operations are done on the transformed data, they are used for reconstruction of the signal using the corresponding reconstruction filters. ,
,  ,
,  and
and  .
.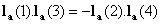
 satisfies the above two conditions, as the elements of
satisfies the above two conditions, as the elements of
 are not of same sign and
are not of same sign and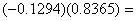 -0.1082
-0.1082 0.1082,
0.1082,  can be used for the
generation of the perfectly reconstructible filter set. The process of finding the other three filters of the set from
can be used for the
generation of the perfectly reconstructible filter set. The process of finding the other three filters of the set from  be a vector such that
be a vector such that  , then as usual we get,
, then as usual we get, 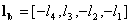
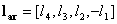 and
and 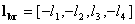 . These four filters are said to be QMF in terms of filter
bank and wavelets, but in our case these four filters are said to form a
perfectly reconstructible set. Once we get such a filter set, then we can decompose
a discrete signal,
. These four filters are said to be QMF in terms of filter
bank and wavelets, but in our case these four filters are said to form a
perfectly reconstructible set. Once we get such a filter set, then we can decompose
a discrete signal,

 is the length of the corresponding filter and
is the length of the corresponding filter and 
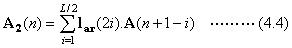

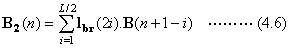

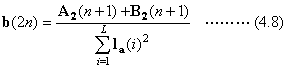
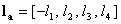 that satisfies the condition
that satisfies the condition 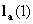 and
and  .
. , and then find
, and then find  from the relation
from the relation 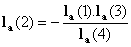 .
. =
= 
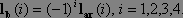

 be a vector of length 6. Then it should satisfy the following
two conditions to be member of perfectly reconstructible filter (PRF6) set.
be a vector of length 6. Then it should satisfy the following
two conditions to be member of perfectly reconstructible filter (PRF6) set.
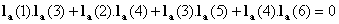
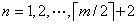 . And the original signal can be reconstructed from equations
(4.7) and (4.8) by substituting the denominator index by
. And the original signal can be reconstructed from equations
(4.7) and (4.8) by substituting the denominator index by 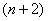 in place of
in place of  . Once a non-zero real vector for a filter is obtained, we
can find a number of PRF6 set from it by arranging the elements of the filter
in different ways. This flexibility is not mentioned in the case of wavelet
filters and filter banks.
. Once a non-zero real vector for a filter is obtained, we
can find a number of PRF6 set from it by arranging the elements of the filter
in different ways. This flexibility is not mentioned in the case of wavelet
filters and filter banks.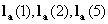 and
and  as finding a member of in PRF4 set.
as finding a member of in PRF4 set. and
and  for different values of
for different values of  . Thus we find
. Thus we find  , a member of PRF6 set.
, a member of PRF6 set. from the relation,
from the relation, 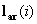 =
= 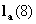
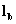 from the relation,
from the relation, 
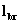 from the relation,
from the relation, 
 of length 8 to be a member of PRF8.
of length 8 to be a member of PRF8.


 and
and  from the first
condition as in the case of PRF4 set.
from the first
condition as in the case of PRF4 set. and
and  . Thus we find
. Thus we find  , a member of PRF8 set.
, a member of PRF8 set. from the relation,
from the relation,  =
= 
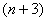 from the relation,
from the relation,
 from the relation,
from the relation,

 . The values of
. The values of 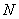 , in the above two equations, range from 1 to
, in the above two equations, range from 1 to  . The reconstruction of the original signal from the decomposed components can be done using equation (4.7) and (4.8) by substituting the numerator indices by
. The reconstruction of the original signal from the decomposed components can be done using equation (4.7) and (4.8) by substituting the numerator indices by  .
.  , the number of conditions to be satisfied by it to be member of PRFN is
, the number of conditions to be satisfied by it to be member of PRFN is 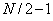 .
. be a non-zero real vector of even length
be a non-zero real vector of even length  . Then it has to satisfy the following
. Then it has to satisfy the following  conditions to be a member of PRF of length
conditions to be a member of PRF of length 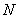 .
.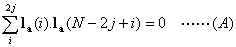

 and
and 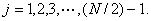
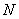 . From the conditions of equation (
. From the conditions of equation ( ), we can find a vector of real numbers of any even length by successively solving member condition equations as in previous sections.
), we can find a vector of real numbers of any even length by successively solving member condition equations as in previous sections. 
 , we get,
, we get, 

 , first condition.
, first condition. , we get the second condition as
, we get the second condition as
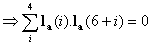
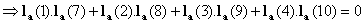 , second condition.
, second condition. , we get the third condition as
, we get the third condition as

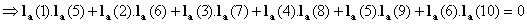 , third condition.
, third condition. , we get the fourth condition as
, we get the fourth condition as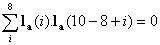

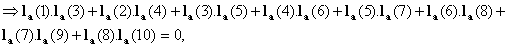
 as
as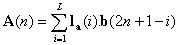
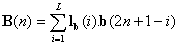
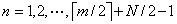 .
.
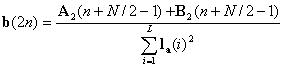
 ,
, 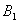 ,
,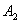 and
and  are obtained in the same way as in equations (4.3)-(4.6).
The above decomposition and the reconstruction formulas are for single level.
The formulas for decomposition can be used repeatedly for two or more levels.
When a signal is decomposed into two or more levels, then the reconstruction
formulas are used repeatedly beginning reconstruction from the components
decomposed last.
are obtained in the same way as in equations (4.3)-(4.6).
The above decomposition and the reconstruction formulas are for single level.
The formulas for decomposition can be used repeatedly for two or more levels.
When a signal is decomposed into two or more levels, then the reconstruction
formulas are used repeatedly beginning reconstruction from the components
decomposed last. be the length of each of decomposed
components in single level decomposition.
be the length of each of decomposed
components in single level decomposition. 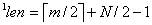 .
.  level decomposition
is given by
level decomposition
is given by , where
, where  denotes any integer
greater than equal to m. So a signal of length m is said to decomposable upto
level
denotes any integer
greater than equal to m. So a signal of length m is said to decomposable upto
level  using a filter of even length N if
using a filter of even length N if 
