Einfluss von Wind auf die Fahrzeit

Während eines Hollandurlaubes lernte ich die landestypischen Annehmlichkeiten für den Radfahrer kennen. Da wäre zum Beispiel der "fietspad". Mir blieben jedoch auch die landestypischen Unbilden nicht erspart. Zu ihnen zählt der Wind; eine gänzlich unangenehme Sache. Man könnte versucht sein, sich fröhlich zu reden. Schliesslich gibt es ja so etwas wie ausgleichende Gerechtigkeit. Fährt man das eine mal gegen den Wind, hat man das andere Mal den Wind im Rücken. Dann helfen bekanntlich ja alle Heiligen. Doch Obacht; so einfach ist das nicht. Nature is nonlinear.

Formal mit Formeln

Die Angelegenheit wollte ich nicht auf sich beruhen lassen. Also habe ich erst einmal eine formale Beschreibung des Problems angefertigt. Zugrunde liegt das folgende Modell. Es findet eine Fahrt von a nach b mit der Geschwindigkeit V_ab gegen den Wind mit der Windgeschwindigkeit V_w statt.

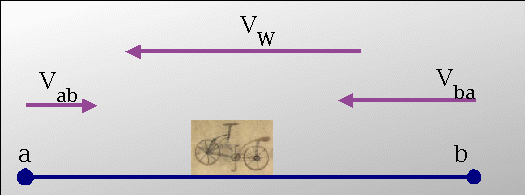
Anschliessend wird umgekehrt die gleiche Entfernung von b nach a, dieses mal jedoch mit Rückenwind und der Geschwindigkeit V_ba, zurückgelegt. Beide Wege werden mit der gleichen Anstrengung, also mit der gleichen Leistung

zurückgelegt. Darin ist F die Luftwiderstandskraft, A die angeströmte Querschnitt, c_w der Luftwiderstandsbeiwert und r die Luftdichte. Der Rollwiderstand wird hier vernachlässigt. Bei gleicher Leistung für Hin- und Rückweg gilt demnach:

Löst man diese kubische Gleichung nach V_ab auf, lässt sich mit einer angenommenen Windgeschwindigkeit und einer Fahr­ge­schwindig­keit mit dem Wind V_ba die Geschwindigkeit gegen den Wind V_ab berechnen.

Mit den nun bekannten Geschwindigkeiten ergibt sich die für den zurückgelegten Weg benötigte Zeit. Diese etwas unhandliche Lösung für V_ab lässt sich schwer interpretieren, jedoch einfach plotten. Für diejenigen, die andere Fälle plotten wollen, steht im Anhang die gnuplot Syntax:

Bildlich mit Bildern

Die folgende Darstellung zeigt die Abhängigkeit der Geschwindigkeit gegen den Wind von der Geschwindigkeit mit dem Wind und der Wind­geschwindigkeit V_ab = V_ab(V_ba, V_w).

Die rote Kurve zeigt den trivialen Fall ohne Wind; dann sind die Geschwindigkeiten für Hin- und Rückweg gleich. Die Geschwindigkeit gegen den Wind verschwindet in zwei Fällen.

1. Fährt man mit dem Wind genau mit der Windgeschwindigkeit, benötigt man keine Antriebsleistung; das ist gegen den Wind nur mit der Geschwindigkeit 0 zu bewerkstelligen.

2. Fährt man mit dem Wind garnicht, also mit der Geschwindigkeit 0, benötigt man ebenfalls keine Antriebsleistung; das ist gegen den Wind wiederum nur mit Tempo 0 zu bewerkstelligen.

Diese Fälle sind sicherlich nicht sonderlich praxisrelevant; interessant wird es, wenn die Fahrgeschwindigkeit deutlich grösser ist, als die Windgeschwindigkeit. Fährt man beispielsweise mit dem Wind mit 30km/h, kommt man bei einer Windgeschwindigkeit von 5km/h gegen den Wind bei gleicher Leistung nur auf ca. 23km/h. Wie sich diese Zusammenhänge auf die Gesamtfahrzeit auswirken, zeigt das folgende Bild. Dort ist das Verhältnis der Gesamtfahrtzeit für Hin- und Rückweg mit Wind zur Fahrzeit ohne Wind dargestellt.

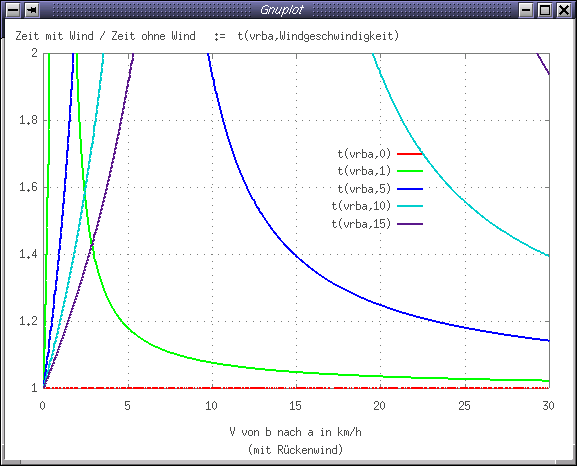
Ist die Windgeschwindigkeit V_w=0, ist das Zeitverhältnis 1 (rote Kurve). Lässt man sich nahezu vom Wind schieben, benötigt man nur sehr wenig Leistung. Mit dieser geringen Leistung kommt man gegen den Wind nur sehr langsam voran. Dann wird die Gesamtfahrzeit sehr gross. Mit anderen Worten; man nähert sich einer Singularität. Es sei nun ein etwas realistischerer Fall angenommen: Windgeschwindigkeit V_w=5km/h und Fahrgeschwindigkeit mit dem Wind V_ba=25km/h. Dann beträgt das Zeitverhältnis ca. 1.2. Es wird also knapp 20% mehr Zeit benötigt im Vergleich zu einer Fahrt ohne Wind.

Fazit

Man sieht also, dass bei konstanter Leistung nur ein Teil des Zeitverlustes bei Gegenwind auf dem Rückweg mit dem Wind ausgeglichen wird. Wollte man dennoch ohne Zeitverlust fahren, wäre das nur mit höherer Leistung und höherem Gesamtenergieaufwand möglich. (Diese, übrigens wesentlich einfachere Berechnung, sei dem geneigten Leser überlassen) Lassen sich nun die geschilderten Zusammenhänge praktisch nutzen? Die Hautpsätze der Thermodynamik lassen sich damit nicht überlisten; schneller voran kommt man mit dem Wissen also nicht. Wenn es an einem windigen Tag mal wieder nicht so recht voran gehen will, weiss man aber nun wenigstens warum.

Anhang

Gnuplot Syntax:

V_ab:

vrba(vrba,vw)= vw*-2.0/3.0+(vw**3*1.0/27.0+vrba**3*1.0/2.0-vw*vrba*vrba+1.0/2.0
         *vw*vw*vrba+sqrt(vrba**6*1.0/4.0-vw*vrba**5+1.0/27.0*vw**5*vrba+3.0/2.0
         *vw*vw*vrba**4-26.0/27.0*vw**3*vrba**3+19.0/108.0*vw**4*vrba*vrba))**(1.0/3.0)
         +(vw**3*1.0/27.0+vrba**3*1.0/2.0-vw*vrba*vrba+1.0/2.0*vw*vw*vrba
         -sqrt(vrba**6*1.0/4.0-vw*vrba**5+1.0/27.0*vw**5*vrba+3.0/2.0
         *vw*vw*vrba**4-26.0/27.0*vw**3*vrba**3+19.0/108.0*vw**4*vrba*vrba))**(1.0/3.0) 

Zeitverhältnis:

t(vrba,vw)=(1+vrba/f(vrba,vw))/2.0
           vrab(vrba,vw)= vw*-2.0/3.0+(vw**3*1.0/27.0+vrba**3*1.0/2.0
           -vw*vrba*vrba+1.0/2.0*vw*vw*vrba+sqrt(vrba**6*1.0/4.0-vw*vrba**5
           +1.0/27.0*vw**5*vrba+3.0/2.0*vw*vw*vrba**4-26.0/27.0*vw**3*vrba**3
           +19.0/108.0*vw**4*vrba*vrba))**(1.0/3.0)+(vw**3*1.0/27.0+vrba**3
           *1.0/2.0-vw*vrba*vrba+1.0/2.0*vw*vw*vrba-sqrt(vrba**6*1.0/4.0
           -vw*vrba**5+1.0/27.0*vw**5*vrba+3.0/2.0*vw*vw*vrba**4-26.0/27.0
           *vw**3*vrba**3+19.0/108.0*vw**4*vrba*vrba))**(1.0/3.0)