![]()
Visualizar gráficos y tablas del Método Simplex
La solución de un modelo de optimización está organizada en el explorador de soluciones o Mapa de Solución.
Por ejemplo, para el siguiente modelo:
Z=3x+y+u
x+2y+3u<=10
5x+9y+7u<=15
2x+y-u>=8
3x+2y+u=12
la ventana tiene el siguiente aspecto:

Los items de esta ventana exploradora contienen la información de los elementos del proceso de solución y del análisis sensitivo. Para observar los resultados cuando ejecute el programa fuera de este tutorial se hace clic sobre uno de ellos.
En los siguientes items, se explican las propiedades de cada uno de los elementos de esta ventana:
![]()
Después de hacer clic sobre el item Tabla Simplex surge una Tabla de Datos del modelo estándar conformando un Sistema Lineal con la variable objetiva Z, y ordenadamente las variables de decisión, las variables de holgura por deficiencia ( letras H numeradas según el orden de la restricción £ ), las variables de exceso ( letras E numeradas según el orden de la restricción con ³ ), y las variables artificiales ( letras A numeradas en los casos de = o de ³ ). Por ejemplo:
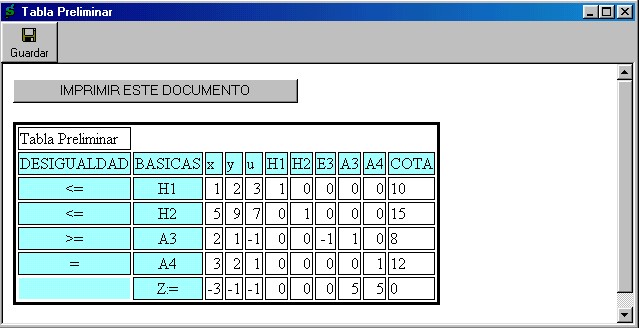
Los signos de relación de cada restricción aparecen en la primera columna titulada Desigualdades o Ecuaciones. Las variables Básicas quedan en la segunda columna. En la primera fila se ordenan todas las variables, y bajo cada una de ellas se dispone la columna de datos. La columna final indicada con B corresponde a los términos constantes o independientes del sistema lineal de ecuaciones del modelo estándar.
La última fila se reserva para los coeficientes de la función objetivo, en la última casilla aparece el valor de Z que inicia desde cero y cambiará de valor en cada nueva Tabla hasta llegar al valor óptimo salvo división entre el valor del Pivote.
![]()
Para obtener resultados finales desde la ventana Mapa de solución, primero despliegue el contenido de la carpeta Soluciones, y luego haga clic sobre el item solución; de allí surgirá un sombreado resaltando la cantidad total de iteraciones cuando exista alguna solución. En el evento de resultar insoluble el modelo debido a los casos de no acotamiento de la función objetivo, esta ventana mostrará el aviso correspondiente; pero en los casos de resultar soluciones alternativas e infinitas soluciones para las variables de decisión será desplegada la opción de cálculo paramétrico.

Con otro clic muestra resultados y cuadros con las soluciones completas. El análisis de sensitividad de las variables del modelo aparece en los recuadros de Variación , y bajo ellos los respectivos valores extremos de la función objetivo; en los casos de intervalos infinitos se advierte la no existencia de cotas extremas. A continuación se ilustran los resultados de un modelo ejemplar:
Solución Optima: Z = 360000
*** SOLUCION PARA VARIABLES DE DECISION BASICAS ***
| Variable | Variación | |
| y=18000 | 20 <= C2 = 20 <=Sin Cota Superior | |
| Z Mínimo = 360000 | Sin Z Máximo | |
*** VARIABLES DE DECISION NO BASICAS ***
| Variable | Variación | |
| x=0
ALTERNATIVA BASICA |
Sin Cota Inferior<=C1 = 0 <=Sin Cota Superior | |
| Costo Reducido = 0 | ||
*** SOLUCION PARA COTAS DE RESTRICCION BASICAS ***
| Holgura o Excedente | Variación | |
| H1=200 | 900 <= B1 = 1100<=Sin Cota Superior | |
| Z Mínimo = 0 | Sin Z Máximo | |
| H3=1100 | 900 <= B3 = 2000<=Sin Cota Superior | |
| Z Mínimo = 0 | Sin Z Máximo | |
*** SOLUCION PARA COTAS DE RESTRICCION NO BASICAS ***
| Holgura o Excedente | Variación | |
| H2=200 | 0 <= B2 = 0<=2200 | |
| Precio Dual = 200 | ||
El análisis sensitivo llega hasta los márgenes de variación de cada coeficiente de la función objetivo y de cada una de las cotas de restricción originales del modelo.
En caso de no existir un valor extremo o margen del intervalo de sensitividad, entonces se afirmará la ausencia de la cota superior o de la cota inferior para el respectivo coeficiente o parámetro.
Note que además de los márgenes de sensitividad para cada coeficiente de la función objetivo, aparece el Costo Reducido que indica en cuánto debe ajustarse dicho coeficiente para que la variable respectiva ingrese a la Base de Soluciones, es decir se convierta en Básica.
En el caso de los parámetros de acotamiento, el análisis expresa el Precio Dual del insumo como la Tasa de Impacto en la función objetivo según el cambio unitario del recurso correspondiente.
Cómodamente se adelanta o retrocede la página de resultados para visualizar cada Tabla del proceso Simplex.
| ITERACION Nº 1 | |||||||
| DESIGUALDAD | BASICAS | x | y | H1 | H2 | H3 | COTA |
| <= | H1 | 0,05 | 0,05 | 1 | 0 | 0 | 1100 |
| <= | H2 | 0,05 | 0,1 | 0 | 1 | 0 | 1800 |
| <= | H3 | 0,1 | 0,05 | 0 | 0 | 1 | 2000 |
| MAX |
Z:= |
-10 |
-20 |
0 |
0 |
0 |
0 |
En la siguiente tabla se observa además la coloreación tanto de la fila como de la columna cuya intersección coordenada nos muestra al futuro elemento Pivote :
| ITERACION Nº 2 | |||||||
| Variable Entrante : y | Variable Saliente : H2 | ||||||
| DESIGUALDAD | BASICAS | x | y | H1 | H2 | H3 | COTA |
| <= | H1 | 0,025 | 0 | 1 | -0,5 | 0 | 200 |
| <= | y | 0,5 | 1 | 0 | 10 | 0 | 18000 |
| <= | H3 | 0,075 | 0 | 0 | -0,5 | 1 | 1100 |
| MAX | Z:= | 0 | 0 | 0 | 200 | 0 | 360000 |
De este modo será sencillo reconocer el proceso de eliminación sistemática Gauss - Jordan necesario para obtener la siguiente iteración de la Tabla.
![]()
Si el problema tiene infinitas soluciones, Simplex2000 muestra la forma paramétrica que identifica a cada solución. Cuando ejecute el programa y desee visualizar algunas de las infinitas soluciones solo tendrá que hacer clic en el item correspondiente. Por ejemplo:

En este caso la ventana de las soluciones paramétricas tiene el aspecto :
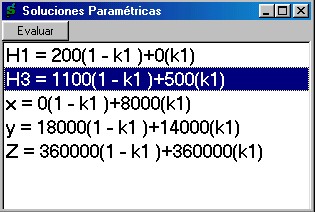
Note que las variables involucradas en la parametrización son expresadas en términos del parámetro numerado k1 ( existen casos de modelos cuyas soluciones incluyen varios parámetros ).
Si desea obtener alguna solución particular, seleccione la ecuación paramétrica y luego haga clic en evaluar. En seguida aparecerá un cuadro de solución como el siguiente:

Ahora, simplemente asígnele al parámetro k algunos valores específicos dentro del intervalo real que va desde cero hasta uno; basta seleccionar el parámetro de la lista de la izquierda y arrastrarlo a lo largo de la cremallera.
![]()
Configuración del método de solución
Durante la ejecución, a veces es deseable cambiar el valor
de la constante M utilizada en el método de Penalización o modificar
algunas opciones de desarrollo en los casos de empates múltiples; para hacerlo
basta hacer clic en el botón de llave
![]() con el cual aparece el
siguiente formulario:
con el cual aparece el
siguiente formulario:

Para solucionar modelos con muchas variables (10 o más) es recomendable desactivar los items : Mostrar iteraciones, Encontrar Optimos alternativos , y Mostrar la variación de Z en cotas de restricción. ; de lo contrario el programa tardará en mostrar la solución.
Note que mientras no se cambien estas instrucciones, el programa ejecutará de modo predeterminado según las indicaciones señaladas por el punto de la respectiva viñeta. Es conveniente para el auto- aprendizaje aplicar modelos que tengan todas las opciones posibles y ejecutarlas cada vez con un método distinto; esto es con el fin de comparar la efectividad entre todos ellos. Existen sin embargo algunos modelos de redes que ofrecen múltiples opciones para las variables de decisión, ello no debe preocupar pués dependen de la solución de los empates entre las variables No Básicas que resultan con coeficiente cero en la fila de la función objetivo; a éstas variables Degeneradas se les da un tratamiento correspondiente.